Oficina
Somas e diferenças
| Cosseno da diferença | Seno da diferença |
 |
Discutiremos nesta sala mais quatro propriedades da trigonometria do triângulo retângulo. |
| Cosseno da soma | Seno da soma |
Cosseno da diferença
[tex]\qquad cos \, (\alpha-\beta)=cos \, \alpha\cdot cos \, \beta+sen \, \alpha\cdot sen \, \beta \, .[/tex]
Justificativa
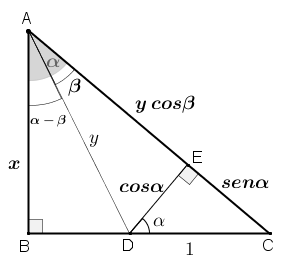
A princípio, observem a Figura 1 e tentem obter a igualdade proposta:
[tex]\qquad\qquad cos \, (\alpha-\beta)=cos \, \alpha\cdot cos \, \beta+sen \, \alpha\cdot sen \, \beta \, [/tex].
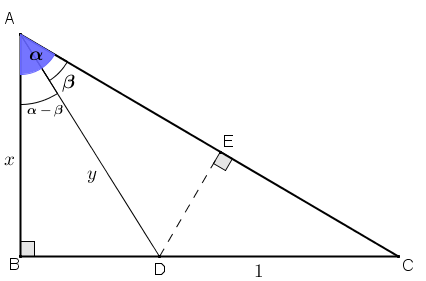
Figura 1
● o triângulo [tex]ABC[/tex] é retângulo em [tex]B[/tex];
● o triângulo [tex]CED[/tex] é retângulo em [tex]E[/tex];
● o segmento [tex]DC[/tex] é unitário;
● o comprimento do segmento [tex]AB[/tex] é [tex]x[/tex];
● o comprimento do segmento [tex]AD[/tex] é [tex]y[/tex].
– Não conseguiram?
➤ Não faz mal; tentem a dica abaixo.
– Não conseguiram determinar os comprimentos?
➤ Mais uma dica…
– Nada ainda????
➤ Hora do applet!
Agora é com vocês!
Que tal vocês tentarem concluir a justificativa?
Conferindo…
Para conferir o trabalho realizado, cliquem no botão!
Seno da diferença
[tex]\qquad sen \, (\alpha-\beta)=sen \, \alpha\cdot cos \, \beta-sen \, \beta\cdot cos \, \alpha \, .[/tex]
Justificativa
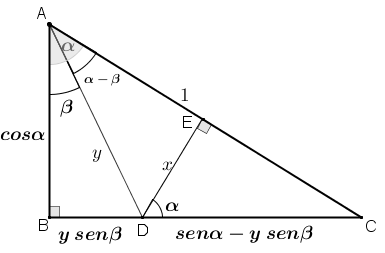
A partir da Figura 2, tentem obter a igualdade proposta:
[tex]\qquad\qquad sen \, (\alpha-\beta)=sen \, \alpha\cdot cos \, \beta-sen \, \beta\cdot cos \, \alpha \, [/tex].
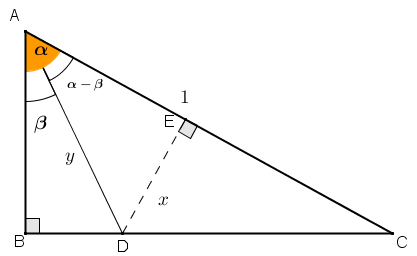
Figura 2
● o triângulo [tex]ABC[/tex] é retângulo em [tex]B[/tex];
● o triângulo [tex]CED[/tex] é retângulo em [tex]E[/tex];
● o segmento [tex]AC[/tex] é unitário;
● o comprimento do segmento [tex]DE[/tex] é [tex]x[/tex];
● o comprimento do segmento [tex]AD[/tex] é [tex]y[/tex].
– Não deu certo?
➤ Não faz mal; lá vai a primeira dica.
– Tá, conseguiram os comprimentos mas não conseguem progredir?
➤ Aí vai outra dica…
– Nada ????
➤Hora do applet!
Agora é com vocês!
Que tal concluírem essa justificativa?
Conferindo…
Para conferir o trabalho realizado, cliquem no botão!
Cosseno da soma
[tex]\qquad cos \, (\alpha+\beta)=cos \, \alpha\cdot cos \, \beta-sen \, \alpha\cdot sen \, \beta \,.[/tex]
Justificativa
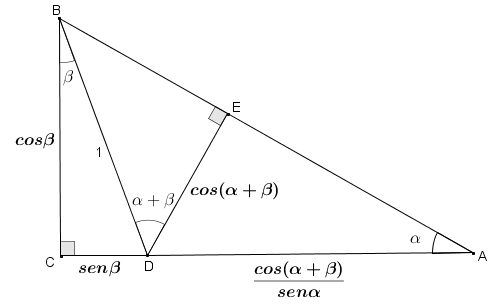
A partir da Figura 3, tentem obter que:
[tex]\qquad\qquad cos \, (\alpha+\beta)=cos \, \alpha\cdot cos \, \beta-sen \, \alpha\cdot sen \, \beta \,. [/tex]
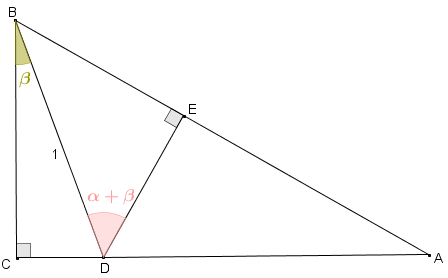
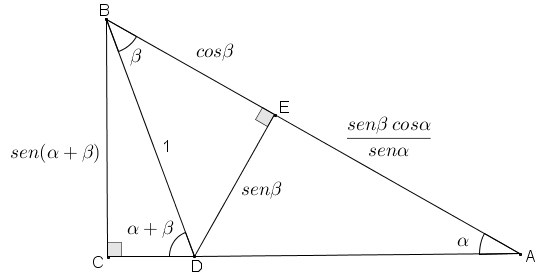
Figura 3
● o triângulo [tex]BCA[/tex] é retângulo em [tex]C[/tex];
● o triângulo [tex]BED[/tex] é retângulo em [tex]E[/tex];
● o triângulo [tex]BCD[/tex] é retângulo em [tex]C[/tex];
● o segmento [tex]BD[/tex] é unitário.
– Estão confusos?
➤ Calma, aí vai a primeira dica.
– E aí, mais uma ajuda?
➤ Lá vai outra dica…
– Nada ????
➤Hora do applet!
Agora é com vocês!
Concluam mais esta justificativa!
Conferindo…
Para conferir o trabalho realizado, cliquem no botão!
Seno da soma
[tex]\qquad sen \, (\alpha+\beta)=sen \, \alpha\cdot cos \, \beta+sen \, \beta\cdot cos \, \alpha [/tex].
Justificativa
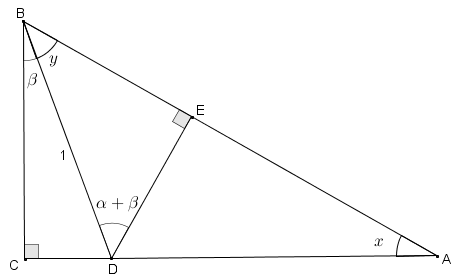
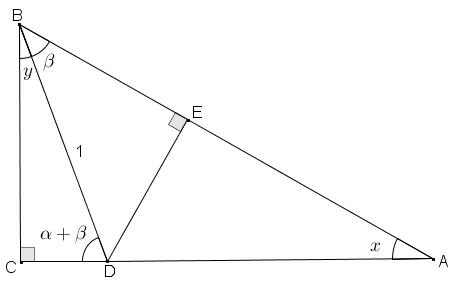
A partir da Figura 4, tentem obter que:
[tex]\qquad\qquad sen \, (\alpha+\beta)=sen \, \alpha\cdot cos \, \beta+sen \, \beta\cdot cos \, \alpha[/tex].
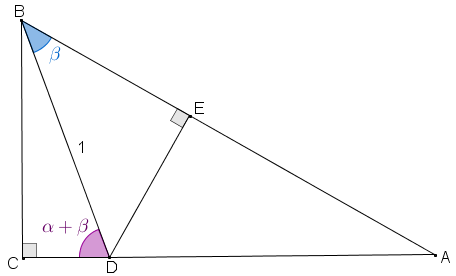
Figura 4
● o triângulo [tex]BCA[/tex] é retângulo em [tex]C[/tex];
● o triângulo [tex]BED[/tex] é retângulo em [tex]E[/tex];
● o triângulo [tex]BCD[/tex] é retângulo em [tex]C[/tex];
● o segmento [tex]BD[/tex] é unitário.
– Não deu certo?
➤ Normal; vejam a primeira dica.
– Conseguiram os comprimentos e não sabem como prosseguir?
➤ Olhem a Dica 2 …
– É, a coisa não é simples mesmo. Então…
➤Hora do applet!
Vamos concluir a justificativa?
Agora é com vocês!
Conferindo…
Para conferir o trabalho realizado, cliquem no botão!
Equipe COM – OBMEP
✓ ROGER, B. N., Proofs Without Words – Exercises in Visual Thinking. The Mathematical Association of America, 1993.
✓ ROGER, B. N., Proofs Without Words II – More Exercises in Visual Thinking. The Mathematical Association of America, 2000.
✓ WAGNER, E,; MORGADO, A. C. O.; DO CARMO, M. P., Trigonometria e Números Complexos. Rio de Janeiro: SBM, 2005.