Um pouco sobre divisibilidade
Parte 1 – Múltiplos e divisores
 |
O comportamento de observar relações, criar e descrever padrões visando generalizações é muito bem-vindo no estudo da Matemática! |
 |
Vamos, inicialmente, formalizar dois objetos matemáticos com os quais vocês estão habituados a trabalhar: múltiplos e divisores. |
Múltiplos e divisores
Números podem estar relacionados entre si ou formar sequências numéricas com particularidades interessantes. Essas particularidades são comumente conhecidas por padrões ou regularidades. Aqueles que gostam de resolver problemas de matemática com certeza já se depararam com questões interessantes envolvendo a descoberta de regularidades em determinadas sequências de números, ou seja, questões nas quais é necessário procurar uma lei geral que caracterize todo e qualquer elemento de uma dada sequência numérica.
O nosso ponto de partida para o estudo da divisibilidade será exatamente a procura de padrões e regularidades em algumas sequências formadas por números naturais. Não serão sequências mirabolantes, mas sequências que permitirão que desenvolvamos um pedacinho importante da teoria dos números naturais. Apresentamos três delas:
- Sequência 1: 0 , 2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , …
- Sequência 2: 0 , 5 , 10 , 15 , 20 , 25 , 30 , 35 , 40 , …
- Sequência 3: 0 , 10 , 20 , 30 , 40 , 50 , 60 , 70 , 80 , …
O que têm em comum os elementos da primeira sequência? O que há de especial nos elementos da segunda sequência? Que elementos vêm após o 80 na terceira sequência?
Podemos responder facilmente a essas três perguntas se observarmos que as sequências foram obtidas multiplicando-se cada número natural por 2, 5 e 10, respectivamente. Com isso podemos reescrever as sequências da seguinte forma:
- Sequência 1: 0 × 2, 1 × 2, 2 × 2, 3 × 2, 4 × 2, 5 × 2, 6 × 2, 7 × 2, 8 × 2, …
- Sequência 2: 0 × 5, 1 × 5, 2 × 5, 3 × 5, 4 × 5, 5 × 5, 6 × 5, 7 × 5, 8 × 5, …
- Sequência 3: 0 × 10, 1 × 10, 2 × 10, 3 × 10, 4 × 10, 5 × 10, 6 × 10, 7 × 10, 8 × 10, …
e como multiplicamos números naturais por 2, 5 e 10, dizemos que as sequências são, respectivamente, formadas por:
- múltiplos de 2;
- múltiplos de 5;
- múltiplos de 10.
O padrão que caracteriza os elementos de qualquer uma dessas três sequências (e responde, particularmente, às três perguntas formuladas) pode ser generalizado. Podemos, então, produzir para cada número natural [tex] a[/tex] a sequência dos múltiplos de [tex] a[/tex]:
- [tex] \, \, 0 \times a, \, 1 \times a, \, 2 \times a, \, 3 \times a, \, 4 \times a, \, 5 \times a, \, 6 \times a, \, 7 \times a, \, 8 \times a, \, \cdots[/tex].
Feitos os produtos, podemos notar que nessa sequência o primeiro elemento é [tex] 0[/tex] e cada elemento, a partir do segundo, é a soma entre o elemento anterior e [tex] a[/tex], ou seja, é uma sequência de números que se inicia em zero e vai aumentando de [tex] a[/tex] em [tex] a[/tex]:
- [tex] \, \, 0, \, \, a, \, \, 2a, \, \, 3a, \, \, 4a, \, \, 5a, \, \, 6a, \, \, 7a, \, \, 8a, \, \, \cdots[/tex].
A relação entre cada elemento dessa sequência e o número natural [tex] a[/tex] que a definiu será importante para os nossos propósitos, portanto vamos registrá-la como uma definição.
Dessa forma:
- 18 é múltiplo de 2, pois 18 = 9 × 2 e 9 é um número natural;
- 40 é múltiplo de 10, pois 40 = 4 × 10 e 4 é um número natural;
- 259 é múltiplo de 37, pois 259 = 7 × 37 e 7 é um número natural;
- 15 não é múltiplo de 7, pois não existe um número natural [tex]k[/tex] tal que [tex]15=k\times 7[/tex];
- o único múltiplo de 0 é o próprio 0, já que [tex]k \times 0=0[/tex] para qualquer número natural [tex]k[/tex];
- no entanto, 0 é múltiplo de qualquer número natural [tex]a[/tex], pois [tex]0=0 \times a[/tex].
(Observe que 0 × 7 = 0, 1 × 7 = 7, 2 × 7 = 14 . Agora, 3 × 7 e todos os demais produtos [tex]k \times 7[/tex] serão maiores do que 15.)
Observação: Na definição acima, a exigência de que [tex]k[/tex] seja um número natural é para evitar, por exemplo, que alguém classifique [tex]20[/tex] como um múltiplo de [tex]9[/tex], já que [tex]20=\dfrac{20}{9}\times 9[/tex]. Nesse caso, [tex]20=k\times 9[/tex], mas [tex]k[/tex] não é um número natural.
|
O nome é bem razoável – um múltiplo é um número obtido como resultado de uma multiplicação . . . |
 |
 |
Isso mesmo! |
|
Então, para sabermos se um número natural [tex]n[/tex] é múltiplo de um número natural [tex]a[/tex], basta ir multiplicando os números naturais, em ordem crescente, por [tex]a[/tex] para tentarmos obter [tex]n[/tex] como um dos possíveis produtos. |
 |
 |
Teoricamente você está correto. |
|
E agora ?????? |
 |
 |
Nada muito desesperador . . . |
Múltiplos sem multiplicações
Vamos dividir a nossa discussão de como “procurar múltiplos sem fazer multiplicações” em duas partes.
Para essa discussão, vamos considerar que não procuraremos múltiplos para zero, pois já observamos que o único múltiplo de zero é o próprio zero.
Parte 1
Sejam [tex]n[/tex] e [tex]a[/tex] números naturais, com [tex]a\ne 0[/tex], tais que [tex]n[/tex] é um múltiplo de [tex]a[/tex].
Nesse caso, o que acontece com o quociente e o resto da divisão de [tex]n[/tex] por [tex]a[/tex]?
Observemos…
| [tex]\qquad \qquad \begin{array}{r} n \, \end{array} \begin{array}{|r} \, a \, \, \\ \hline \end{array}[/tex] [tex]\qquad \qquad\begin{array}{r} r \end{array}\begin{array}{r} \, \, \, \, q \end{array}[/tex] |
Ao dividirmos [tex]n[/tex] por [tex]a[/tex] encontraremos um quociente [tex]q [/tex] e um resto [tex]r [/tex], únicos, tais que: [tex]\quad (1) \, \, 0 \le r \lt a \qquad \qquad [/tex] [tex](2) \, \, n=q \times a+r[/tex]. |
Mas [tex]n[/tex] é um múltiplo de [tex]a[/tex], logo existe um número natural [tex]k[/tex] tal que [tex]n=k\times a[/tex], ou seja, [tex]n=k\times a+0[/tex].
Assim temos [tex]n=k\times a+0[/tex] e queremos [tex]n=q \times a+r[/tex].
Como [tex]q[/tex] e [tex]r[/tex] são únicos, necessariamente teremos [tex]\fcolorbox{black}{#CDC9C9}{$q=k$}[/tex] , [tex]\fcolorbox{black}{#CDC9C9}{$r=0$}[/tex] e, então,
| [tex]n[/tex] | [tex]a[/tex] |
| [tex]0 [/tex] | [tex]k[/tex] |
Podemos, portanto, concluir que:
Se [tex]n[/tex] é um múltiplo de [tex]a[/tex] e [tex]a\ne 0[/tex], então o resto da divisão de [tex]n[/tex] por [tex]a[/tex] é zero.[tex]\qquad \qquad(i)[/tex]
Parte 2
Suponhamos, agora, que [tex]n[/tex] e [tex]a[/tex] sejam números naturais, com [tex]a\ne 0[/tex], tais que a divisão de [tex]n[/tex] por [tex]a[/tex] seja exata.
| [tex]n[/tex] | [tex]a[/tex] |
| [tex]0 [/tex] | [tex]q[/tex] |
Como em uma divisão o dividendo é a soma entre o resto e o produto do divisor pelo quociente, então temos que [tex]n=q\times a+0[/tex], ou seja, [tex]n=q\times a[/tex]. Como [tex]n=q\times a[/tex] e [tex]q[/tex] é natural, temos que [tex]n[/tex] é múltiplo de [tex]a[/tex].
Pelo exposto, podemos concluir que
Se a divisão de [tex]n[/tex] por [tex]a[/tex] tem resto zero, então [tex]n[/tex] é um múltiplo de [tex]a[/tex].[tex]\qquad \qquad(ii)[/tex]
As conclusões [tex](i)[/tex] e [tex](ii)[/tex] podem ser escritas de uma só vez, da seguinte forma:
Se [tex]n[/tex] e [tex]a[/tex] são números naturais, com [tex]a\ne 0[/tex], então
[tex]n[/tex] é um múltiplo de [tex]a[/tex] se, e somente se, a divisão de [tex]n[/tex] por [tex]a[/tex] for exata.
|
Então, para saber se um número é múltiplo de outro fazemos várias multiplicações ou apenas uma divisão. |
 |
 |
Quase isso! |
|
Que bom que teremos outras alternativas. |
 |
 |
Precisaremos desenvolver um pouco mais de teoria para estabelecer esses outros métodos. Por agora, vamos aproveitar a discussão e apresentar mais uma maneira de nos referirmos a dois números naturais tais que um é múltiplo do outro. |
Já sabemos que, nesse caso, dizemos, também, que [tex]m[/tex] é um múltiplo de [tex]d[/tex].
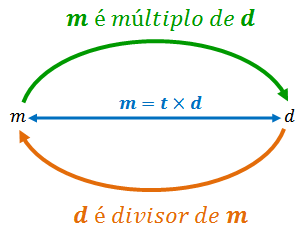
Nomenclaturas
Observem que quase toda a discussão do tópico anterior pode ser feita a partir da divisão de um número natural [tex]a[/tex], por um número natural não nulo [tex]b[/tex].
| [tex]a \, \, \, \, [/tex] | [tex] \, \, \, \, b[/tex] |
| [tex]r [/tex] | [tex]\quad q \quad[/tex] |
Em particular, se [tex]r=0[/tex], temos que [tex]a=q\times b[/tex] e podemos relacionar os números [tex]a[/tex] e [tex]b[/tex] dizendo que:
- a divisão de [tex]a[/tex] por [tex]b[/tex] tem resto [tex]0[/tex];
- a divisão de [tex]a[/tex] por [tex]b[/tex] é exata;
- [tex]a[/tex] é divisível por [tex]b[/tex];
- [tex]b[/tex] é um divisor de [tex]a[/tex];
- [tex]a[/tex] é um múltiplo de [tex]b[/tex].
(Cinco nomenclaturas para designar o mesmo fato: [tex]a=q\times b[/tex], com [tex]a[/tex], [tex]b[/tex], [tex]q[/tex] números naturais e [tex]b\ne 0[/tex].)
Observações:
1) É importante ter em mente que, ao iniciarmos uma divisão, estamos assumindo que essa divisão pode ser realizada e, portanto, o divisor é diferente de zero.
| [tex]Dividendo \, \, \, \, [/tex] | [tex] \, \, \, \, divisor[/tex] |
| [tex]resto [/tex] | [tex]\quad quociente \quad [/tex] |
No entanto observem, mais uma vez, que essa restrição não tira a generalidade da discussão, uma vez que, se zero é divisor de [tex]a[/tex], então existe um natural [tex]t[/tex] de forma que [tex]a=t\times 0 [/tex] e com isso, necessariamente, [tex]a=0[/tex].
2) Pelo anteriormente exposto, ao executarmos uma divisão assumiremos que o número utilizado como divisor é diferente de zero, mesmo que isso não seja explicitamente dito.
3) Nesta nossa discussão, denotaremos o produto do número [tex]m[/tex] pelo número [tex]n[/tex] também por [tex]m\cdot n[/tex] ou simplesmente por [tex]mn[/tex].
 |
A partir dos conceitos de múltiplo e divisor, podemos obter algumas classificações interessantes para os números naturais. Alguns desses números serão objetos de Salas de Estudo específicas, mas vale a pena defini-los aqui e aproveitar para amadurecer um pouco mais os conceitos de múltiplo e de divisor. Além do que, esses números são temas frequentes de problemas de várias olimpíadas. |
Alguns números especiais
Neste tópico serão apresentados alguns números especiais que foram criados a partir da mistura entre misticismo e matemática, tão peculiar aos gregos antigos. Particularmente, os pitagóricos ficaram conhecidos por sua adoração aos números, inclusive baseando neles a sua filosofia e o seu modo de viver; e é aos pitagóricos que se atribui a descoberta de propriedades interessantes e curiosas sobre os números especiais que aqui apresentaremos. O que se pode afirmar com certeza é que propriedades envolvendo esses números já apareciam, há cerca de 300 anos a.C., nos Elementos de Euclides, nos três livros dedicados à Aritmética: o livro VII, o livro VIII e o livro IX.
Lidar na prática com esses números pode não ser uma tarefa fácil, já que eles são definidos a partir dos conceitos de divisor e múltiplo. Mas eles aparecem em belíssimos problemas criados ao longo da história da matemática!
Vamos conhecer alguns desses números?
Basta clicar no respectivo botão!
 |
Agora vocês já tem material suficiente para trabalhar, não é? |
|
Vamos lá, pessoal! |

|
Atividades
Para executar as atividades que serão propostas, vocês precisarão apenas das definições de:
- múltiplo e divisor;
- números pares e números ímpares;
- números perfeitos, números abundantes, números deficientes e números quase perfeitos;
- números primos e números compostos.
Utilizem inicialmente os applets para fixar os conceitos de divisor e múltiplo e depois ataquem os problemas!
Bons estudos!
Boa diversão!!!
 |
Conheçam a continuação desta sala clicando AQUI |
Equipe COM – OBMEP
Março de 2016.
✓ BOYER, C. B., História da Matemática. São Paulo: Edgard Blücher, 1974.
✓ DANTZIG, T., Número: A linguagem da Ciência. Rio de Janeiro: Zahar Editores, 1970.
✓ DOMINGUES, H. H., Fundamentos de Aritmética. São Paulo: Atual Editora, 1991.
✓ HOWARD, R., Introdução à História da Matemática. Campinas: Editora Unicamp, 2004.
✓ RIBENBOIM, P., Números Primos: mistérios e recordes. Coleção Matemática Universitária. Rio de Janeiro: IMPA, 2001.
✓ SAMPAIO, J.C.V.; CAETANO, P.A.S., Introdução à Teoria dos Números – Um curso breve. São Carlos: EDUFScar, 2008.

