Segredos do Triângulo de Pascal
Segredos 11, 12 e 13
O Segredo 11 envolve os números conhecidos como Quadrados perfeitos.
- Definição: Quadrado perfeito é qualquer número natural que pode ser escrito como o quadrado de um número também natural.
Para quem está habituado a uma linguagem mais matemática, um número natural [tex]n[/tex] é dito um quadrado perfeito, se, e somente se, existir um número natural [tex]a[/tex] tal que [tex]n=a^2[/tex].
(Para aprender um pouco mais sobre Quadrados Perfeitos, visite esta Sala do nosso Blog.)
A partir das duas representações do Triângulo de Pascal mostradas abaixo, vamos fazer algumas somas para ilustrar este segredo:
[tex]\qquad 1+3=4=2^2\\
\qquad 3+6=9=3^3\\
\qquad 6+10=16=4^2\\
\qquad 10+15=25=5^2\\
\qquad 15+21=36=6^6\\
\qquad 21+28=49=7^2\\
\qquad 28+36=64=8^2\\
\qquad 36+45=81=9^2.[/tex]
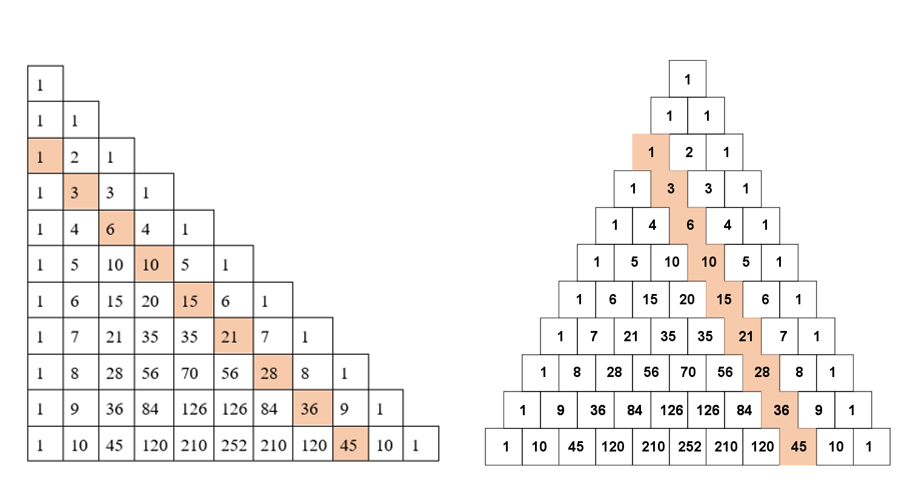
Segredo 11: Se somarmos duas entradas consecutivas quaisquer da terceira diagonal do Triângulo de Pascal, obtemos um número quadrado perfeito.
A propriedade do segredo seguinte é conhecida como Taco de Hockey ou Teorema das Diagonais.
 Imagem extraída de Freepik
Imagem extraída de Freepik
Vejam alguns exemplos para entenderem o nome da propriedade!
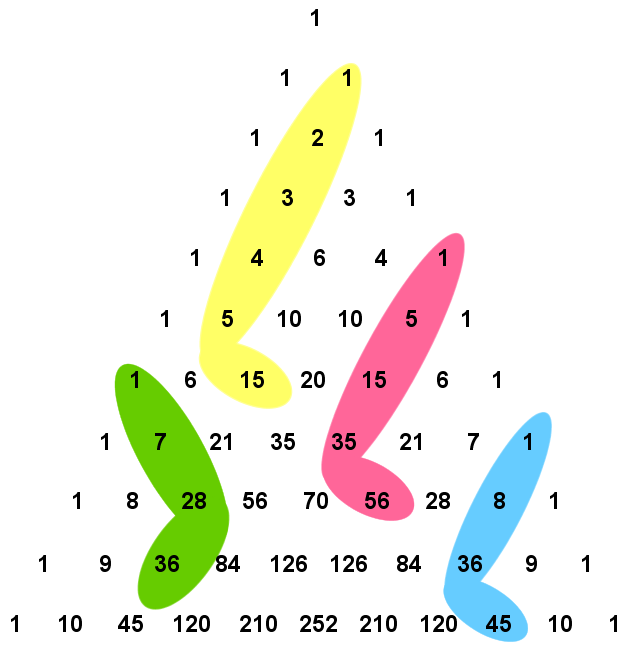
Segredo 12: Se somarmos os [tex]k[/tex] primeiros elementos de qualquer diagonal de um Triângulo de Pascal na forma de triângulo isósceles, obtemos o número que se encontra abaixo do último elemento, mas na diagonal contrária.
(Observem que, de certa forma, o Segredo 12 lembra o Segredo 9, não lembra?)
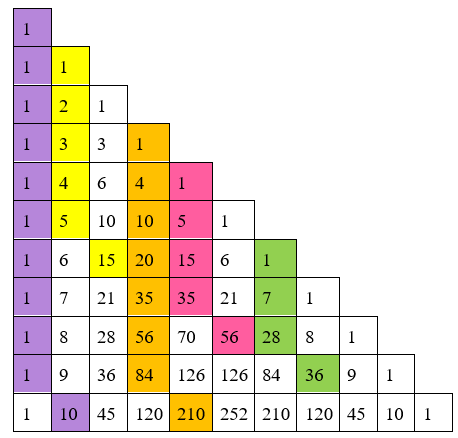
Se tentarmos levar a propriedade anterior para um Triângulo de Pascal na forma de triângulo retângulo, substituindo diagonais por colunas, obtemos a propriedade conhecida como Teorema das Colunas.
Segredo 13: Se somarmos os [tex]k[/tex] primeiros elementos de qualquer coluna de um Triângulo de Pascal na forma de triângulo retângulo, obtemos o número que se encontra abaixo do último elemento, mas à direita.
Visualizem alguns exemplos!
Equipe COM – OBMEP
