Alguns segredos
Essas propriedades são úteis em alguns cálculos matemáticos, tanto que algumas são utilizadas desde a antiguidade. O matemático chinês Jia Xian, por exemplo, utilizou essa famosa representação triangular para estudar as expressões binomiais no século XI.
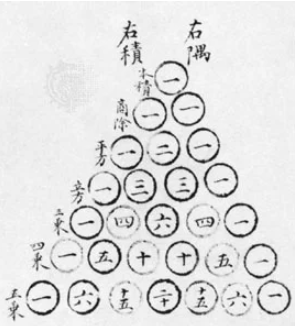 Imagem extraída da Enciclopédia Britânica
Imagem extraída da Enciclopédia Britânica
Vários padrões foram recentemente descobertos, como por exemplo o desenho do Triângulo de Sierpinski.
Assim, o objetivo desta sala é apresentar de forma prática e intuitiva algumas propriedades (nossos segredos) do Triângulo de Pascal, pela mera observação do triângulo.
Vamos lá??
Vamos iniciar com a Propriedade 1, já apresentada na Sala inicial.
Segredo 1: O Triângulo de Pascal na sua representação como um triângulo isósceles é simétrico com relação a uma linha vertical imaginária que passa pelo meio da representação.
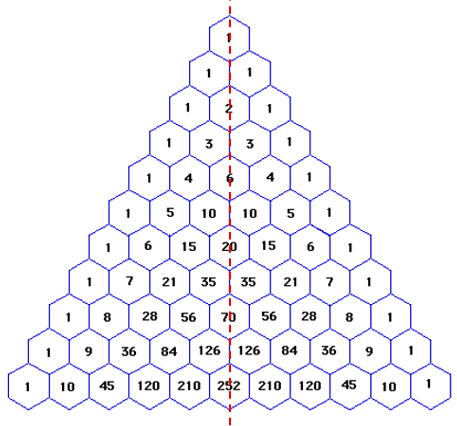
Assim, numericamente falando, os termos (ou as entradas) que estão equidistantes da extremidade mais próxima na representação do Triângulo de Pascal como um triângulo isósceles possuem o mesmo valor.
Em função dos próximos quatro segredos, colorimos algumas células das duas representações do Triângulo de Pascal.
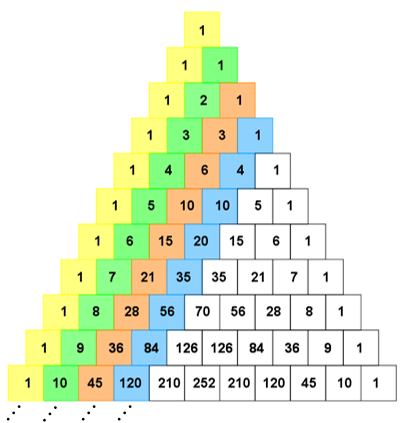
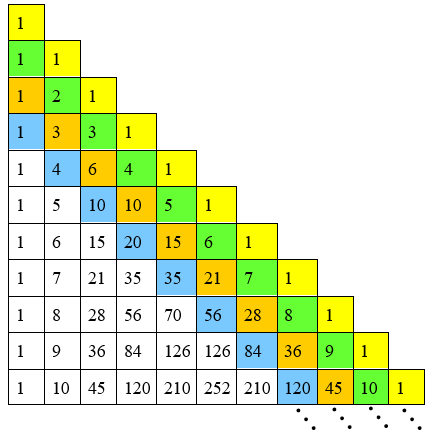
Qual o segredo que cada uma dessas diagonais coloridas esconde?
Se precisarem de ajuda, cliquem no botão abaixo.
Potências de 2 e potências de 11 aparecem com regularidade no Triângulo de Pascal!
Como encontrá-las?
Cliquem no botão abaixo.
A Sequência de Fibonacci é mais uma sequência presente no Triângulo de Pascal.
Não conhecem essa sequência numérica?
Não conseguiram encontrá-la?
Então, é só clicar no botão abaixo!
E se, a partir da representação do Triângulo de Pascal como um triângulo retângulo, somarmos todas as k primeiras entradas de uma diagonal qualquer. O que obteremos?
Vejam a resposta, clicando no botão abaixo!
Já que os últimos segredos envolveram somas, vamos continuar somando…
O que acontecerá se somarmos todos as entradas do Triângulo de Pascal da Linha zero até qualquer outra linha?
Pensem um pouquinho, façam as contas e cliquem no botão abaixo para conferir.
As propriedades contidas nos próximos segredos são bem simples de serem visualizadas.
Cliquem no próximo botão para conhecê-las.
Que tal uma brincadeira?
Consideremos uma malha quadriculada 4 × 4, como a da figura abaixo, na qual está fixado o vértice A.
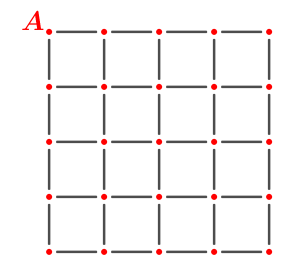
Qual a quantidade de “caminhos mais curtos” que existem entre o ponto A e qualquer um dos 24 outros pontos vermelhos da malha, caminhando sobre os lados dos quadradinhos e se movendo apenas “da esquerda para a direita” ou “de cima para baixo” (sem voltar)?
Cliquem no próximo botão para visualizarem alguns exemplos e conferirem suas respostas.
Todos nós já nos enroscamos algumas vezes na hora de simplificar expressões algébricas, não é?
Portanto, conhecemos a utilidade dos chamados produtos notáveis, já que eles são constantemente utilizados em simplificações.
Algumas dessas ferramentas matemáticas têm relação com o Triângulo de Pascal?
Pensem um pouquinho e, se precisarem de ajuda, cliquem no botão abaixo.
Vocês sabem o que são fractais?
Já ouviram falar do Triângulo de Sierpinski?
Sabendo ou não, já deu para perceber que esses conceitos estão ligados ao próximo segredo, não é?
Então, estão esperando o quê?
Cliquem no botão abaixo!
O próximo segredo que vamos compartilhar é fundamental para tratarmos rigorosamente as propriedades que deram origem aos segredos apresentados nesta Sala; e, conforme já informamos, as demonstrações dessas propriedades farão parte de uma Sala de Estudo sobre o Triângulo de Pascal que abriremos brevemente.
Cliquem no próximo botão para terem acesso à propriedade contida nesse segredo e que pode ser visualizada com o gif animado abaixo.
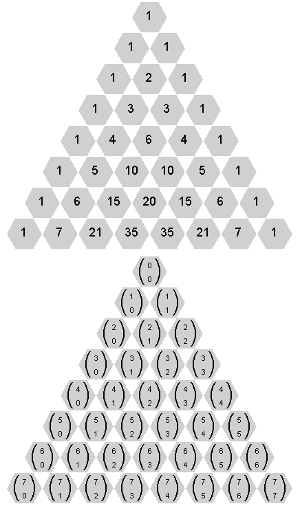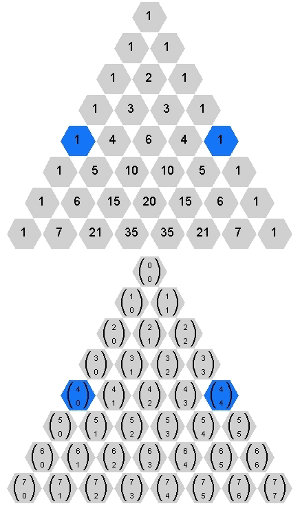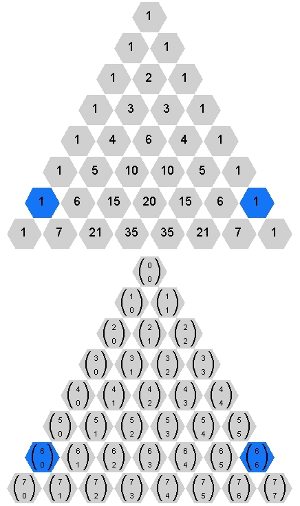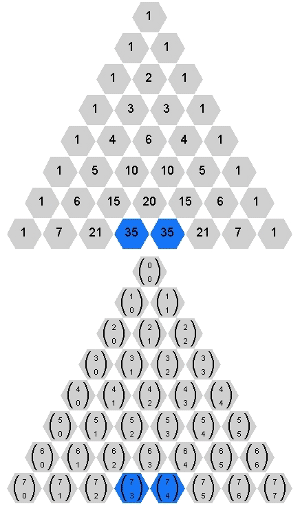
Antes de encerrarmos as nossas “fofocas”, uma breve observação.
Vocês, que já estavam adaptados às discussões sem demonstrações, devem ter estranhado o tratamento mais formal que utilizamos na apresentação do Segredo 17, não é?
– Pois bem, a propriedade contida no Segredo 17 será a primeira a ser discutida na Sala de Estudo sobre o Triângulo de Pascal, uma vez que a equivalência que apresentamos entre as duas maneiras de definirmos esse objeto matemático será fundamental para o desenvolvimento dessa nova Sala.
Feita a observação, vamos ao nosso último ( Último??? ) segredo.
Equipe COM – OBMEP
