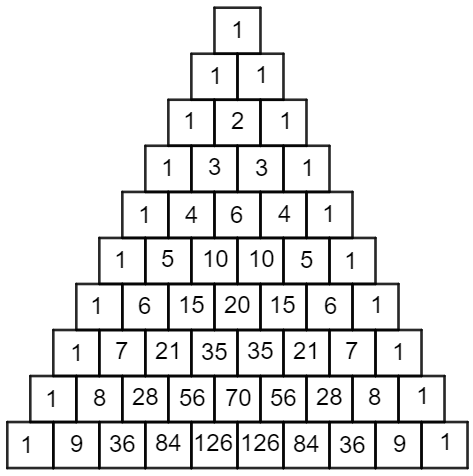
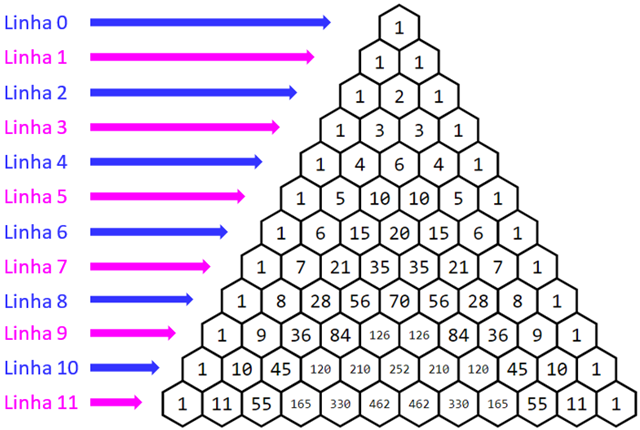
Nesta Sala vamos apresentar uma tabela infinita de números naturais dispostos em posição triangular que se tornou famosa por exibir propriedades aritméticas verdadeiramente surpreendentes: o Triângulo de Pascal.
Apesar de levar o nome de Blaise Pascal (1623-1662), esse triângulo já havia sido estudado na China pelo matemático Yang Hui (1238-1298); mas foi Pascal que sistematizou algumas de suas propriedades.
Yang Hui estudou e popularizou uma representação triangular criada pelo matemático chinês Jia Xian (cerca de 1010-1070), motivo pelo qual na China o Triângulo de Pascal é chamado de Triângulo Yanghui.
O Triângulo de Pascal é também conhecido como Triângulo de Tartaglia, pseudônimo do matemático italiano Niccolò Fontana (1500-1557) ou, simplesmente, como Triângulo Numérico.
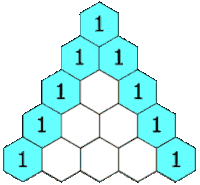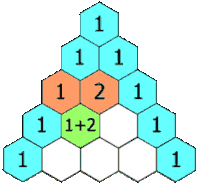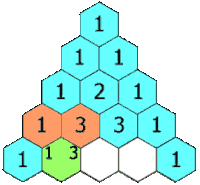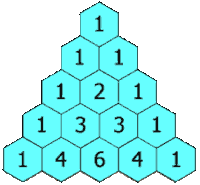Imagem extraída da Wikipédia
Mas afinal, que triângulo é esse?
O Triângulo de Pascal é um triângulo numérico infinito no qual são dispostos, em linhas, números naturais obtidos recursivamente. Os números são obtidos de maneira única e são organizados sequencialmente na forma de um triângulo isósceles, ou de um triângulo retângulo, de modo que:
(1) A primeira linha tem apenas o número 1.
(2) Cada linha seguinte tem um elemento a mais do que a anterior.
(3) A partir da segunda linha, cada linha começa e termina por 1.
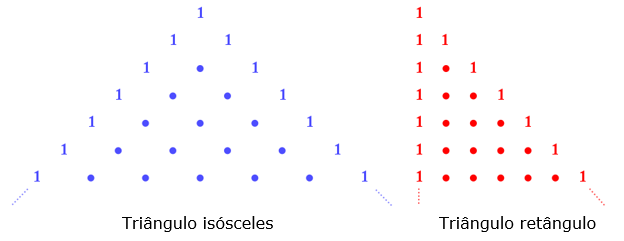
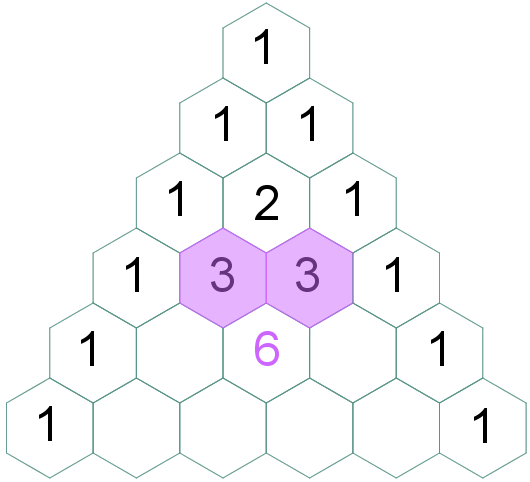
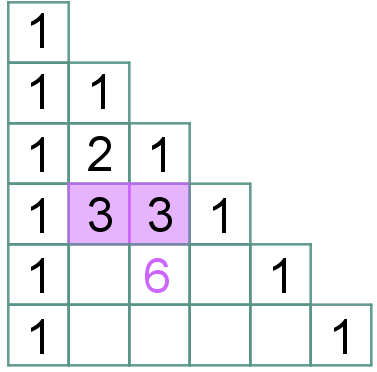
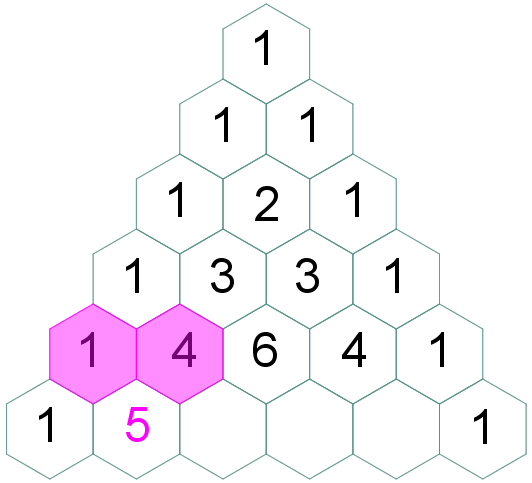
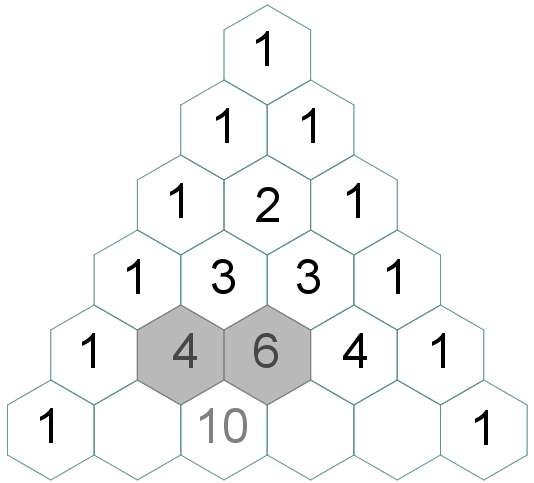
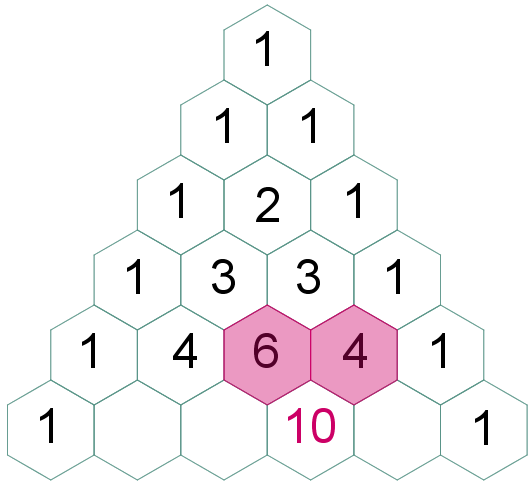
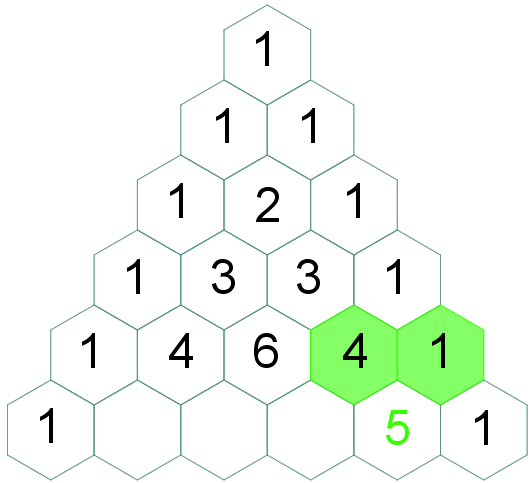
(4.1) No triângulo isósceles, a partir da terceira linha, cada elemento central será a soma dos dois números que são adjacentes a ele (à direita e à esquerda) na linha anterior. |
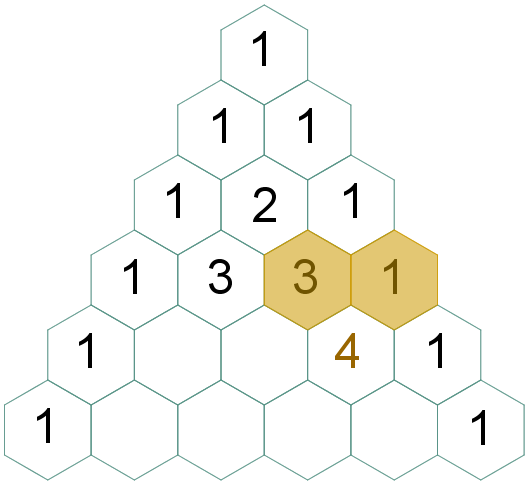
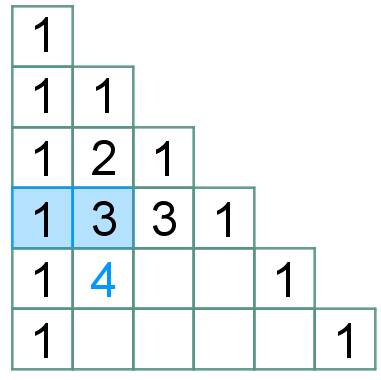
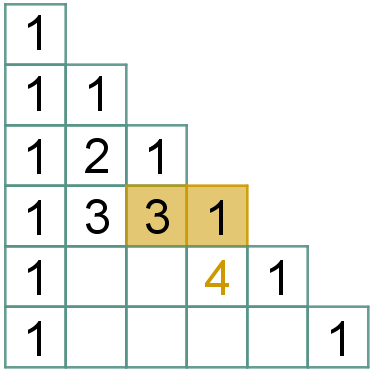
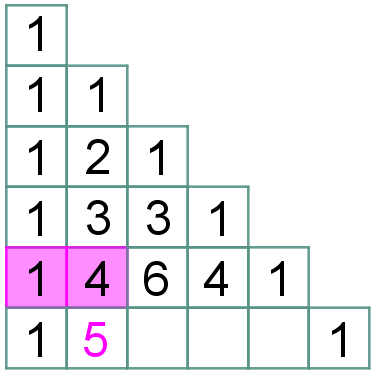
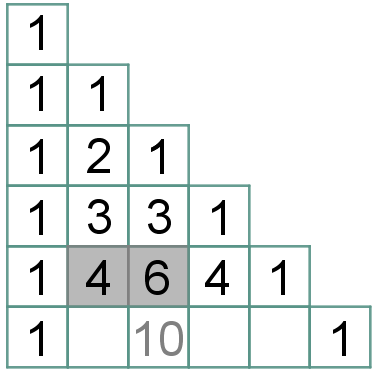
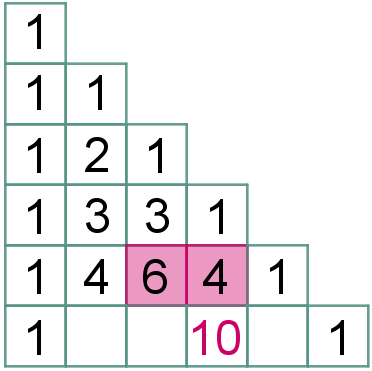
(4.2) No triângulo retângulo, a partir da terceira linha, cada elemento central será a soma dos dois números que estão acima e à esquerda dele na linha anterior.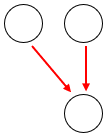
|
Observação: Lembrem-se de que, teoricamente, o Triângulo de Pascal tem infinitas linhas. Mas, quando fazemos uma “representação com as n primeiras linhas do Triângulo de Pascal”, é comum dizermos que representamos um Triângulo de Pascal de n linhas.
Vamos, por exemplo, construir um Triângulo de Pascal com seis linhas.
Pelas regras (1) e (2) segue que:
|
 
|
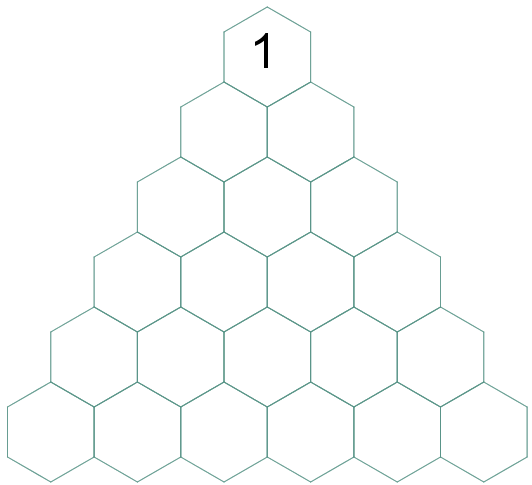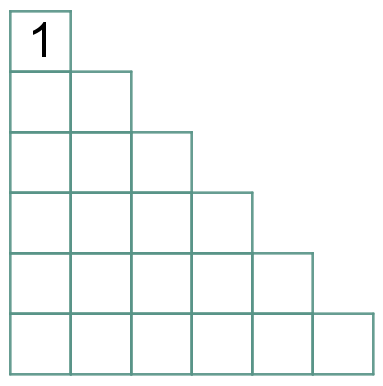
Agora, vamos utilizar a regra (3):
|
  |
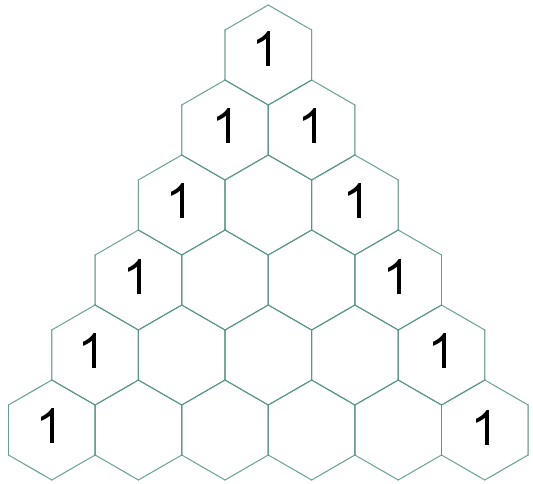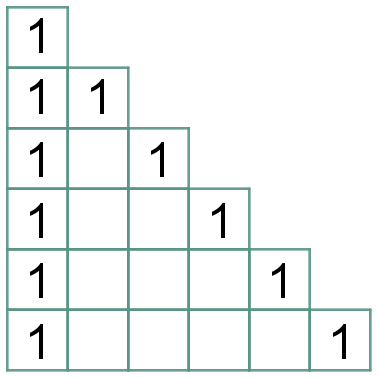| Para finalizar, vamos definir os elementos centrais de cada linha. Pela regra (4) segue que:
|
  
|
   |
|
   |
   |
|
   
|
    |
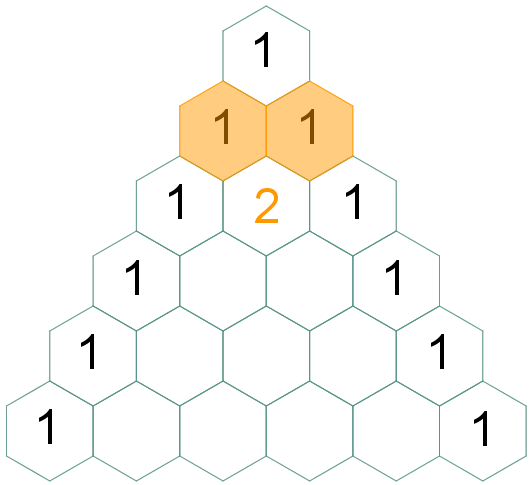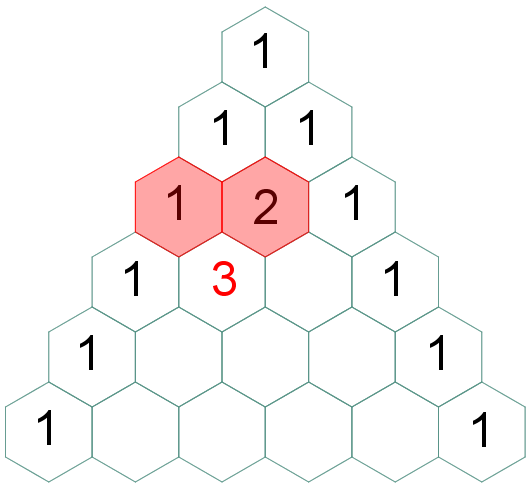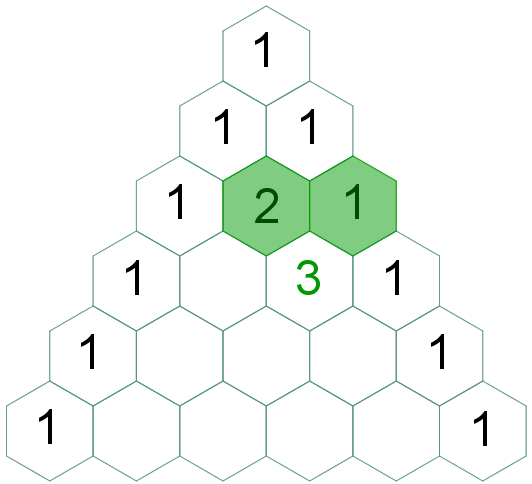
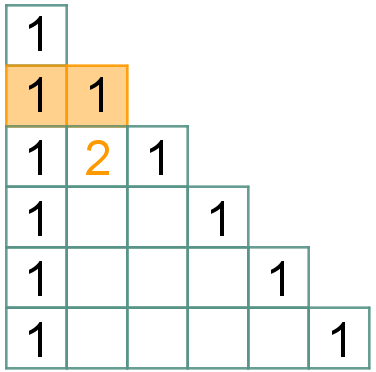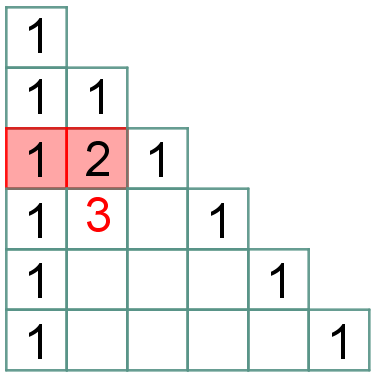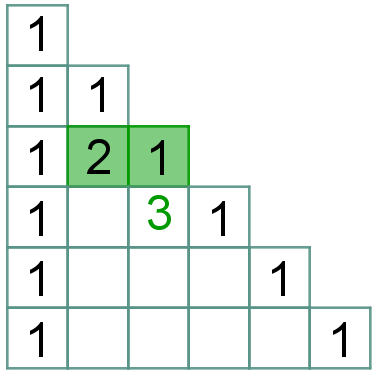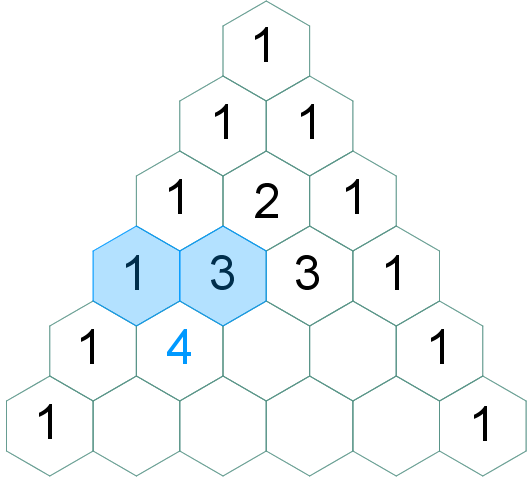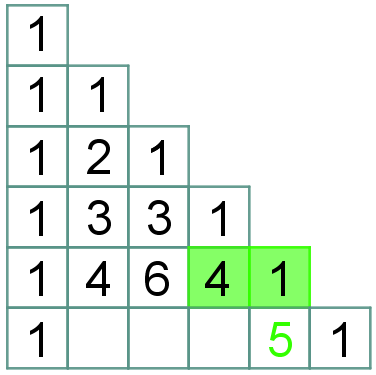Pelo exposto, o Triângulo de Pascal com seis linhas fica assim definido:
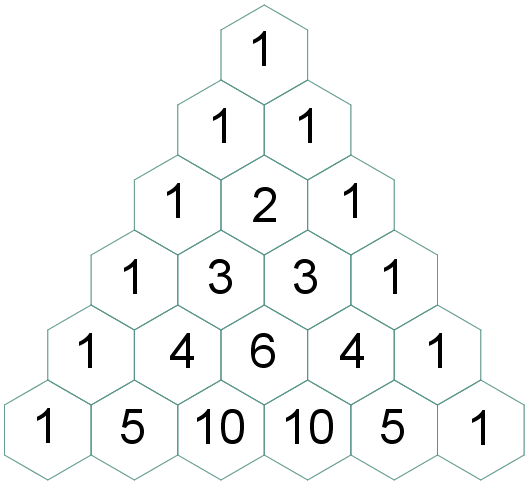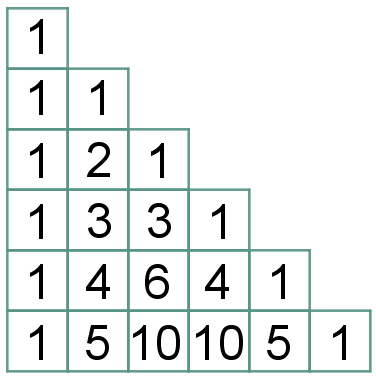ou 
ou 
Com as formas do lado esquerdo, as respectivas construções dos triângulos ficam mais fácil de serem visualizadas; mas, na resolução de problemas, as formas do lado direito são mais utilizadas.
É comum denominarmos a primeira linha do Triangulo de Pascal de Linha 0; a segunda linha de Linha 1; a terceira, de Linha 2 e assim sucessivamente. (Lembrem-se de que, teoricamente, o Triângulo de Pascal tem infinitas linhas!)
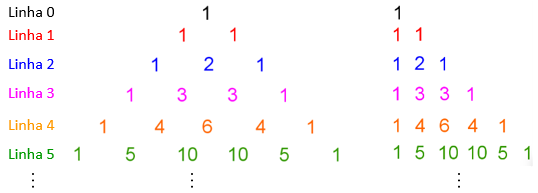
Agora, que tal vocês tentarem construir alguns Triângulos de Pascal?
 |
Nesta página, vocês conseguem gerar até a Linha 30 de um Triângulo de Pascal. |
Propriedades do Triângulo de Pascal
Devido à forma como os números estão dispostos no Triângulo de Pascal, é possível encontrar várias propriedades definidas por eles. Particularmente, esse triângulo numérico infinito tem aplicações na área de Análise Combinatória e Probabilidade, facilitando cálculos graças às suas propriedades. Na continuação desta Sala, vamos apresentar algumas curiosidades e propriedades matemáticas, utilizando representações finitas convenientes do Triângulo de Pascal para ilustrá-las.
Algumas das curiosidades e propriedades do Triângulo de Pascal envolvem números que estão em suas linhas; outras, envolvem números das colunas. O que denominaremos de linhas do Triângulo de Pascal já foi anteriormente definido; resta-nos especificar o que denominaremos por colunas.
Diferentemente das linhas, colunas correspondentes do Triângulo de Pascal podem gerar sequências de números distintos, dependendo da representação que estivermos trabalhando: na forma de um triângulo isósceles ou na forma de um triângulo retângulo. Na figura abaixo, vemos, por exemplo, que os números que aparecem na primeira, na segunda e na terceira colunas da imagem à esquerda não são os que aparecem na primeira, na segunda e na terceira colunas da imagem à direita, respectivamente. Além disso, a ideia de coluna se mostra um pouco estranha quando utilizamos a representação do Triângulo de Pascal na forma de um triângulo isósceles!
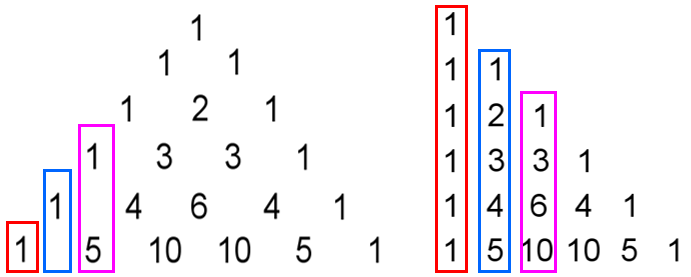
Dessa forma, nos referiremos a colunas do Triângulo de Pascal somente se este estiver representado na forma de um triângulo retângulo. Neste caso, denominaremos as colunas, da esquerda para a direita, como Coluna 0, Coluna 1, Coluna 2, Coluna 3 e assim sucessivamente. (Observe que, teoricamente, a representação do Triângulo de Pascal na forma de triângulo retângulo tem infinitas colunas!)
Por outro lado, a ideia geométrica de diagonal aparece naturalmente na representação do Triângulo de Pascal na forma de um triângulo isósceles, da esquerda para a direita e da direita para a esquerda, e também na forma de um triângulo retângulo, da direita para a esquerda.
E mais, as entradas numéricas definidas sequencialmente pelas diagonais da esquerda para a direita na representação do Triângulo de Pascal na forma de um triângulo isósceles são as mesmas definidas, na mesma sequência, pelas diagonais da direita para a esquerda, tanto na representação na forma de um triângulo isósceles como na representação na forma de um triângulo retângulo.
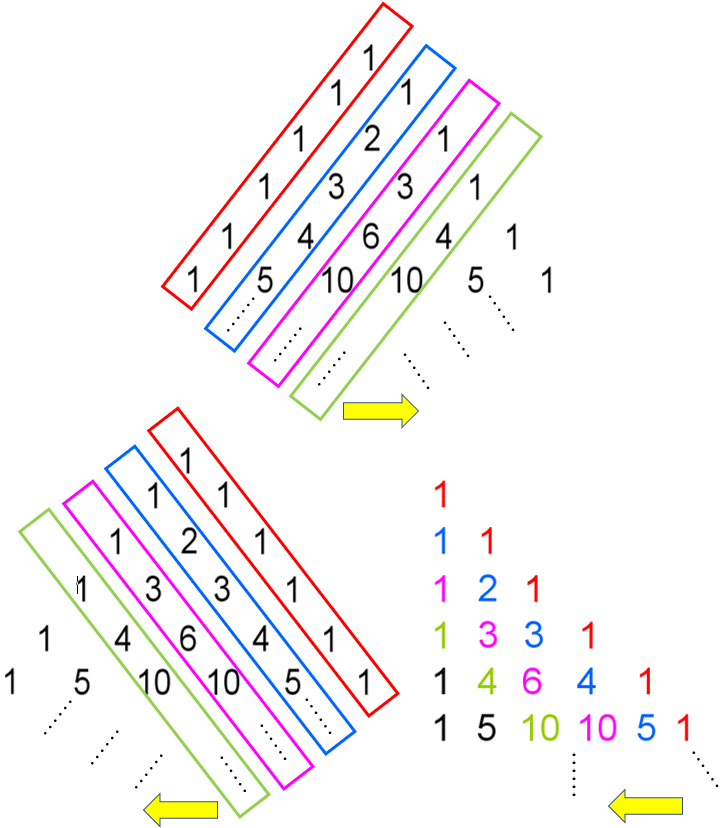
Observem que representação do Triângulo de Pascal na forma de um triângulo isósceles as sequências numéricas definidas pela primeira diagonal, pela segunda diagonal, pela terceira diagonal, e assim sucessivamente, da esquerda para a direita são iguais respectivamente às sequências numéricas definidas pela primeira diagonal, pela segunda diagonal, pela terceira diagonal, e assim sucessivamente, da direita para a esquerda. Assim, temos uma característica importante dessa representação: a simetria do Triângulo de Pascal na forma de um triângulo isósceles, com relação a uma linha vertical imaginária que passa pelo meio da representação.
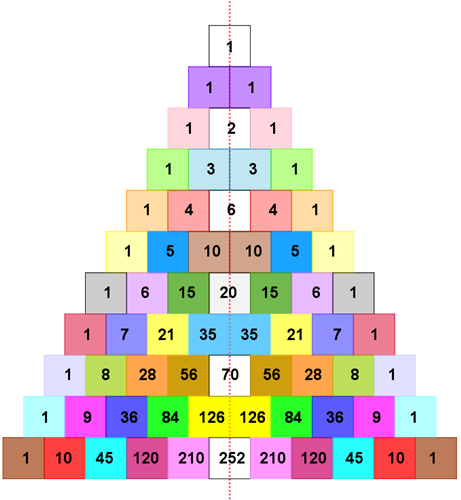
Esta será, então, a primeira dentre as diversas propriedades que iremos apresentar, justificar e ilustrar.
Propriedade 1: O Triângulo de Pascal na sua representação como um triângulo isósceles é simétrico com relação a uma linha vertical imaginária que passa pelo meio da representação.
Vocês estranharam que não mencionamos “demonstrar” quando nos referimos às propriedades que serão apresentadas?
Pois é, como esta é uma Sala para Leitura, não demonstraremos as propriedades com as quais trataremos. No entanto, todas elas serão rigorosamente demonstradas em uma Sala de Estudo que abriremos brevemente.
Vejam quantos segredos estão escondidos nas linhas, colunas e diagonais do Triângulo de Pascal, clicando no botão abaixo.
Equipe COM – OBMEP
Maio de 2023.
Referências
[01] Análise Combinatória e Probabilidade – Augusto César Morgado; João Bosco Pitombeira de Carvalho; Paulo Cesar Pinto Carvalho e Pedro Fernandez.
[02] História da Matemática – Carl B. Boyer, tradução de Elza F. Gomide.
[03] Cuaderno de Cultura Científica (Último acesso em 03/05/23)
[04] O misterioso e enigmático mundo de Pascal e Fibonacci (Último acesso em 03/05/23)
[05] O Triângulo de Pascal (Último acesso em 03/05/23)
[06] O Triângulo de Pascal (UFF) (Último acesso em 03/05/23)
[07] O triângulo de Pascal é de Pascal? (Último acesso em 03/05/23)
[08] Patrones en el triángulo de Pascal (Último acesso em 03/05/23)
[09] Portal da Matemática – Soma de Elementos em Linhas, Colunas e Diagonais (Último acesso em 03/05/23)
[10] Sucesión de Fibonacci (Último acesso em 03/05/23)
[11] UMA EXTENSÃO PARA O COEFICIENTE BINOMIAL: O Coeficiente Trinomial (Último acesso em 03/05/23)
[12] WIKILIVROS – Matemática divertida/Triângulo de Pascal (Último acesso em 03/05/23)
[13] Wikipédia – Blaise Pascal (Último acesso em 03/05/23)
[14] Wikipédia – Sequência de Fibonacci (Último acesso em 03/05/23)