✏ Link da Sala para dispositivos da Apple.
Ao Infinito e Além!
Esperamos, desse modo, que a leitura deste material facilite a compreensão de algumas dessas ideias tão intrigantes (e inicialmente absurdas) que, inclusive, demoraram muito tempo a serem desenvolvidas com o rigor matemático que hoje conhecemos.
Apertem os cintos e
BOA VIAGEM!
 GIF extraído de Tenor Imagens (Acesso em 23/11/23)
GIF extraído de Tenor Imagens (Acesso em 23/11/23)
Mas o que é o infinito?
De acordo com o dicionário Michaelis On-line, infinito é:
2. [Matemática] Grandeza que não se consegue calcular, medir.”
No entanto, essas definições parecem se perder dentre as áreas da Filosofia, da Religião, das Artes… e da Matemática também.
Pode um infinito estar contido em um espaço delimitado?
E pode um infinito caber em outro, como se estivesse “dentro” dele, sendo que os dois, pela própria noção intuitiva de infinito, não teriam fim?
Onde a Matemática entra nessa conversa?
I – Um Pouco de Contexto…
Antes de entrarmos na densa teoria de infinitos, vamos pensar: como o infinito se caracteriza no senso comum?
Desde o nosso contato inicial com os números, na mais tenra infância, nos deparamos com a possibilidade de sempre existir um número após o 1, outro após o 2, após o 3…; qual é, então, o último número?
Essa questão intriga pequenos grandes matemáticos de todo o mundo, o que os leva a questionar os adultos:
– Onde terminam os números?
e a resposta é, geralmente, a mesma seca e vazia frase:
– Eles não terminam.
Com o tempo, essa é uma ideia que vai amadurecendo e, ao longo da juventude, novos problemas (e dilemas filosóficos) envolvendo o infinito começam a surgir:
– Será que o espaço é infinito?
– E o tempo?
– Será que ficaremos juntos para sempre?
Sem falar no que passa na nossa cabeça antes de uma prova de matemática:
– O que significa um conjunto ser infinito?
– Todos os conjuntos infinitos têm a mesma quantidade de elementos?
– Há um infinito entre o 0 e o 1? Mas e aquele entre o 0 e o 2? É maior do que o primeiro?
Essas questões são muito recorrentes em nossas vidas (e, por vezes, mal compreendidas), de modo que acabam se refletindo também em nossa cultura. Talvez você se recorde, por exemplo, de como o infinito foi tratado na adaptação para o cinema do livro A Culpa é das Estrelas, de John Green, no momento em que Hazel faz um elogio a Gus.
Confira, é só clicar na setinha!
Apesar de ser um belo discurso, matematicamente falando, ele está incorreto.
Pois é… sinto muito, Hazel, mas você estava errada. Não; o infinito entre 0 e 2 não é maior do que o infinito entre 0 e 1!
Mas isso explicaremos mais tarde.
II – Um pouco de Matemática
Vamos analisar primeiramente o que entendemos por um conjunto com um número finito de elementos. Para este propósito será necessário o importante conceito de função bijetora. Se você não se lembra dele, clique no botão abaixo;
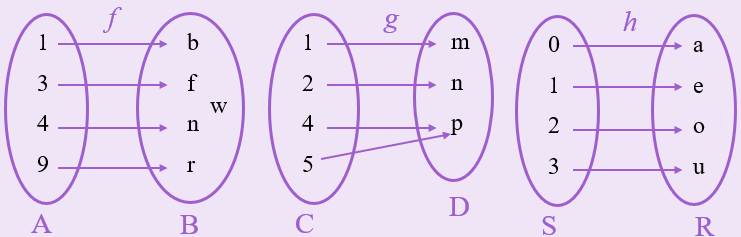
Vejamos, de forma mais detalhada, como funciona o processo de atribuir a um conjunto finito, digamos A=[tex]\{\diamondsuit, \triangledown, \square, \heartsuit, \circ\}[/tex], o seu número de elementos.
Dizemos que esse conjunto A possui 5 elementos devido ao fato de existir uma função bijetora entre ele e o conjunto {1, 2, 3, 4, 5}, como por exemplo:
[tex] \qquad \qquad \begin{array}{ccc}
1 & \longleftrightarrow & \diamondsuit \\
2 & \longleftrightarrow & \triangledown \\
3 & \longleftrightarrow & \square \\
4 & \longleftrightarrow & \heartsuit \\
5 & \longleftrightarrow & \circ \\
\end{array}[/tex]
Definição: De um modo geral, um conjunto A diz-se finito, ou que possui uma quantidade finita de elementos, quando existe, para algum [tex]n\in \mathbb{N}[/tex], uma função bijetora do conjunto [tex]\{1, 2, \dots, n\}[/tex] no conjunto A. Neste caso, dizemos que A possui n elementos ou que a cardinalidade de A é n. É usual utilizar a notação #A = n (ou n(A)=n).
Por outro lado, dizemos que um conjunto A é infinito, ou que possui infinitos elementos, quando ele não é finito, ou seja, para qualquer [tex]n\in \mathbb{N}[/tex], não existe uma função bijetora do conjunto [tex]\{1, 2, \dots, n\}[/tex] no conjunto A.
Alguns fatos sobre conjuntos finitos são muito úteis para se entender os conjuntos infinitos. Vejamos dois deles.
➤ Observe que, de acordo com exposto acima, dois conjuntos finitos A e B possuem o mesmo número de elementos ou a mesma cardinalidade (#A = #B) quando existe uma função bijetora entre eles.
- ● Vejamos um exemplo ilustrativo desse fato. Consideremos os conjuntos A=[tex]\{\diamondsuit, \triangledown, \square\}[/tex] e B=[tex]\{ \heartsuit, \circ, \triangle\}.[/tex] Como cada um destes conjuntos possui 3 elementos, existem funções bijetoras [tex]\sigma: \{1, 2, 3\} \to [/tex] A e [tex]~\tau : \{1, 2, 3\} \to[/tex] B, como por exemplo:
[tex]\qquad \begin{array}{ccc}
& \sigma & \\
1 & \longleftrightarrow & \diamondsuit \\
2 & \longleftrightarrow & \triangledown \\
3 & \longleftrightarrow & \square \\
\end{array} \ \ \ \ \ \begin{array}{ccc}
&\tau & \\
1 & \longleftrightarrow & \heartsuit \\
2 & \longleftrightarrow & \circ \\
3 & \longleftrightarrow & \triangle\\
\end{array}[/tex]
Podemos usar essas duas funções para construir uma função bijetora entre A e B:
[tex]\qquad \begin{array}{ccc}
\diamondsuit & \longleftrightarrow & \heartsuit \\
\triangledown & \longleftrightarrow & \circ \\
\square & \longleftrightarrow & \triangle\\
\end{array}[/tex]
➤ Outro fato muito importante é que um conjunto finito A possui um número menor de elementos do que um conjunto finito B, ou a cardinalidade de A é menor do que a cardinalidade de B, quando existe uma função bijetora de A com um subconjunto de B, mas não existe função bijetora entre A e B.
-
● Novamente consideremos um exemplo ilustrativo com os conjuntos A=[tex]\{ \diamondsuit, \triangledown \}[/tex] e B=[tex]\{ \square, \heartsuit, \circ, \triangle\}.[/tex]
Podemos exibir a função bijetora entre A e o subconjunto [tex]\{ \square, \heartsuit\}[/tex] de B
[tex]\qquad \begin{array}{ccc}
\diamondsuit & \longleftrightarrow & \heartsuit \\
\triangledown & \longleftrightarrow & \square \\
\end{array}[/tex]
mas o leitor não terá trabalho em se convencer de que jamais poderemos exibir uma função bijetora entre A e B. Dessa forma, dizemos que a cardinalidade de A é menor do que a cardinalidade de B.
Podemos fazer analogias com estes fatos sobre os conjuntos finitos no caso de conjuntos infinitos.
➤ Dizemos que dois conjuntos infinitos A e B possuem a mesma cardinalidade, ou mesma extensão, quando existe uma função bijetora entre A e B. Neste caso, também utilizamos a notação #A = #B.
➤ Dizemos também que o conjunto infinito A possui cardinalidade inferior à cardinalidade do conjunto infinito B, ou ainda que a extensão de A é menor do que a extensão de B, quando existe uma função bijetora de A com um subconjunto de B, mas não existe função bijetora entre A e B.
Observe que, nos casos em que um conjunto é finito, utilizamos o seu número de elementos para indicar a sua cardinalidade, ou seja, o seu “tamanho”. Agora, para se indicar a cardinalidade de um conjunto infinito, ou o seu “tamanho”, foram criados os chamados números transfinitos. Um deles será apresentado no item IV.
Na próxima seção veremos como essas ideias foram historicamente introduzidas na Matemática.
III – Um Pouco de História…
Zenão de Eleia (490 – 430 a.C.) era discípulo do conhecido filósofo Parmênides, o qual defendia fortemente que a mudança é impossível e a pluralidade (ideia de que as coisas possuem diversos estados, ao invés de um só) não existe. Buscando defender as ideias de seu mestre, Zenão possuía a estratégia de supor teses que queria atacar (por exemplo, a infinidade de pontos em uma reta), deduzir uma consequência que levasse à contradição, chegando, por fim, a uma redução ao absurdo. Iremos entender esse processo agora, com um de seus paradoxos mais famosos:
O Paradoxo da Flecha
Um arqueiro lança uma flecha que adquire movimento. Para que a flecha alcance o alvo, ela deve primeiro percorrer metade da distância entre si mesma e o alvo. No entanto, antes de percorrer essa metade, ela deve percorrer um quarto da distância, e antes disso, um oitavo, e assim por diante.
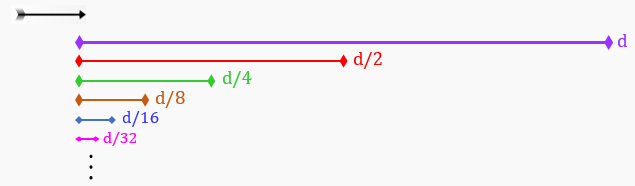 Essa divisão continua infinitamente, resultando em uma quantidade infinita de etapas a serem concluídas antes que a flecha possa, de fato, atingir o alvo.
Essa divisão continua infinitamente, resultando em uma quantidade infinita de etapas a serem concluídas antes que a flecha possa, de fato, atingir o alvo.
A implicação aparente desse paradoxo é que, dado o número infinito de etapas necessárias para que a flecha alcance o alvo, ela nunca realmente atingirá o alvo, já que as infinitas etapas não podem ser concluídas. Isso desafia a nossa intuição sobre o movimento e a divisibilidade do espaço.
 Imagens extraídas de FisikanaRede e Canva Imagens. (Acesso em 23/11/23)
Imagens extraídas de FisikanaRede e Canva Imagens. (Acesso em 23/11/23)
Ao descrever essa contradição, tendo como principal objetivo defender uma tese filosófica, Zenão de Eleia acabou por, sem querer, iniciar a discussão matemática formal acerca da existência de infinitos, começando a partir de segmentos que podem ser divididos em partes infinitamente pequenas por meio de divisões sucessivas.
Essa discussão avançou no período da Idade Clássica, com as noções de Aristóteles (384 – 322 a.C.) acerca do infinito, as quais buscam, sobretudo, expor as contradições do Paradoxo da Flecha de Zenão.
Aristóteles, por meio de sua tese sobre ato e potência, afirma existir um infinito potencial e um infinito atual.
O infinito potencial ocorre como um processo sem fim ao longo do tempo em objetos que, entretanto, são factualmente finitos. Assim, um infinito potencial é um processo sem fim ao longo do tempo, mas que é finito em qualquer momento específico. O infinito atual, ou real, existe em ato e de todo a um dado momento; logo, seria uma infinidade total e completa.
Portanto, com o infinito potencial tem-se a possibilidade de ir sempre mais longe (inesgotável) e com infinito atual tem-se uma infinidade realizada (esgotada). O caso do infinito potencial aplica-se, por exemplo, às divisões infinitas de um objeto finito, enquanto o infinito atual diz respeito, por exemplo, a conjuntos infinitos, ou seja, infinitos em ato.
Discussões sobre o infinito, no entanto, mantiveram-se estagnadas durante muitos séculos, e os paradoxos de Zenão não foram de todo esclarecidos. Os matemáticos somente ousaram levantar novamente essa questão no século XV, durante o Renascimento. Duas importantes figuras se destacaram: Giordano Bruno, o qual, com sua obra Acerca do Infinito, do Universo e dos Mundos, argumentou que o Universo era infinito e que continha um número infinito de mundos; e Galileu Galilei, que dissertou sobre a equicardinalidade do conjunto dos inteiros e dos quadrados perfeitos.
Foi no desenvolvimento do Cálculo, por Gottfried Leibniz e Isaac Newton, com os estudos sobre sequências e séries convergentes e o estabelecimento do conceito de limite, que paradoxos como os de Zenão adquiriram uma outra interpretação. Expressões infinitesimais como a soma das potências de ½ adquiriram novo sentido.
Uma Soma dos Infinitos Termos
[tex]1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots=2[/tex]
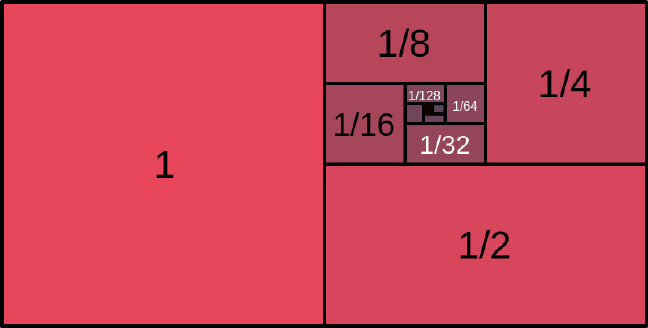 Imagem extraída de Wikipédia. (Acesso em 23/11/23)
Imagem extraída de Wikipédia. (Acesso em 23/11/23)
No entanto, foi só no século XIX que os “tamanhos” dos infinitos passaram a ser cautelosamente analisados e estudados, principalmente com a aparição de uma importante figura: Georg Cantor (1845 – 1918).
Não é exagero dizer que Cantor foi o matemático que mais contribuiu para a definição do infinito e delimitação do estudo desse conceito, por meio de seu trabalho no âmbito de teoria dos conjuntos: suas ideias permitiram a sistematização do estudo do infinito, a partir da elaboração de uma teoria hoje entendida e reconhecida como um dos pilares da Matemática.
Georg Ferdinand Ludwig Philipp Cantor
Georg Cantor foi o principal expoente no estudo dos infinitos.
 Imagem extraída de BBVA Openmind. (Acesso em 23/11/23)
Imagem extraída de BBVA Openmind. (Acesso em 23/11/23)
A partir da definição de número transfinito, Cantor demonstrou que nem todos os infinitos são iguais, desenvolvendo a noção de que existem infinitos de “diferentes tamanhos”, tamanhos esses conhecidos como cardinalidades (ou potências ou extensões). De fato, Cantor demonstrou que “existem mais números reais do que números naturais“, apesar de ambos serem infinitos. Explicaremos essas ideias e a tese de Cantor mais detalhadamente no item IV.
Um dos principais colaboradores e defensores das ideias de Georg Cantor foi David Hilbert (1862 – 1943), o qual descreveu como paraíso o trabalho sobre infinitos desenvolvido por Cantor. Bastante conhecido por propor no Congresso Internacional de Matemáticos de Paris, em 1900, os 23 Problemas que muito influenciaram a Matemática do século XX, Hilbert também foi o idealizador do famoso paradoxo do Hotel de Hilbert.
O Paradoxo do Hotel de Hilbert
O “Hotel de Hilbert” ou “Hotel Infinito”, como também é conhecido, é um conceito paradoxal introduzido por David Hilbert para ilustrar as intrigantes propriedades dos infinitos. Esse paradoxo esclarece os conceitos contraintuitivos propostos por Georg Cantor ao estudarmos os infinitos na Matemática, destacando a ideia de correspondência bijetiva.
- ● Imagine um hotel com infinitos quartos. Agora, imagine que todos eles estão ocupados, ou seja, há um hóspede em cada quarto. Em um dado momento, chega um turista no hotel sem ter feito reserva anteriormente e solicita um quarto. O recepcionista, sem saber como proceder, pois todos os quartos estavam ocupados, chama o gerente para resolver a situação. O gerente, por conseguinte, solicita que o hóspede do quarto 1 vá para o quarto 2; que o hóspede do quarto 2 vá ao quarto 3 e assim por diante…; fazendo sempre com que o hóspede do quarto n vá para o quarto n+1. Desse modo, o turista pôde se alojar no quarto 1 e todos os infinitos hóspedes continuam hospedados nos infinitos quartos.
Considere, posteriormente, que o responsável por um ônibus com infinitos passageiros deseje hospedar todos eles no Hotel de Hilbert. O gerente, que é novamente chamado, pede que o hóspede do quarto 1 vá ao quarto 2; que o hóspede do quarto 2 vá ao quarto 4; que o hóspede do quarto 3 vá ao quarto 6… e assim por diante; ou seja, que o hóspede de cada quarto n vá para o quarto 2n. Dessa forma, todos os infinitos passageiros do ônibus podem se hospedar nos infinitos quartos ímpares, e os infinitos hóspedes originais continuam hospedados no hotel, ocupando agora os infinitos quartos pares.
Dentre tantos objetos esquecidos nos quartos antigos e esbarrões nos infinitos corredores, essa história contada por David Hilbert busca ilustrar a ideia de Cantor de que um infinito é tão grande quanto outro sempre que há uma correspondência de um para um entre todos os elementos de seus conjuntos.
David Hilbert e seu Hotel Infinito.
 Imagens extraídas de Matemática para Quem? e Wikipédia. (Acesso em 23/11/23)
Imagens extraídas de Matemática para Quem? e Wikipédia. (Acesso em 23/11/23)
Agora que entendemos um pouco sobre como a ideia de infinito se desenvolveu ao longo da história, vamos entender um pouco mais sobre as ideias desenvolvidas por Georg Cantor.
IV – Mas, afinal, como pode um infinito ser maior do que outro?
Veja que o que possibilita abrir infinitas vagas no hotel de Hilbert é o fato de que o conjunto dos números naturais pares tem a mesma cardinalidade do conjunto formado pelos números naturais; e, com isso, os infinitos hóspedes que já estavam no hotel podem ficar hospedados apenas nos quartos com números pares. Mais precisamente, na função f que associa cada número natural ao seu dobro, o conjunto A dos números naturais é o domínio e cada elemento desse domínio está associado a um, e somente um, elemento do contradomínio B, que é o conjunto dos números naturais pares. Além disso, todo número do contradomínio está associado a um elemento do domínio ( número par [tex]2m[/tex] está associado ao número natural [tex]m[/tex]).

Dessa forma, todo número [tex]n \in \mathbb{N}[/tex] tem seu correspondente [tex]2n[/tex] e nenhum número “sobra” em qualquer dos dois conjuntos. Logo, esses conjuntos possuem a mesma extensão, e nenhum deles é maior do que outro.
Este caso pode parecer nada intuitivo, afinal o conjunto P dos números pares é um subconjunto próprio do conjunto dos números naturais.
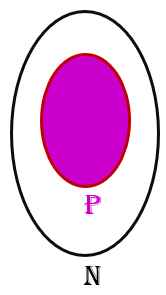 No entanto, quando se trata de conjuntos infinitos, podemos dizer que nem sempre o todo é maior do que a soma de suas partes; e isso ficará mais evidente ainda nos próximos exemplos.
No entanto, quando se trata de conjuntos infinitos, podemos dizer que nem sempre o todo é maior do que a soma de suas partes; e isso ficará mais evidente ainda nos próximos exemplos.
O matemático George Cantor denotou a cardinalidade de conjuntos com a mesma cardinalidade dos números naturais, conhecidos como conjuntos infinitos enumeráveis, pelo número transfinito [tex]\aleph_0[/tex] (alef zero).
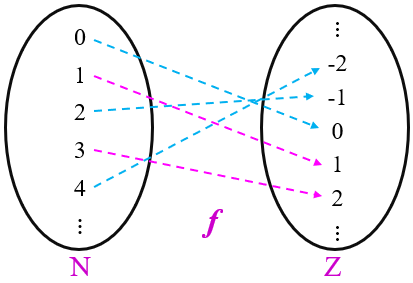
Talvez mais impressionante do que o fato de existir uma bijeção entre [tex]\mathbb{N}[/tex] e seu subconjunto de números pares seja o fato de também existir uma bijeção entre [tex]\mathbb{N}[/tex] e todo o conjunto dos números inteiros [tex]\mathbb{Z}[/tex]; afinal, em [tex]\mathbb{Z}[/tex] estão contidos, além dos naturais, todos os seus simétricos. No entanto, observe a seguinte função [tex] f:\mathbb{N}\rightarrow \mathbb{Z}[/tex] definida por partes:
[tex]f(n)=\begin{cases}
\dfrac{n+1}{2},\text{ se } n \text{ for ímpar} \\
~~\\
– \dfrac{n}{2},\text{ se } n \text{ for par}\\
\end{cases} \, .[/tex]
Você consegue perceber que essa função é bijetora, de tal modo que estabelece uma relação de um para um entre [tex]\mathbb{N}[/tex] e [tex]\mathbb{Z}[/tex]?
Uma característica bastante importante que possuem os números naturais e os números inteiros, e que os diferencia do restante dos números reais, é a existência dos respectivos sucessores, e isso estabelece um ordenamento bastante claro dos elementos dos conjuntos [tex]\mathbb{N}[/tex] e [tex]\mathbb{Z}.[/tex] A cada elemento n de [tex]\mathbb{N}[/tex] ou [tex]\mathbb{Z}[/tex], sabemos que o próximo elemento, chamado de sucessor, é o número n+1 e essa característica não está presente no conjunto [tex]\mathbb{Q}[/tex] dos números racionais. De fato, dado um número [tex]\frac{m}{n} \in \mathbb{Q}[/tex], não sabemos dizer qual é o racional imediatamente maior (ou menor) do que [tex]\frac{m}{n}[/tex] (isso se deve ao fato de o conjunto dos números racionais ser denso… mas vamos deixar essa discussão para outro momento).
Apesar disso, é possível estabelecer uma listagem dos números racionais que possibilite uma contagem desses números, no sentido de associar números naturais a todos os números racionais. Dessa forma, fica estabelecida uma relação bijetora entre os dois conjuntos, e podemos concluir que ambos possuem mesma cardinalidade e são enumeráveis.
A figura abaixo ilustra uma listagem dos números racionais positivos e um procedimento de contagem para eles. A sequência da contagem é indicada pelas flechinhas azuis e um número riscado com um X vermelho significa que ele já apareceu anteriormente em algum momento na contagem.
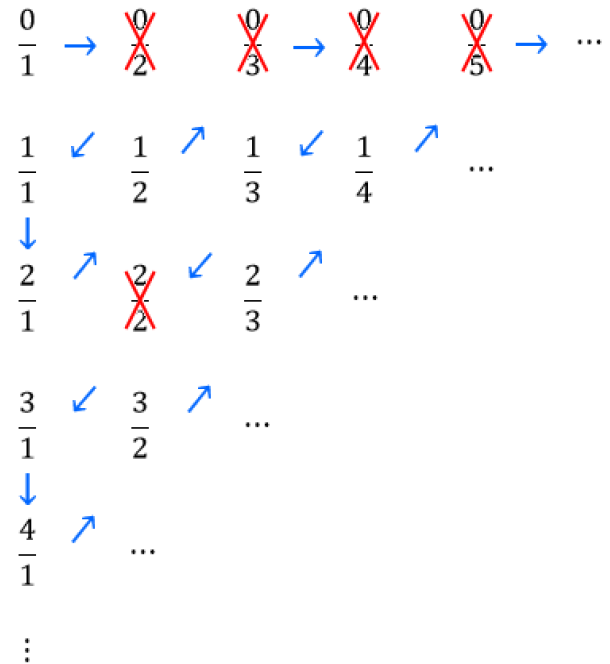
Veja os primeiros termos da sequência na qual ordenamos os racionais positivos:
Até agora, todos os exemplos citados correspondem a conjuntos com mesma cardinalidade. E isso ainda não responde a pergunta:
Existe um conjunto infinito maior do que outro conjunto infinito?
Para responder afirmativamente a essa pergunta, seria suficiente encontrar um conjunto infinito com o qual não consigamos estabelecer uma bijeção com [tex]\mathbb{N}[/tex]. Dessa maneira esse novo conjunto não terá a mesma cardinalidade de [tex]\mathbb{N}[/tex], mas sim uma cardinalidade “maior” ou “menor”. Particularmente, vamos utilizar um conjunto infinito cuja cardinalidade é maior do que a cardinalidade de [tex]\mathbb{N}.[/tex]
Esse conjunto é exatamente o intervalo real [tex]\left(0,1\right)=\{x \in \mathbb{R}\, |\, 0 \lt x \lt 1\}[/tex], aquele mesmo mencionado no filme A Culpa é das Estrelas.
A técnica utilizada para comprovar, inicialmente, que a cardinalidade desse conjunto não é a mesma que a de [tex]\mathbb{N}[/tex] também é devida a Cantor, e é conhecida como diagonalização de Cantor.
Tente imaginar uma relação entre todos os números naturais e todos os números entre 0 e 1. Poderíamos relacionar o 1 com 0,1; o 2 com 0,2; o 3 com 0,3; e assim por diante. Mas é fácil perceber que essa suposta enumeração de números reais entre 0 e 1, apesar de infinita, não cobre todo o intervalo [tex]\left(0,1\right).[/tex] Há uma infinidade de números reais entre 0,1 e 0,2, por exemplo, que não estariam contemplados nessa estratégia.
Imaginemos, então, uma relação mais aleatória. O argumento que vamos utilizar faz uso de uma técnica de demonstração matemática bastante útil: a demonstração por redução ao absurdo. Vamos supor que algo seja verdadeiro e, ao chegar a uma contradição, concluímos que a hipótese inicial era falsa.
Vamos lá!
[tex]\qquad \qquad 1 \text{ com } x_1= 0,a_{11}a_{12}a_{13}\cdots\\
\qquad \qquad 2 \text{ com } x_2= 0,a_{21}a_{22}a_{23}\cdots\\
\qquad \qquad 3 \text{ com } x_3= 0,a_{31}a_{32}a_{33}\cdots\\
\qquad \qquad ~~~~~~~~~~ \vdots\\
\qquad \qquad k \text{ com } x_k= 0,a_{k1}a_{k2}a_{k3}\cdots\\
\qquad \qquad ~~~~~~~~~~ \vdots\\[/tex]
Mas, observe que existe um número especial [tex]D[/tex] que não está contemplado nessa enumeração.
Se definirmos
[tex]\qquad \qquad D=0, d_1d_2d_3\cdots,[/tex]
com os algarismos [tex]d_1\ne a_{11}[/tex]; [tex]d_2\ne a_{22}[/tex]; [tex]d_3\ne a_{33} \cdots[/tex]; [tex]d_k\ne a_{kk}[/tex], e assim por diante, teremos um número que pertence ao intervalo [tex]\left(0,1\right)[/tex] mas que não está enumerado na listagem acima, pois [tex]D[/tex] se diferencia de [tex]x_1[/tex] no primeiro dígito depois da vírgula, de [tex]x_2[/tex] no segundo dígito depois da vírgula, de [tex]x_3[/tex] no terceiro dígito depois da vírgula, etc.
Dessa forma não existe uma bijeção entre o conjunto dos números naturais e o intervalo [tex]\left(0,1\right)[/tex], ou seja, o intervalo [tex]\left(0,1\right)[/tex] não é enumerável.
Por outro lado, observe que existe uma bijeção de [tex]\mathbb{N}[/tex] com o subconjunto [tex]B=\{\frac{1}{2}, \frac{1}{3}, \dots, \frac{1}{n+1}\dots \}[/tex] do intervalo [tex]\left(0,1\right)[/tex] que associa a cada número natural [tex]n[/tex] o número [tex]\dfrac{1}{n+1}[/tex].
Logo, a cardinalidade do conjunto [tex]\left(0,1\right)[/tex] é maior do que a cardinalidade dos números naturais, ou seja, o infinito entre 0 e 1 é maior do que o infinito dos números naturais …
Portanto, SIM: há infinitos maiores do que outros!
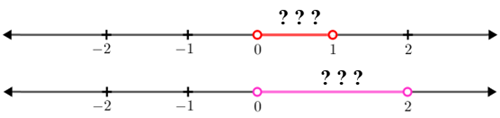
Mas atenção: corrigindo a afirmação de Hazel, o infinito entre 0 e 2 tem o mesmo tamanho do que o infinito entre 0 e 1.
Basta estabelecer a função bijetora [tex]f:\left(0,1\right) \rightarrow \left(0,2\right)[/tex], dada por [tex]f(x)=2x.[/tex]
V – Aplicações interessantes de infinitos
Infinitos são, definitivamente, curiosos. Sabemos que eles existem, no entanto, são inacessíveis à nossa limitada compreensão humana. Algo sem fim desafia completamente qualquer concepção de realidade que nossa mente é capaz de criar, afinal, imaginar números grandes já é uma tarefa difícil…
Se o tamanho de um continente, a distância entre a Terra e o Sol, a proporção entre os componentes de um átomo… já são ideias complexas demais para serem processadas por nosso cérebro, o que dizer, então, sobre algo tão grande que não tem fim?
Quer algo mais perturbador do que saber que no intervalo [tex]\left(0,1\right)[/tex] tem tantos números quanto no intervalo [tex]\left(0,2\right)[/tex]? É só pensar no “tamanho geométrico” dos dois segmentos para ter até calafrios…
Não importa o quanto tente, qualquer tentativa de dimensionar o infinito é falha para a mente humana. E isso pode ser assustador e maravilhoso!
Imagine um macaco de frente para uma máquina de escrever. Por não ser capaz de compreender o significado dos símbolos da máquina, ele aperta as teclas aleatoriamente. Após algum tempo, ele talvez consiga escrever corretamente alguma palavra, ou escrever uma sequência de vogais e consoantes com um padrão de repetição, ou então escrever os números na ordem certa. Quanto mais tempo ele digita, maiores são as possibilidades de padrões. E se esse tempo for infinito, quais padrões ele vai formar?
A resposta é: (quase) todos!
Esse é o Teorema do Macaco Infinito, apresentado por Émile Borel em 1913, e seu objetivo é mostrar como eventos com chances pequenas de ocorrer, como digitar aleatoriamente e formar uma palavra, (quase) certamente acontecem em um espaço de tempo infinito (a expressão “quase certamente” possui um significado matematicamente preciso e compreendido melhor dentro da teoria da probabilidade, para a qual Borel fez enormes contribuições).
Nesse exemplo, com tempo infinito para bater aleatoriamente nas teclas, o macaco acabará por escrever palavras, frases, parágrafos e até livros inteiros. Ele escreverá todas as obras de Shakespeare, mais de uma vez e de trás pra frente. Escreverá todos os roteiros de filmes da Marvel que já saíram e que ainda irão sair (embora esse seja outro infinito 😀).
Brincadeiras à parte, esse teorema não se limita a exemplos absurdos como um macaco com uma máquina de escrever, podendo ser observado em situações muito mais comuns.
Vamos considerar o número π, a clássica razão entre o comprimento da circunferência e seu diâmetro. Ele é um número irracional, com infinitas casas depois da vírgula dispostas sem nenhum padrão, aleatórias como o bater nas teclas do macaco. Podemos atribuir uma correspondência entre o conjunto dos caracteres disponíveis em um teclado e o conjunto de algarismos (ou sequências de algarismos) da expansão de π. Assim 01 poderia corresponder à letra “a”, 02 corresponderia a “b”, 27 ao algarismo “1”, e outras sequências poderiam corresponder a sinais de pontuação ou outros símbolos. Desse modo, poderíamos encontrar palavras escondidas na expansão decimal de π, mas não só isso!
Nesse sistema, na expansão de π provavelmente estão escritas todas as palavras e todas as frases em todas as línguas, seu nome aparece escrito infinitas vezes, a história de sua vida e a história do próprio universo! Tudo isso, dentro de um número entre 3 e 4.
É estranho pensar como esses infinitos que, apenas por existirem já desafiam todas as nossas concepções, abrangem concepções ainda mais complexas dentro de si, afinal essa Sala de Leitura sobre infinitos que você está lendo provavelmente nada mais é do que a cópia de algumas linhas da expansão de π.
VI – Alguns Vídeos Recomendados…
Se você se interessou pelo assunto e quiser saber mais a respeito, recomendamos aqui alguns vídeos que, inclusive, utilizamos de inspiração para compreender melhor os infinitos, suas dimensões e propriedades.
Alguns INFINITOS são MAIORES que outros
Este vídeo utiliza uma ótima analogia para explicar de maneira bastante didática porque o infinito dos naturais é tão grande quanto o dos naturais pares.
Para assistir, é só clicar na setinha.
Vídeo do canal “Ciência Todo Dia”, de Pedro Loss.
Os INFINITOS e a HIPÓTESE DO CONTÍNUO
O que é o infinito? Existe infinito no mundo real? Ou ele é apenas uma abstração, algo que existe apenas nas nossas mentes?
Para saber, é só clicar na setinha.
Vídeo do canal “Tem Ciência”, de Daniel Nunes.
Cardinalidade de Conjuntos
Para compreender um pouco melhor sobre cardinalidade de conjuntos, sugerimos que você assista aos vídeos sobre o assunto no canal Portal da Matemática OBMEP, começando pelo vídeo a seguir.
É só clicar na setinha.
COM Geomestres Slay (Colégio Militar de Porto Alegre, RS)
Equipe COM – OBMEP
Dezembro de 2023.
[1] Capítulo 2, Conjuntos Infinitos, por Martha Monteiro: IME-USP (Acesso em 02/12/2023).
[2] Filosofia da Física Clássica – USP 2017: FFLCH – USP (Acesso em 02/12/2023).
[3] Existe alguma coisa maior do que o infinito?, por Bruno Vaiano: Super Abril (Acesso em 02/12/2023).
[4] História do Infinito: Faculdade de Ciências da Universidade de Lisboa (Acesso em 02/12/2023).
[5] Conjuntos Enumeráveis e Não-Enumeráveis: Acervo digital- UFPR (Acesso em 02/12/2023).
[6] Um breve passeio ao infinito real de Cantor: UFPB (Acesso em 02/12/2023).
[7] Teorema do Macaco Infinito: Wikipédia (Acesso em 02/12/2023).