 |
Nesta sala vamos falar um pouquinho sobre multiplicação. |
|
Já entendi… |
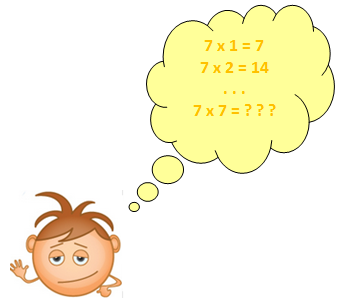 |
 |
Não se precipite… |
|
Raciocínio combinatório… |
 |
 |
Não é bem dessa combinação que estou falando e sim daquela que pode ser utilizada no nosso cotidiano para fazermos previsões e estimativas! |
Princípio Fundamental da Contagem
 |
Vamos resolver alguns problemas sobre possibilidades de escolha e, em seguida, apresentar um princípio essencial para a resolução desse tipo de problema. |
Raíza tem 2 calças e 3 camisetas de cores diferentes. Ela vai à escola de segunda a sexta, mas não quer repetir um mesmo conjunto de calça e camiseta na mesma semana.
Raíza conseguirá realizar seu desejo?
Solução:
● Se ela quer usar a primeira calça, pode combiná-la com qualquer uma das três camisetas, o que nos dá 3 visuais diferentes.
● Se ela usar a segunda calça, também vai poder combiná-la em 3 modelitos, um com cada camiseta.
O total de maneiras de combinar as peças é 3+3, ou seja, 2 × 3 = 6.
Então, Raíza conseguirá realizar o seu desejo de ir para a aula durante a semana sem repetir nenhum look, e ainda sobrará um look para o fim de semana…
Observações:
➊ No problema resolvido, Raíza tinha que escolher uma calça e uma camiseta para vestir. São duas escolhas ou decisões.
➋ Note que, se Raíza vestir qualquer uma das duas calças, isso não a impedirá de escolher entre três camisetas distintas. Para qualquer escolha da calça, há o mesmo número de escolha de camisetas.
➌ Como vimos, continuaremos com a mesma quantidade de possibilidades para a escolha da camiseta em cada escolha de calça. Então, podemos chegar à resposta multiplicando o número de calças pelo número de camisetas, obtendo assim os 2 × 3 = 6 looks possíveis.
➍ Sem comprometer a generalidade do problema, podemos supor “que Raíza tenha uma calça preta, uma calça branca e que suas camisetas sejam vermelha, amarela e verde” e, assim, visualizar a quantidade de looks possíveis, utilizando o diagrama abaixo.
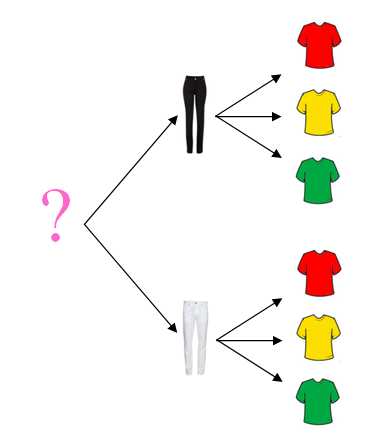
Esse tipo de diagrama é conhecido como diagrama de árvore.
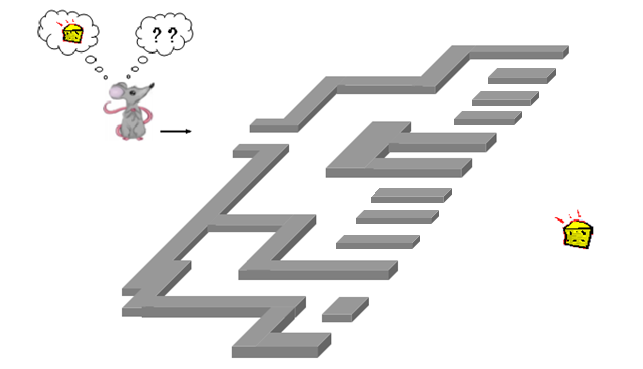
Solução:
Assim que entra no labirinto, o ratinho se depara com a necessidade de escolher um dentre 2 caminhos.
Quando ele segue qualquer um dos dois caminhos, depara-se com 4 outras possibilidades de caminho e precisa escolher um. Percorrido o caminho escolhido, ele encontra o queijo.
Perceba, então, que a quantidade total de possibilidades para o percurso a ser seguido é 2 x 4=8.
Ele os quer em forma de hexágonos regulares, com um pequeno círculo em seu interior.
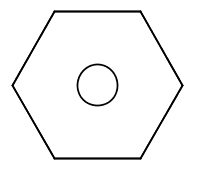 O rei dispõe, segundo suas preferências pessoais, de 3 cores distintas para pintar o hexágono e de 4 cores distintas para pintar o círculo. Sabendo que as duas formas (hexágono e círculo) serão unicolores, quantas são as opções para o novo modelo de azulejo?
O rei dispõe, segundo suas preferências pessoais, de 3 cores distintas para pintar o hexágono e de 4 cores distintas para pintar o círculo. Sabendo que as duas formas (hexágono e círculo) serão unicolores, quantas são as opções para o novo modelo de azulejo?
Solução:
Para cada uma das cores escolhidas para o hexágono, haverá 4 opções de cores para o círculo. Portanto, para cada opção de cor a ser utilizada no hexágono, há 4 azulejos possíveis. Como temos 3 opções de cores para o hexágono, há 3 × 4=12 opções para o azulejo do rei Tim.
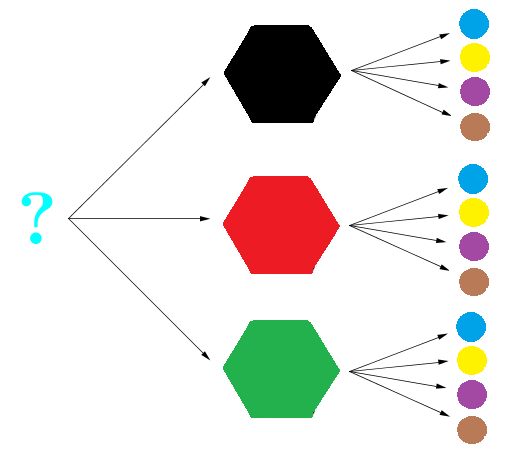
Podemos elucidar nossa solução utilizando um diagrama de árvore que ilustra todas as possibilidades. Suponha que as cores selecionadas para o hexágono sejam “preto”, “vermelho” e “verde”, enquanto as cores selecionadas para o círculo são “azul”, “amarelo”, “roxo” e “marrom”. (Observe que a solução será a mesma para quaisquer opções de cores. Elas foram nomeadas, apenas, para facilitar o seu entendimento.)
Teremos, assim, as possibilidades ilustradas pelo diagrama a seguir.
 |
A essa altura, já podemos enunciar o Princípio Multiplicativo ou Princípio Fundamental da Contagem (PFC). Ele é extremamente útil quando o número de possibilidades é grande e o diagrama de árvore se torna muito, mas muito cansativo mesmo…. |
Princípio Multiplicativo – Princípio Fundamental da Contagem
Se uma decisão A pode ser tomada de m maneiras distintas e, tomada essa decisão A, uma decisão B puder ser tomada de n maneiras distintas, então a quantidade de maneiras de se tomar sucessivamente as decisões A e B é igual a m x n.
Numa reunião havia 6 professores do Mato Grosso do Sul e 7 do Ceará.
Quando o grupo se reuniu, cada professor do Mato Grosso do Sul cumprimentou cada professor do Ceará exatamente uma vez.
Quantos cumprimentos ocorreram?
Solução:
Como cada cumprimento aconteceu entre um professor do Mato Grosso do Sul e um professor do Ceará, o total de cumprimentos é o total de maneiras de se escolher um professor do Mato Grosso do Sul e um do Ceará, simultaneamente.
Pelo Princípio Multiplicativo, o total é 6 x 7, ou seja, 42 cumprimentos.
 |
Os problemas a seguir são para você pensar: tente resolvê-los sem ver as soluções. |
Problemas Propostos
Quantos são os números naturais de 2 algarismos?
Problema 2:
Quantos são os números ímpares entre 10 e 99 (incluindo o 99)?
Problema 3:
A senha secundária de um banco imaginário é composta por uma vogal e uma consoante, nessa ordem, ambas provenientes do nome do cliente. Qual cliente terá mais opções de senha, o senhor Darli Munhoz ou o senhor Thiago Bruce?
Problema 4:
Considere que o ratinho do problema II, além de escolher entre os 8 caminhos, tivesse que escolher entre 4 tipos diferentes de queijo. Qual seria o total de maneiras de ele agir?
Problema 5:
E se a Raíza, do problema I, além das 6 possíveis combinações de blusa e saia, tivesse ainda 4 chapéus diferentes? Quantos looks ela poderia montar?
|
Mas espera um pouco… |
 |
 |
Isso mesmo! |
|
Hum…. |
 |
– Francimar de Brito Vieira
– Noemi Zeraick Monteiro
– Sonia Regina Di Giacomo
◆ Equipe COM – OBMEP
– Victor de Oliveira Bitarães
◆ Colaborador
 |
Ficaram curiosos? |
