✏ Link da Sala para dispositivos da Apple.
a1 , a2 , a3 , ⋅⋅⋅ , an
b1 , b2 , b3 , ⋅⋅⋅ , bm , ⋅⋅⋅
Sequências numéricas são objetos matemáticos importantes, pois permitem a modelagem matemática de fenômenos naturais e sociais, além de serem ferramentais fundamentais dentro da própria Matemática. Particularmente, possuem aplicações no campo da Computação, da Medicina, da Economia, das Engenharias, etc.
➤ Na Computação, as sequências numéricas podem ser utilizadas em algoritmos de busca e ordenação de dados, como por exemplo, o “Algoritmo de busca binária”. Esse algoritmo faz uso de uma sequência ordenada a fim de encontrar um elemento específico com eficiência e, para isso, ele divide por várias vezes uma sequência em duas metades, até que seja encontrado o elemento desejado ou que se conclua que esse elemento não está na sequência.
➤ Na Economia, sequências de preços num dado período são utilizadas em análises de tendências de alta ou baixa, de sazonalidade e também de variações cíclicas.
➤ As sequências podem ser utilizadas na introdução à análise de sinais. A análise de sinais e sistemas de controle são tópicos importantes e muito estudados na Engenharia Elétrica.
➤ Em Matemática Financeira, sequências numéricas são utilizadas para a obtenção do montante de um valor capitalizado periodicamente ou para o estudo de taxas de juros, financiamentos e prestações.
Nesta Sala estudaremos dois tipos particulares de sequências, as chamadas de Progressões Aritméticas e de Progressões Geométricas.
Um pouco de história
As sequências numéricas têm uma forte conexão com os processos de contagem e com a evolução dos sistemas de numeração. Vários registros de problemas relacionados a diferentes tipos de sequências podem ser encontrados nos principais documentos das civilizações antigas.
Acredita-se que o primeiro registro tenha ocorrido há cerca de 5.000 anos no Egito, quando surgiu a necessidade de se estabelecer padrões, como o das enchentes do Rio Nilo. Os egípcios necessitavam conhecer o período de inundação para poderem plantar na época adequada e, consequentemente, assegurar seus alimentos. Era necessário conhecer o padrão desse acontecimento.
 Imagem extraída de AVENTURAS NA HISTÓRIA (Acesso em dezembro de 2023.)
Imagem extraída de AVENTURAS NA HISTÓRIA (Acesso em dezembro de 2023.)
Ao perceberem que o nível do Rio Nilo aumentava logo após o surgimento da estrela Sírius no horizonte leste e notarem que isso se repetia a cada 365 dias, os antigos egípcios desenvolveram um calendário solar consistindo de doze meses, com cada mês contendo 30 dias, além de cinco dias de celebrações dedicadas aos deuses. Eles dividiram esses doze meses em três estações, cada uma com quatro meses: uma para semear, outra para o crescimento e a última para a colheita.
Há aproximadamente 6.000 anos, a civilização Babilônica habitava a região da Mesopotâmia. Foi descoberto pelos pesquisadores registros escritos dessa sociedade em tijolos feitos de argila, que eram relativamente finos. A escrita era realizada ao utilizar um tipo de estilete nos tijolos que ainda estavam úmidos. A escrita cuneiforme dos babilônios recebe esse nome devido aos seus traços que possuíam o formato de cunha. Foram encontrados por arqueólogos tabletes babilônicos que provavelmente datam de 1.800 a.C. Esses tabletes apresentam as sequências numéricas “1, 3, 9, 27, 81, …” e “1, 4, 16, 64, …”.
Na civilização grega, existem muitos exemplos de sequências numéricas. Alguns desses exemplos são as sequências estudadas pela escola pitagórica por volta do século VI a.C., que envolviam números figurados e o Crivo de Eratóstenes que pode ser utilizado, por exemplo, para obter a sequência dos números primos.
Várias figuras históricas trabalharam, direta ou indiretamente, com sequências numéricas. Entre eles destacamos:
● Zenão de Eleia, filosofo grego que viveu entre, aproximadamente, 490 e 425 a.C., famoso por propor paradoxos que desafiaram matemáticos por muitos séculos.
● Arquimedes de Siracusa, considerado o maior matemático de sua época. Suas contribuições na geometria revolucionaram o assunto e seus métodos anteciparam o hoje chamado “Cálculo Integral”. Viveu de 287 a 212 a.C., aproximadamente.
● Leonardo de Pisa, mais conhecido como Fibonacci, viveu de 1170 a 1250. Com seu livro Liber abaci, introduziu o sistema decimal hindu-arábico com valor posicional e o uso de algarismos arábicos na Europa.
● Carl Friedrich Gauss, conhecido como “o Príncipe da Matemática” , viveu de 1777 a 1855. É considerado o maior matemático do século XIX e, ao lado de Arquimedes e Isaac Newton, como um dos maiores de todos os tempos! Trabalhou em uma ampla variedade de campos da Matemática e da Física; seu trabalho teve imensa influência em muitas áreas.

Imagens extraídas de MacTutor History of Mathematics archive (Acesso em dezembro de 2023)
Introdução
Como já mencionamos anteriormente, nosso objetivo principal é o estudo de dois tipos de sequências, as Progressões Aritméticas e as Progressões Geométricas; mas, antes, precisaremos ver alguns conceitos básicos comuns a todos os tipos de sequências numéricas.
Inicialmente, considere a seguinte situação:
| número do lançamento | face obtida |
| 1 | 2 |
| 2 | 5 |
| 3 | 1 |
| 4 | 1 |
| 5 | 6 |
| 6 | 3 |
| 7 | 5 |
A relação existente entre o número do lançamento e o número da face obtida define uma função. De fato, a cada lançamento feito podemos associar um único número, que corresponde à face voltada para cima, no dado. Em tal função, o domínio é {1, 2, 3, 4, 5, 6, 7}, o contradomínio é também {1, 2, 3, 4, 5, 6, 7} e conjunto imagem é {1, 2, 3, 5, 6}.
Observe, agora, que poderíamos apresentar os números obtidos em cada lançamento, ordenando-os de acordo com a ordem na qual eles foram obtidos e utilizando uma notação especial: (2, 5, 1, 1, 6, 3, 5).
Essa função que definimos é um exemplo de sequência numérica finita e a maneira pela qual representamos os resultados é como, na prática, representaremos nossas sequências.
Vamos formalizar essas ideias!
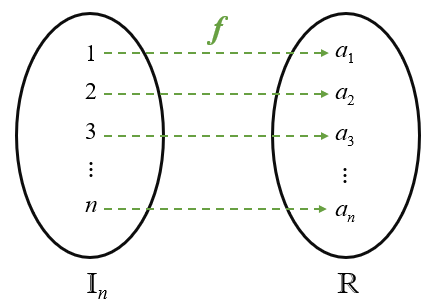
[tex]f:I_n=\{1,2,3,⋯,n\}\rightarrow \mathbb{R}.[/tex]
Para todo [tex]i \in I_n[/tex], o valor [tex]f(i)[/tex] será representado por [tex]a_i[/tex] e denominado o i-ésimo termo da sequência.
De forma semelhante, definimos sequências numéricas infinitas.
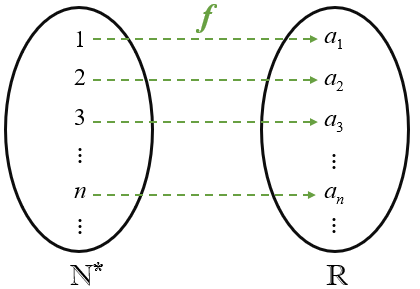
[tex]f:\mathbb{N}^*=\{1,2,3,⋯\}\rightarrow \mathbb{R}.[/tex]
Para todo [tex]i \in \mathbb{N}^*[/tex], o valor [tex]f(i)[/tex] será igualmente representado por [tex]a_i[/tex] e também denominado o i-ésimo termo da sequência.
Embora matematicamente falando “sequências sejam funções”, vamos utilizar uma notação que nos permitirá pensar em uma sequência numérica como uma “lista de números ordenados”.
➤ As sequências finitas, da forma que foram definidas acima, serão denotadas por
[tex]\qquad \qquad \left(a_i\right)_{i\in I_n}=(a_1,~a_2,~a_3,~ \cdots~,~a_n)[/tex]
ou simplesmente
[tex] \qquad \qquad \left(a_i\right)=\left(a_1,~a_2,~a_3,~ \cdots~,~a_n\right)[/tex]
[tex] \qquad \qquad \left(f\right)=\left(a_1,~a_2,~a_3,~ \cdots~,~a_n\right).[/tex]
➤ As sequências infinitas, da forma que foram definidas acima, serão denotadas por
[tex] \qquad \qquad \left(a_i\right)_{i\in\mathbb{N}^*}=\left(a_1,~a_2,~a_3,~ \cdots~,~a_n,~ \cdots~\right)[/tex]
ou simplesmente
[tex] \qquad \qquad \left(a_i\right)=\left(a_1,~a_2,~a_3,~ \cdots~,~a_n, ~\cdots~\right)[/tex]
[tex] \qquad \qquad \left(f\right)=\left(a_1,~a_2,~a_3,~ \cdots~,~a_n, ~\cdots~\right).[/tex]
Exemplos:
● (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10) é a sequência dos onze primeiros números naturais.
● (0, 2, 4, 6, 8) é a sequência dos cinco primeiros números naturais pares.
● (2, 3, 5, 7, 11, 13, 17, 19, 23) é a sequência dos nove primeiros números naturais primos.
● (1, 3, 5, 7, 9, 11, ⋅ ⋅ ⋅) é a sequência dos números naturais ímpares.
● (0, 5, 10, 15, 20, 25, 30, 35, ⋅ ⋅ ⋅ ) é a sequência dos números naturais múltiplos de 5.
● (3; 3,1; 3,14; 3,141; 3,1415; 3,14159; 3,141592; 3,1415926; ⋅ ⋅ ⋅) é a sequência dos números decimais em que cada termo se aproxima de [tex]\pi[/tex] uma casa decimal a mais que o termo anterior.
Observação: Você deve ter notado que no último exemplo os termos da sequência foram separados por “;”. Na verdade, faremos isso sempre que alguns termos de uma sequência forem números decimais, para evitarmos confusões sobre quais são os termos da sequência numérica.
Lei de formação
Observe as duas sequências a seguir:
● ( f ) = (0, 3, 6, 9, 12, 15, 18, 21, 24,?);
● ( g ) = (1500, 7, 2, 939, 512, 1, 1, 749871, 24,?).
Sem muito esforço, você consegue prever que 27 é o número que sucede o 24 na primeira sequência, não é? Mas qual é o número que sucede o 24 na segunda? Impossível determinar…
Isso acontece porque na primeira sequência os termos são definidos por uma regrinha, o que parece não acontecer com a segunda sequência. Esses dois exemplos ilustram que apenas listar alguns termos de uma sequência não é suficiente para que identifiquemos e tenhamos certeza de qual é a sequência que estamos trabalhando, de fato. Sem uma regra, nada impede que o último termo da primeira sequência seja 47, ou 61 ou 1578, embora pareça ser 27…
Quando existe, a regra que define o valor de cada termo de uma sequência é chamada de lei de formação e, conforme já pudemos observar, nem toda sequência possui, obrigatoriamente, uma lei de formação.
Assim, quando existe, a lei de formação de uma sequência é a regra que estabelece a formação dos termos dessa sequência. A partir da lei de formação, também conhecida como fórmula do termo geral, é possível obter qualquer termo da respectiva sequência numérica.
As leis de formação que dão origem às sequências numéricas podem ser apresentadas, essencialmente, de três maneiras:
– Por uma propriedade que expressa cada termo da sequência em função da sua posição.
– Por uma fórmula de recorrência.
– Por uma propriedade dos termos.
Trataremos, a seguir, de cada um desses tipos de regras.
(1) Expressando cada termo em função da posição: Nesta lei de formação, o termo [tex]a_n[/tex] de uma sequência é obtido por meio de uma fórmula definida em função de [tex]n.[/tex]
Exemplos:
Podemos montar uma tabela com os valores dos primeiros termos da sequência:
[tex]~~~~~~~~~~~~~~~~~~~~~~\begin {array}{|c| c|}
\hline
n & a_n \\
\hline
1 & a_1 = 1^2 = 1 \\
\hline
2 & a_2 = 2^2=4\\
\hline
3 & a_3 = 3^2 = 9\\
\hline
4 & a_4 = 4^2 =16\\
\hline
5 & a_5 = 5^2=25\\
\hline
\end{array}[/tex]
Portanto, a sequência é [tex](a_n)=(1,4,9,16,25,\cdots ).[/tex]
Podemos montar uma tabela com os valores de todos os termos da sequência:
[tex]~~~~~~~~~~~~~~~~~~~~~~\begin {array}{|c| c|}
\hline
n & b_n \\
\hline
1 & b_1 = 3^1 = 3 \\
\hline
2 & b_2 = 3^2=9\\
\hline
3 & b_3 = 3^3 = 27\\
\hline
4 & b_4 = 3^4 =81\\
\hline
\end{array}[/tex]
Portanto, temos a sequência [tex](b_n)=(3,9,27,81).[/tex]
(2) Fórmula de recorrência: A fórmula de recorrência é uma regra que relaciona cada termo da sequência com termos antecessores.
A maneira mais simples de apresentar uma relação de recorrência é definir o termo [tex]a_n[/tex] a partir do termo [tex]a_{n-1}[/tex] e definir o primeiro termo da sequência. Mas, existem sequências apesentadas por fórmulas de recorrência que possuem leis de formação “mais elaboradas”, nas quais cada termo pode ser obtido utilizando-se mais de um termo imediatamente anterior e vários termos iniciais são explicitamente apresentados.
Exemplos:
Podemos encontrar recorrentemente cada termo da sequência, conforme segue:
[tex]\quad b_1 = 2[/tex];
[tex]\quad b_2 = 3\cdot b_1-1=3\cdot 2-1=5[/tex];
[tex]\quad b_3=3\cdot b_2-1=3\cdot 5-1=14[/tex];
[tex]\quad b_4=3\cdot b_3-1=3\cdot 14-1=41[/tex];
[tex]\quad b_5=3\cdot b_4-1=3\cdot 41-1=122[/tex].
Portanto, a sequência em questão é [tex](b)=(2, 5, 14, 41, 122).[/tex]
Podemos encontrar os termos iniciais da sequência, conforme segue:
[tex]\quad a_1 = 1[/tex];
[tex]\quad a_2 = 1[/tex];
[tex]\quad a_3=a_2+a_1 = 1+1=2[/tex];
[tex]\quad a_4=a_3+a_2 = 2+1=3[/tex];
[tex]\quad a_5=a_4+a_3 = 3+2=5[/tex];
[tex]\quad a_6=a_5+a_4 = 5+3=8[/tex];
[tex]\quad a_7=a_6+a_5 = 8+5=13[/tex];
[tex]\quad a_8=a_7+a_6 = 13+8=21[/tex];
[tex]\quad a_9=a_8+a_7 = 21+13=34[/tex];
[tex]\quad a_{10}=a_9+a_8 = 34+21=55[/tex].
Com isso, temos a sequência [tex](1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \cdots);[/tex] que é conhecida como sequência de Fibonacci. Fibonacci a utilizou na sua obra Liber abaci para descrever o crescimento da seguinte população de coelhos, ao longo do tempo: um casal de coelhos reproduz um novo casal a cada mês; cada casal gerado reproduz um novo casal em dois meses após seu nascimento, e assim por diante.
A sequência de Fibonacci é muito utilizada atualmente nos campos da Ciência da Computação, da Teoria de Jogos, no Mercado Financeiro, na Biologia, dentre outras áreas.
(3) Propriedade dos termos: Com esta Lei de Formação, os termos de uma sequência são obtidos a partir de alguma propriedade que deve ser apresentada.
Exemplos:
Vamos encontrar a quantidade de divisores positivos de cada um dos números de [tex]1[/tex] a [tex]8[/tex]:
divisores positivos de 1: 1 (1 número);
divisores positivos de 2: 1, 2 ( 2 números);
divisores positivos de 3: 1, 3 ( 2 números);
divisores positivos de 4: 1, 2, 4 ( 3 números);
divisores positivos de 5: 1, 5 ( 2 números);
divisores positivos de 6: 1, 2, 3, 6 ( 4 números);
divisores positivos de 7: 1, 7 ( 2 números);
divisores positivos de 8: 1, 2, 4, 8 ( 4 números);
Portanto, a sequência encontrada é (1, 2, 2, 3, 2, 4, 2, 4).
Outras Salas
Nas duas próximas salas, estudaremos dois tipos especiais de sequências e, na última, disponibilizaremos alguns problemas e suas soluções.
Sala 1: Progressão Aritmética
Sala 2: Progressão Geométrica
Sala 3: Problemas
Essas Salas podem ser acessadas clicando-se em um dos botões abaixo. Em qualquer uma delas, você encontrará um link para voltar para esta Sala, na parte inferior à direita da página.
Equipe COM – OBMEP
Janeiro de 2024.
[1] CARVALHO, Maria Cecília Costa e Silva. Padrões Numéricos e Sequências. São Paulo: Editora Moderna, 1997.
[2] IEZZI G.; DOLCE O.; DEGENSZAJN D.; PÉRIGO R.; ALMEIDA N. Matemática ciências e aplicações 1: conecte live. São Paulo: Saraiva, 2018.
[3] Johann Carl Friedrich Gauss – Clubes (Acesso em 23/12/2023).
[4] Progressões: Progressão Geométrica – Guia do Estudante (Acesso em 23/12/2023).
[5] Várias páginas – MacTutor History of Mathematics archive (Acesso em 23/12/2023).
