A Função Probabilidade
|
Como a conhecemos atualmente, a teoria matemática das probabilidades é recente; o seu estudo é feito a partir dos axiomas de Andrei Kolmogorov (1903-1987), matemático russo cujo trabalho influenciou vários ramos da Matemática, especialmente a Análise Harmônica, a Teoria de Conjuntos, a Teoria da Informação, a Teoria dos Números e, é claro, a Teoria da Probabilidade. A amplitude da produção criativa de Kolmogorov pode ser medida pelos mais de 500 artigos e livros que ele publicou entre 1923 e 1977. Nesta Sala, vamos apresentar a definição da chamada Função Probabilidade e explorar algumas de suas características e propriedades. Essa definição foi estabelecida por Kolmogorov na forma de uma definição axiomática em seu trabalho publicado em 1933 e intitulado Grundbegriffe der Wahrscheinlichkeitsrechnung (que em inglês ficou conhecido como Foundations of Probability Theory – Fundamentos da Teoria da Probabilidade). Com esse trabalho, tem início a etapa moderna da Teoria da Probabilidade: a Teoria da Probabilidade construída de forma rigorosa a partir de axiomas fundamentais, semelhante ao tratamento da Geometria de Euclides. |
 Andrey Kolmogorov |
Definição axiomática de Probabilidade
Sabemos que na análise de um experimento aleatório, é necessário atribuir para cada evento [tex]A[/tex] do espaço amostral [tex]\Omega[/tex] um número que nos dê uma indicação quantitativa da possibilidade de esse evento ocorrer. Ao longo da nossa discussão denotaremos esse número por [tex]P(A)[/tex].
Para satisfazer a definição matemática de probabilidade apresentada abaixo, o número [tex]P(A)[/tex] precisa cumprir três condições específicas. São essas condições que assegurarão que [tex]P(A)[/tex] terá as propriedades intuitivas esperadas por alguém que conheça exemplos particulares de probabilidades.
Uma probabilidade (ou uma medida de probabilidade) em [tex]\Omega[/tex] é uma função que associa a cada evento [tex]A[/tex] de [tex]\Omega[/tex] um número [tex]P(A)[/tex], denominado probabilidade de [tex]A[/tex], de forma que:
[tex]\textcolor{#8b4513}{(i)}\; 0 \leq P(A) \leq 1[/tex], para todo [tex]A \subset \Omega[/tex];
[tex]\textcolor{#8b4513}{(ii)}\; P(\Omega) = 1[/tex];
[tex]\textcolor{#8b4513}{(iii)}\;[/tex] Se [tex]A[/tex] e [tex]B[/tex] são eventos de [tex]\Omega[/tex] mutuamente excludentes ([tex]A \cap B=\emptyset[/tex]), então [tex]P(A \cup B) = P(A) + P(B)[/tex].
Neste caso, o par ordenado [tex]\left(\Omega,P\right)[/tex] é denominado um Espaço de Probabilidades.
Observação: Como [tex]\boxed{0 \leqslant P(A) \leqslant 1}[/tex], podemos utilizar porcentagem para expressar a probabilidade de um evento [tex]A[/tex]. Neste caso, lembre-se de multiplicar o número [tex]P(A)[/tex] por [tex]100[/tex] ou de utilizar uma regra de três.
A princípio, alguém que termine a leitura da definição geral que acabamos de apresentar pode se perguntar:
– Os números que vamos atribuir aos eventos de um experimento aleatório devem satisfazer as três condições apresentadas na definição. Mas que números são esses?
A definição em si não estabelece qual é a função probabilidade que devemos associar a um dado experimento aleatório. Conforme já anunciamos, vamos apresentar nos nossos estudos três modelos diferentes de probabilidade, com suas respectivas funções particulares. Mas agora, vamos tentar entender como é que funciona essa definição geral que acabamos de anunciar. Antes de mais nada, convém observar que sobre um mesmo espaço amostral é possível se definir várias funções probabilidades; veja o próximo exemplo.
Consideremos o experimento já descrito anteriormente do lançamento de uma moeda e a verificação se, depois da queda, a face voltada para cima é cara ou coroa.
Iremos estabelecer três funções definidas para os subconjuntos do espaço amostral [tex]\Omega=\{[/tex]cara , coroa[tex]\}[/tex], [tex]P_1[/tex], [tex]P_2[/tex] e [tex]P_3[/tex], e verificar quais delas podem ser chamadas de função probabilidade.
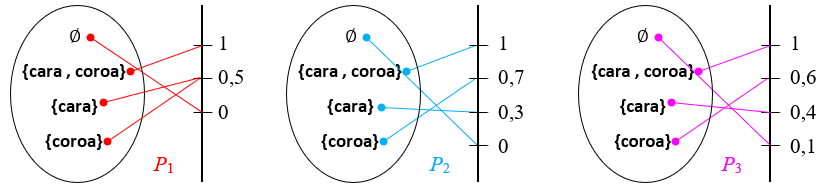
[tex]\textcolor{#8b4513}{(i)}\;[/tex] Observe que:
► as imagens definidas por [tex]P_1[/tex] são [tex]0;\, 0,5;\, 1[/tex];
► as imagens definidas por [tex]P_2[/tex] são [tex]0;\, 0,3;\,0,7;\, 1[/tex];
► as imagens definidas por [tex]P_3[/tex] são [tex]0,1;\, 0,4;\,0,6;\, 1[/tex];
assim, as três funções atendem à condição [tex]\textcolor{#8b4513}{(i)}\,.[/tex]
[tex]\textcolor{#8b4513}{(ii)}\;[/tex] Como:
► [tex]P_1\left(\Omega\right)=1[/tex];
► [tex]P_2\left(\Omega\right)=1[/tex];
► [tex]P_3\left(\Omega\right)=1[/tex];
as três funções atendem à condição [tex]\textcolor{#8b4513}{(ii)}\,.[/tex]
[tex]\textcolor{#8b4513}{(iii)}\;[/tex] Resta então verificar quais delas atendem à última condição da definição. Aqui vale ressaltar que essa condição só é satisfeita se verificarmos a sua validade para todo par de eventos disjuntos. Se um par de eventos disjuntos não obedecer a condição, isso já é suficiente para sabermos que a condição [tex]\textcolor{#8b4513}{(iii)}\;[/tex] não foi satisfeita.
No experimento em questão, os pares de eventos disjuntos são "[tex]\emptyset[/tex] e {cara}", "[tex]\emptyset[/tex] e {coroa}", "[tex]\emptyset[/tex] e {cara, coroa}" e "{cara} e {coroa}"; então, vamos lá!
Analisando a função [tex]P_1[/tex]:
► Como [tex]E \cup \emptyset = E[/tex] e [tex]P_1(\emptyset) = 0[/tex], temos que:
[tex]\quad \quad \boxed{P_1(E \cup \emptyset)} = P_1(E) = P_1(E) + 0 = \boxed{P_1(E) + P_1(\emptyset)}[/tex],
[tex]\quad \quad[/tex] para todo evento [tex]E \subset \Omega\,.[/tex]
► Como [tex]\{cara \} \cup \{coroa \} = \Omega[/tex], temos:
[tex]\quad \quad \begin{align*}\boxed{P_1(\{cara \} \cup \{coroa \})} &= P_1(\Omega) = 1 = 0,5 + 0,5 \\
&=\boxed{P_1(\{cara \}) + P_1(\{coroa \})}\,.\end{align*}[/tex]
Assim, [tex]P_1[/tex] satisfaz a condição [tex]\textcolor{#8b4513}{(iii)}\;[/tex] e, portanto, é uma função probabilidade para [tex]\Omega\,.[/tex]
Analisando a função [tex]P_2[/tex]:
► Aqui também, se [tex]E \subset \Omega\,[/tex], então [tex]E \cup \emptyset = E[/tex].
Assim, como [tex]P_2(\emptyset) = 0[/tex], temos que:
[tex]\quad \quad \boxed{P_2(E \cup \emptyset)} = P_2(E) = P_2(E) + 0 = \boxed{P_2(E) + P_2(\emptyset)}\,.[/tex]
► Por outro lado, como [tex]\{cara \} \cup \{coroa \} = \Omega[/tex], segue que:
[tex]\quad \quad \quad \quad \begin{align*}\boxed{P_2(\{cara \} \cup \{coroa \})}& = P_2(\Omega) = 1 = 0,3 + 0,7\\
& = \boxed{P_2(\{cara \}) + P_2(\{coroa \})}\,.\end{align*}[/tex]
Assim, [tex]P_2[/tex] satisfaz a condição [tex]\textcolor{#8b4513}{(iii)}\;[/tex] e, portanto, também é uma função probabilidade para [tex]\Omega\,.[/tex]
Analisando a função [tex]P_3[/tex]:
Observe que:
[tex]\qquad P_3(\{cara \} \cup \emptyset) = P_3(\{cara \}) = 0,4[/tex]
e
[tex]\qquad P_3(\{cara \}) + P_3(\emptyset) = 0,4 + 0,1 = 0,5[/tex].
Logo, [tex]P_3[/tex] não satisfaz a condição [tex]\textcolor{#8b4513}{(iii)}\;[/tex] e, portanto, NÃO é uma função probabilidade, embora satisfaça as condições [tex]\textcolor{#8b4513}{(i)}\,[/tex] e [tex]\,\textcolor{#8b4513}{(ii)}\,.[/tex]
Observação: Com certeza, a função [tex]P_1[/tex] é o tipo de probabilidade que a maioria das pessoas associam ao experimento do lançamento de uma moeda para a verificação se, depois da queda, a face voltada para cima é cara ou coroa. Mas com esse exemplo já percebemos que pode existir mais de um tipo de probabilidade associada a um fixado experimento aleatório!
Uma vantagem de se trabalhar matematicamente a partir de um conceito geral é que as propriedades que esse conceito satisfaz são resultados satisfeitos pelos casos particulares desse conceito geral. Dessa forma, vamos ver algumas propriedades da função probabilidade, com a certeza de que cada uma delas poderá ser utilizada nos estudos específicos dos casos particulares de probabilidade que iremos fazer nesta Sala.
 |
Se vocês precisarem de uma ajuda com as propriedades de conjuntos e com Diagramas de Venn, visitem esta Sala. |
Propriedades
Sejam [tex]A[/tex] e [tex]B[/tex] eventos de um mesmo experimento com espaço amostral [tex]\Omega[/tex]. Se [tex]P[/tex] é uma função probabilidade qualquer, então
(1) [tex]P(\emptyset) = 0\,.[/tex]
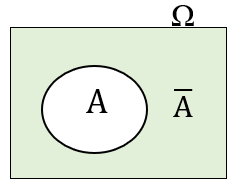
(2) [tex]P(\overline{A}) = 1-P(A)\,.[/tex]
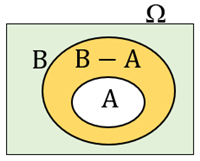
(3) Se [tex]A \subset B[/tex] então [tex]P(A)=P(B)-P(B-A)\,.[/tex]
(4) Se [tex]A \subset B[/tex] então [tex]P(A) \leqslant P(B)\,.[/tex]
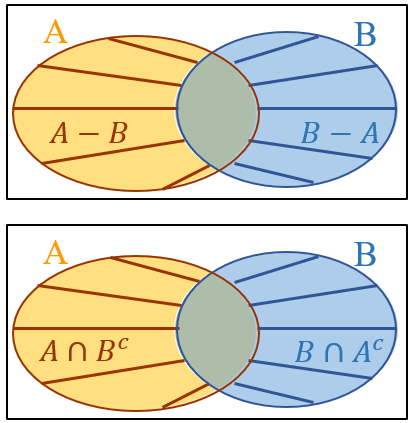
(5) [tex]P(A \cup B) = P(A) + P(B)-P(A \cap B)\,.[/tex]
(6) [tex]P(A-B) = P(A)-P(A \cap B)\,.[/tex]
Vamos apresentar mais dois exemplos que envolvem a utilização da definição e das propriedades apresentadas. Lembre-se de que as condições da definição e as propriedades devem ser satisfeitas por qualquer modelo de Espaço de Probabilidades que defina explicitamente como atribuir probabilidades aos seus eventos.
►[tex]P(A\cup B)[/tex]; [tex]P(\overline{A})[/tex]; [tex]P(\overline{B})[/tex]; [tex]P(A \cap \overline{B})[/tex]; [tex]P(\overline{A}\cap B)[/tex]; [tex]P(\overline{A} \cap \overline{B})[/tex]; [tex]P(\overline{A} \cup \overline{B})[/tex].
Que tal resolvermos alguns problemas definindo probabilidades e utilizando as propriedades que apresentamos?

A tabela abaixo dá a probabilidade de que um doce da confeitaria escolhido aleatoriamente tenha uma determinada cor, com exceção do valor relativo aos doces marrons.
[tex]\begin{array}{|c|c|c|c|c|c|}
\hline
\text{Branco}&\text{Vermelho}&\text{Amarelo}&\text{Verde}&\text{Laranja}&\text{Marrom}\\
\hline
0,3&0,2&0,2&0,1&0,1&\\
\hline
\end{array}[/tex]
(a) Qual deve ser o valor da probabilidade não apresentada?
(b) Se você tirar um doce aleatoriamente de um pacote, qual é a probabilidade de cada um dos eventos abaixo?
(b1) Você obtém um doce branco ou um vermelho.
(b2) Você não obtém um doce amarelo.
(b3) Você não obtém um doce laranja ou marrom.
(b4) Você retira um doce que é branco, vermelho, amarelo, verde, laranja ou marrom.
Um paciente chega a um consultório médico com dor de garganta e febre baixa.

Imagem extraída de Vecteezy
Depois de um exame, o médico conclui que o paciente tem uma infecção bacteriana ou uma infecção viral ou ambas. O médico atribui probabilidade [tex]0,7[/tex] para a infecção bacteriana e [tex]0,5[/tex] para a infecção viral.
(a) Qual a probabilidade de o paciente ter as duas formas de infecção?
(b) Qual a probabilidade de o paciente ter somente a infecção bacteriana?
(c) Qual a probabilidade de o paciente ter somente a infecção viral?
Luiz e Antônio foram assistir a uma corrida de cavalos e o Luiz resolveu fazer uma aposta. Antônio, que se diz um especialista em corridas de cavalos, passou ao Luiz as seguintes informações: dos dezesseis cavalos que participariam do páreo, o cavalo número [tex]5[/tex] teria uma probabilidade de [tex]0,3[/tex] de ganhar; os cavalos [tex]8[/tex] e [tex]11[/tex] teriam cada um [tex]0,2 [/tex] de probabilidade de ganhar e cada um dos demais cavalos teria probabilidade [tex]0,05[/tex] de vencer, exceto o número [tex]13[/tex] que é o cavalo com menor probabilidade de ganhar.

Imagem extraída de Freepik
O que podemos dizer sobre os conselhos do Antônio?
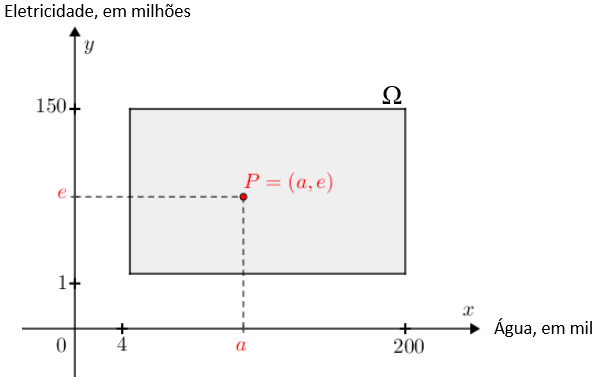
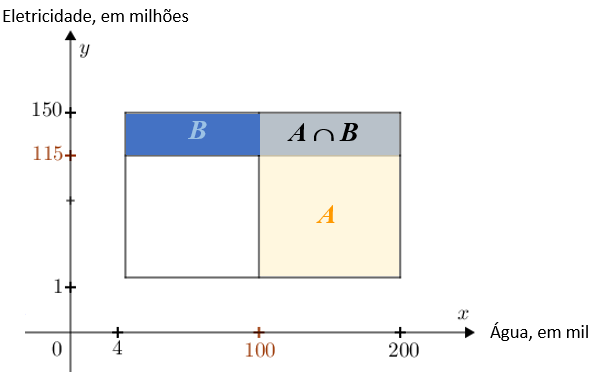
Uma construtora está construindo um complexo de escritórios e precisa planejar a demanda de água e de eletricidade, a fim de especificar as dimensões dos canos, tubos, conduítes e cabos elétricos. Depois de consultar potenciais compradores e examinar dados de outras construções, o engenheiro responsável pelo projeto considera que a demanda de eletricidade variará entre [tex]1[/tex] milhão e [tex]150[/tex] milhões de kWh por dia e a demanda de água será entre [tex]4[/tex] e [tex]200[/tex] mil litros por dia.
(a) Defina um espaço amostral para o experimento de determinar todas as combinações de demanda diária de eletricidade e de água para o complexo de escritórios que será construído.
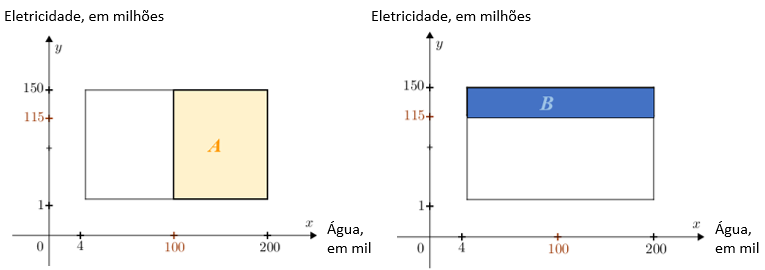
(b) Suponha que o engenheiro responsável esteja interessado em alta demanda. Seja [tex]A [/tex] o conjunto onde a demanda de água é de pelo menos [tex]100[/tex] mil litros diários, seja [tex]B [/tex] o evento em que a demanda elétrica é de pelo menos [tex]115 [/tex] milhões de KWH por dia e suponha que esses valores sejam considerados alta demanda. Represente esses eventos dentro do espaço amostral definido em (a).
(c) É possível atribuir probabilidades nesse modelo que utilizamos para representar as demandas diárias de eletricidade e de água para o complexo de escritórios que será construído?
A ideia de utilizar áreas no Problema 4 faz parte da chamada Probabilidade Geométrica, com a qual possíveis acontecimentos podem ser representados por pontos de um segmento de reta, por figuras planas ou ainda por sólidos.
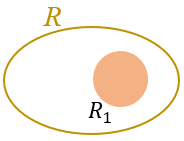 Na Probabilidade Geométrica, se tivermos uma região [tex]R_1[/tex] do plano contida em uma região [tex]R[/tex], admite-se que a probabilidade de um ponto de [tex]R[/tex] também pertencer a [tex]R_1[/tex] não depende da posição que [tex]R_1[/tex] ocupa em [tex]R[/tex]. Assim, escolhido ao acaso um ponto de [tex]R[/tex], a probabilidade [tex]p[/tex] de esse ponto pertencer a [tex]R_1[/tex] é definida por
Na Probabilidade Geométrica, se tivermos uma região [tex]R_1[/tex] do plano contida em uma região [tex]R[/tex], admite-se que a probabilidade de um ponto de [tex]R[/tex] também pertencer a [tex]R_1[/tex] não depende da posição que [tex]R_1[/tex] ocupa em [tex]R[/tex]. Assim, escolhido ao acaso um ponto de [tex]R[/tex], a probabilidade [tex]p[/tex] de esse ponto pertencer a [tex]R_1[/tex] é definida por
[tex]\qquad \qquad \boxed{p=\dfrac{\text{área de }R_1}{\text{área de }R}}\,.[/tex]
É bastante simples verificar que essa definição satisfaz as condições [tex]\textcolor{#8b4513}{(i)}\;[/tex], [tex]\textcolor{#8b4513}{(ii)}\;[/tex] e [tex]\textcolor{#8b4513}{(iii)}\;[/tex] da definição de função probabilidade, então podemos utilizá-la de fato como uma probabilidade.
Um atirador, com os olhos vendados, procura atingir um alvo circular com [tex]50\text{ cm}[/tex] de raio tendo no centro um disco com raio de [tex]20\text{ cm}[/tex]. Em um dado momento, finalmente o atirador acertou o alvo. Qual a probabilidade de que ele tenha atingido o disco central nesse lançamento?

Quebrando aleatoriamente um macarrão espaguete, de tamanho qualquer, em três partes, qual a probabilidade de que elas possam formar um triângulo?

A probabilidade de ocorrer um evento impossível é sempre nula. Mas, se a probabilidade de ocorrer um evento for igual a zero, esse evento é necessariamente impossível?
Agora é a vez de vocês!
Bons estudos!!!
Espaços amostrais finitos
Os experimentos mais simples para se definir probabilidades são aqueles que envolvem uma quantidade finita de resultados; pois saber a probabilidade de ocorrência de cada evento elementar de um espaço amostral finito nos permite calcular o valor da probabilidade de qualquer outro evento e, consequentemente, fica determinada a função probabilidade.
Em parte, a facilidade de se definir probabilidades em experimentos com quantidade finita de resultados é devida à propriedade que apresentaremos a seguir.
Propriedade
(7) Em um espaço amostral finito, a probabilidade de um evento com mais de um ponto amostral é a soma das probabilidades dos eventos elementares que estão contidos nesse evento.
Com efeito, considere um experimento aleatório cujo espaço amostral [tex]\Omega=\{a_1 , a_2, \ldots , a_n\}[/tex] tem [tex]n[/tex] elementos, tais que seus eventos elementares são [tex]E_1 = \{a_1\}[/tex], [tex]E_2 = \{a_2\}[/tex], [tex]\ldots[/tex], [tex]E_n = \{a_n\}[/tex] e suas respectivas probabilidades sejam [tex]p_1, p_2, \ldots, p_n[/tex].(Observe que, como [tex]\Omega[/tex] tem [tex]n[/tex] elementos, então [tex]a_i \ne a_j[/tex], para [tex]i\ne j\,.[/tex])
Se [tex]E = \{a_1, a_2 \}[/tex], a condição [tex]\textcolor{#8b4513}{(iii)}\;[/tex] da definição de função probabilidade nos garante que
[tex]\qquad P(E) = P(\{a_1, a_2 \})[/tex]
[tex]\qquad P(E) = P(\{a_1\} \cup \{a_2\})[/tex]
[tex]\qquad P(E) = P(\{a_1\}) + P(\{a_2\})[/tex]
[tex]\qquad \boxed{P(E) = p_1 + p_2}[/tex].
Vejamos como podemos calcular a probabilidade do evento [tex]E = \{a_1, a_2 , a_3\}[/tex], a partir da probabilidade dos eventos elementares.
[tex]\qquad P(E) = P(\{a_1, a_2 , a_3\})[/tex]
[tex]\qquad P(E) = P(\{a_1, a_2\} \cup \{a_3\})[/tex]
[tex]\qquad P(E) = P(\{a_1, a_2\}) + P(\{a_3\})[/tex] (usando a condição [tex]\textcolor{#8b4513}{(iii)}\;[/tex] da definição de função probabilidade)
[tex]\qquad P(E) = P(\{a_1\} \cup \{a_2\}) + P(\{a_3\})[/tex]
[tex]\qquad P(E) = p_1 + p_2 + P(\{a_3\})[/tex] (usando os cálculos anteriores)
[tex]\qquad \boxed{P(E) = p_1 + p_2 + p_3}[/tex].
Agora, se [tex]E = \{a_1, a_2 , a_3 , a_4 \}[/tex], então:
[tex]\qquad P(E) = P(\{a_1, a_2 , a_3 , a_4\})[/tex]
[tex]\qquad P(E) = P(\{a_1, a_2 , a_3\} \cup \{a_4\})[/tex]
[tex]\qquad P(E) = P(\{a_1, a_2 , a_3\}) + P(\{a_4\})[/tex] (usando a condição [tex]\textcolor{#8b4513}{(iii)}\;[/tex] da definição de função probabilidade)
[tex]\qquad P(E) = p_1 + p_2 + p_3 + P(\{a_4\})[/tex] (usando os cálculos anteriores)
[tex]\qquad P(E) = p_1 + p_2 + p_3 + p_4[/tex].
Da mesma forma, se [tex]E = \{a_1, a_2 , a_3 , a_4 , a_5 \}[/tex], então:
[tex]\qquad P(E) = P(\{a_1, a_2 , a_3 , a_4 , a_5 \})[/tex]
[tex]\qquad P(E) = P(\{a_1, a_2 , a_3 , a_4 \} \cup \{a_5\})[/tex]
[tex]\qquad P(E) = P(\{a_1, a_2 , a_3 , a_4 \}) + P(\{a_5\})[/tex] (usando a condição [tex]\textcolor{#8b4513}{(iii)}\;[/tex] da definição de função probabilidade)
[tex]\qquad P(E) = p_1 + p_2 + p_3+ p_4 + P(\{a_5\})[/tex] (usando os cálculos anteriores)
[tex]\qquad P(E) = p_1 + p_2 + p_3 + p_4+ p_5[/tex].
A repetição sucessiva desse raciocínio nos garante que, de um modo geral, se [tex]E = \{a_{i_1}, a_{i_2}, \ldots , a_{i_k}\}[/tex] com [tex]\{i_1, i_2, \ldots, i_k\} \subset \{1, 2, \ldots , n\}[/tex] e [tex]i_m \neq i_p[/tex] para [tex]m \neq p[/tex], temos que:
[tex]\qquad \boxed{P(E) = P(\{a_{i_1}\}) + P(\{a_{i_2}\}) + \ldots + P(\{a_{i_k}\})}[/tex],
ou seja, a probabilidade de um evento com mais de um ponto amostral é a soma das probabilidades dos eventos elementares que estão contidos nesse evento.
Consequência desta propriedade: Observe que, neste caso, [tex]\boxed{p_1 + p_2 + \ldots + p_n = 1}[/tex], já que [tex]P(\Omega) = 1[/tex]:
[tex]\qquad P(\Omega) = 1[/tex]
[tex]\qquad P(\{a_1 , a_2, \ldots , a_n\})=1[/tex]
[tex]\qquad P(\{a_1\}) + P(\{a_2\}) + \ldots + P(\{a_n\}) = 1[/tex]
[tex]\qquad \boxed{p_1 + p_2 + \ldots + p_n = 1}[/tex].
Vejamos um exemplo prático para utilização da propriedade 7.
Uma fábrica está fazendo um experimento no qual cinco fibras com diferentes comprimentos são submetidas a um teste para se determinar qual fibra se romperá primeiro. Os dados supostos são os seguintes:
• Os comprimentos das fibras são [tex]1,2,3,4\,[/tex] e [tex]\,5[/tex] centímetros.
• A probabilidade de uma fibra ser a primeira a se romper é proporcional ao comprimento daquela fibra.
Qual a probabilidade de que o comprimento da fibra que se romperá primeiro não seja superior a [tex]3[/tex] centímetros?
Com a propriedade 7, para definirmos uma função probabilidade em um espaço amostral finito só é preciso conhecer a probabilidade dos eventos elementares que compõem esse espaço amostral. E uma classe importante de espaços amostrais finitos para os quais a definição das probabilidades dos eventos elementares é muito simples são os chamados Espaços Amostrais Equiprováveis.
Dizemos que [tex]\Omega[/tex] é um Espaço Amostral Equiprovável se cada evento elementar tem a mesma probabilidade de ocorrer.
Propriedade
(8) Em um espaço amostral equiprovável e com [tex]n[/tex] elementos, a probabilidade a ser atribuída a cada evento elementar é [tex]\dfrac{1}{n}\,.[/tex]
Com efeito, consideremos uma vez mais um experimento aleatório com espaço amostral finito [tex]\Omega=\{a_1 , a_2, \ldots , a_n\}[/tex], cujos eventos elementares são [tex]E_1 = \{a_1\}[/tex], [tex]E_2 = \{a_2\}[/tex], [tex]\ldots[/tex] , [tex]E_n = \{a_n\}[/tex] e suas respectivas probabilidades são [tex]p_1, p_2, \ldots, p_n[/tex].
Se [tex]\Omega[/tex] for equiprovável, então temos [tex]p_1 = p_2 = \ldots = p_n = p[/tex] e, portanto, pela Consequência da propriedade (7), obtemos:
[tex]\qquad p_1 + p_2 + \ldots + p_n = 1[/tex]
[tex]\qquad \underbrace{p+\ldots+p}_{n \text{ parcelas}} = 1[/tex]
[tex]\qquad n \cdot p = 1[/tex]
[tex]\qquad \boxed{p =\dfrac{1}{n}}\,.[/tex]
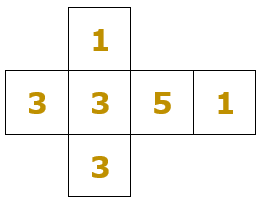
Consideremos um dado que tenha em suas faces dois números [tex]1[/tex], três números [tex]3[/tex] e um número [tex]5[/tex], de acordo com a planificação mostrada na próxima figura.
Supondo que este dado seja balanceado e o lançamento não favoreça qualquer uma das faces, lançado o dado, quais as probabilidades de conseguirmos uma face com [tex]1[/tex]? E [tex]3[/tex]? E [tex]5[/tex]?
Solução:
Podemos definir o espaço amostral do experimento como [tex]\Omega_1=\{f_1=1;f_2=3;f_3=3,f_4=5,f_5=1,f_6=3\}[/tex].
Neste caso, considere os seguintes eventos:
[tex]\qquad A:[/tex] A face obtida é [tex]1[/tex]. Neste caso, [tex]A=\{f_1=1;f_5=1\}[/tex].
[tex]\qquad B:[/tex] A face obtida é [tex]3[/tex]. Neste caso, [tex]B=\{f_2=3;f_3=3,f_6=3\}[/tex].
[tex]\qquad C:[/tex] A face obtida é [tex]5[/tex]. Neste caso, [tex]C=\{f_4=5\}[/tex].
Observe que estamos considerando um dado balanceado, de modo que nenhuma face seja favorecida no lançamento. Assim, [tex]\Omega[/tex] é equiprovável e, portanto:
[tex]\qquad P(\{f_1\})=P(\{f_2\})=P(\{f_3\})=P(\{f_4\})=P(\{f_5\})=P(\{f_6\})=\dfrac{1}{6}\,.[/tex]
Com isso, utilizando a Propriedade (7) obtemos as seguintes probabilidades:
[tex]\qquad \qquad P(A)=\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{2}{6}=\dfrac{1}{3}\\
\qquad \qquad P(B)=\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{3}{6}=\dfrac{1}{2}\\
\qquad \qquad P(C)=\dfrac{1}{6}\,.[/tex]
Perceba, agora, que poderíamos ter descrito o experimento definindo o seu espaço amostral como [tex]\Omega_2=\{1,3,5\}[/tex]. Neste caso, teríamos um espaço amostral com menos eventos elementares, mas ele seria um espaço não equiprovável. Intuitivamente é fácil perceber a não equiprobabilidade, já que, ao jogarmos esse dado, se quisermos prever o resultado é mais razoável arriscar um palpite no número [tex]3[/tex], não é?
Mas com os cálculos feitos comprovamos, de fato, que as probabilidades dos eventos elementares [tex]\{1\}[/tex], [tex]\{3\}[/tex] e [tex]\{5\}[/tex] são distintas:
[tex]\qquad P(\{1\})=\dfrac{1}{3}[/tex] , [tex]P(\{3\})=\dfrac{1}{2}[/tex] e [tex]P(\{5\})=\dfrac{1}{6}[/tex].
Vamos fazer mais um exemplo no qual podemos observar mais uma vez que a definição do espaço amostral de um experimento não é única.
Dois dados comuns não viciados são jogados simultaneamente.
Calcular a probabilidade de que a soma dos números mostrados nas faces voltadas para cima seja [tex]6[/tex].

Solução:
Podemos definir o espaço amostral do experimento a partir da tabela abaixo, na qual aparecem pares ordenados formados por todas as possíveis combinações de resultados dos números mostrados nas duas faces voltadas para cima.
[tex]\begin{array}{|c|c|c|c|c|c|c|}
\hline
\text{Dados}&1&2&3&4&5&6\\
\hline
1&(1,1)&(1,2)&(1,3)&(1,4)&(1,5)&(1,6)\\
\hline
2&(2,1)&(2,2)&(2,3)&(2,4)&(2,5)&(2,6)\\
\hline
3&(3,1)&(3,2)&(3,3)&(3,4)&(3,5)&(3,6)\\
\hline
4&(4,1)&(4,2)&(4,3)&(4,4)&(4,5)&(4,6)\\
\hline
5&(5,1)&(5,2)&(5,3)&(5,4)&(5,5)&(5,6)\\
\hline
6&(6,1)&(6,2)&(6,3)&(6,4)&(6,5)&(6,6)\\
\hline
\end{array}[/tex]
Observamos com a tabela que temos [tex]36[/tex] pares ordenados possíveis de números mostrados nas faces voltadas para cima de cada dado e, assim, temos um primeiro espaço amostral para o experimento:
[tex]\qquad \Omega_3=\{(1,1);(1,2); (1,3); \ldots ;(6,4); (6,5);(6,6)\}[/tex].
Observe que a menor soma possível é [tex]1+1=2[/tex] e, a maior, [tex]6+6=12[/tex].
Como não estamos interessados nos números propriamente ditos que aparecem nas duas faces e sim nas suas somas, também podemos representar os possíveis resultados do experimento utilizando o conjunto dessas somas. Nesse caso, temos um segundo espaço amostral que descreve o experimento, com apenas onze elementos:
[tex]\qquad \Omega_4=\{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}\,.[/tex]
Perceba que utilizando o espaço amostral [tex]\Omega_3[/tex] descrito pela tabela, obtemos facilmente as situações nas quais ocorre a soma [tex]6[/tex].
[tex]\begin{array}{|c|c|c|c|c|c|c|}
\hline
\text{Dados}&1&2&3&4&5&6\\
\hline
1&(1,1)&(1,2)&(1,3)&\text(1,4)&\textcolor{red}{(1,5)}&(1,6)\\
\hline
2&(2,1)&(2,2)&(2,3)&\textcolor{red}{(2,4)}&(2,5)&(2,6)\\
\hline
3&(3,1)&(3,2)&\textcolor{red}{(3,3)}&(3,4)&(3,5)&(3,6)\\
\hline
4&(4,1)&\textcolor{red}{(4,2)}&(4,3)&(4,4)&(4,5)&(4,6)\\
\hline
5&\textcolor{red}{(5,1)}&(5,2)&(5,3)&(5,4)&(5,5)&(5,6)\\
\hline
6&(6,1)&(6,2)&(6,3)&(6,4)&(6,5)&(6,6)\\
\hline
\end{array}[/tex]
Assim, o evento que nos interessa é:
[tex]\qquad \qquad E=\{(1,5);(2,4);(3,3);{(4,2)};(5,1)\} \subset \Omega_3[/tex].
Observe que [tex]\Omega_3[/tex] é um espaço amostral com [tex]36[/tex] elementos e é equiprovável, uma vez que, como os dados são não viciados, nenhuma de suas faces é favorecida no lançamento. Dessa forma, a Propriedade (8) nos garante que a probabilidade a ser atribuída a cada evento elementar de [tex]\Omega_1[/tex] é [tex]\dfrac{1}{36}[/tex] e, portanto, pela Propriedade (7) a probabilidade do evento [tex]E[/tex] é dada por:
[tex]\quad P(E)=P(\{(1,5)\})+P(\{(2,4)\})+P(\{(3,3)\})+P(\{(4,2)\})+P(\{(5,1)\})\\
\quad P(E)=\dfrac{1}{36}+\dfrac{1}{36}+\dfrac{1}{36}+\dfrac{1}{36}+\dfrac{1}{36}\\
\quad \fcolorbox{#6d360f}{#f5d2b8}{$P(E)=\dfrac{5}{36}$}\,.[/tex]
Note que ao tentar fazer o mesmo procedimento utilizando o espaço amostral [tex]\Omega_4[/tex] não conseguimos identificar a quantidade de vezes que cada soma ocorre observando apenas os elementos desse espaço amostral. Temos que recorrer “a tabela que definiu [tex]\Omega_3[/tex].
Mais do que isso, recorrendo à tabela, veja algumas probabilidades associadas aos eventos elementares de [tex]\Omega_4[/tex]:
Soma dois: [tex]P(\{2\})=\dfrac{1}{36};\\
[/tex]
Soma três: [tex]P(\{3\})=\dfrac{2}{36}=\dfrac{1}{18};\\
[/tex]
Soma quatro: [tex]P(\{4\})=\dfrac{3}{36}=\dfrac{1}{12}.\\
[/tex]
Perceberam?
Pois é, [tex]\Omega_4[/tex] não é equiprovável!
Se você chegou até aqui lendo com a devida atenção tudo o que foi exposto pode estar se perguntando:
– Mas, o que aconteceu com o que aprendemos na escola de que a probabilidade é o "número de casos favoráveis sobre o número de casos possíveis"? Por que isso não apareceu até agora?
Boa pergunta!
De fato, em livros de matemática da educação básica, a probabilidade de um evento [tex]A[/tex] ocorrer num experimento aleatório com espaço amostral finito [tex]S[/tex] é inicialmente definida como
[tex]\qquad \qquad \boxed{P(A) = \dfrac{n(A)}{n(S)}}[/tex],
onde [tex]n(A)[/tex] e [tex]n(S)[/tex] indicam, respectivamente, o número de elementos de [tex]A[/tex] (número de resultados favoráveis) e o número de elementos de [tex]S[/tex] (número de resultados possíveis).
Essa formula é historicamente importante, pois foi a maneira com que o matemático Laplace definiu probabilidade, e já era conhecida pelo também matemático Cardano, mas ela só vale em casos muito particulares, bem específicos. Resumindo, ela não se aplica sempre!
Observem que os Exemplos 5 e 6 mostram isso:
► No Exemplo 5, se consideramos [tex]\Omega_2=\{1,3,5\}[/tex], vemos que:
[tex]\qquad \qquad P(\{3\})\ne \dfrac{1}{3}[/tex] e [tex]P(\{5\})\ne\dfrac{1}{3}[/tex].
► No Exemplo 6, se consideramos [tex]\Omega_4=\{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}[/tex], vemos que:
[tex]\qquad \qquad P(\{2\})\ne \dfrac{1}{11}\,[/tex] ; [tex]\,P(\{3\})\ne\dfrac{1}{11}\,[/tex] ; [tex]\,P(\{4\})\ne\dfrac{1}{11}\,[/tex] ; [tex]\,\cdots\, ;\, P(\{12\})\ne\dfrac{1}{11}\,. \\
[/tex]
Entretanto, em particular, quando tratamos com eventos em espaços amostrais finitos e equiprováveis, chegamos a isso como conclusão do que vimos aqui. Observem.
Propriedade
(9) Probabilidade de Laplace
Seja [tex]A[/tex] um evento de um espaço amostral finito e equiprovável [tex]S[/tex]. Então a probabilidade de [tex]A[/tex] é definida por
[tex]\qquad \qquad \boxed{P(A) = \dfrac{n(A)}{n(S)}}[/tex],
onde [tex]n(A)[/tex] e [tex]n(S)[/tex] indicam, respectivamente, o número de elementos de [tex]A[/tex] e o número de elementos de [tex]S[/tex].
Com efeito, seja [tex]A[/tex] um evento de um espaço amostral finito equiprovável [tex]S[/tex]. Suponhamos que [tex]S[/tex] tenha [tex]n[/tex] elementos e que [tex]A[/tex] tenha [tex]m[/tex] elementos.
Pela propriedade (8), sabemos que a probabilidade de cada evento elementar de [tex]S[/tex] é [tex]\dfrac{1}{n}\,.[/tex] Logo:
◊ Se [tex]A[/tex] for um evento com mais de um ponto amostral, a propriedade (7) garante que a probabilidade de [tex]A[/tex] é a soma das probabilidades dos eventos elementares que nele estão contidos, ou seja:
[tex]\qquad P(A)=\underbrace{\dfrac{1}{n}+\dfrac{1}{n}+ \ldots +\dfrac{1}{n}}_{m \text{ parcelas}}\\
\qquad P(A)=m \cdot \dfrac{1}{n}=\dfrac{m}{n}\\
\qquad \boxed{P(A) = \dfrac{n(A)}{n(S)}}\,.[/tex]
◊ Se [tex]A[/tex] for um evento com apenas um ponto amostral, então:
[tex]\qquad P(A)=\dfrac{1}{n}\\
\qquad \boxed{P(A) = \dfrac{n(A)}{n(S)}}\,.[/tex]
Esse tipo de probabilidade é também chamado de Probabilidade Clássica e é o tema central da nossa Sala 2.
Antes de encerrarmos as discussões da Sala 1, vamos resolver mais alguns problemas?
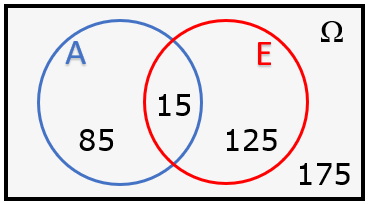
Em um grupo de [tex]400[/tex] alunos de uma universidade, [tex]100[/tex] estudam Administração, [tex]140[/tex] estudam Economia e [tex]15[/tex] estudam Administração e Economia. Se um desses [tex]400[/tex] alunos for escolhido ao acaso, qual a probabilidade de que:
(a) ele estude Administração e Economia?
(b) ele estude apenas Administração?
(c) ele estude apenas Economia?
(d) ele não estude Administração e nem Economia?
(e) ele estude Administração ou Economia?
Os atletas [tex]B[/tex], [tex]F[/tex], [tex]N[/tex], [tex]R[/tex], [tex]S[/tex], [tex]U[/tex] e [tex]W[/tex] vão disputar uma corrida de [tex]200[/tex] metros rasos. A probabilidade de [tex]U[/tex] ganhar a prova é de [tex]\dfrac{1}{7}[/tex]?

Imagem extraída de Freepik
Os algarismos [tex]1,2,3,4,5[/tex] foram escritos em cinco cartões distintos, mas com a mesma forma, mesmo tamanho e mesma cor.
Esses cartões são escolhidos aleatoriamente e sem reposição, e os números que vão aparecendo são escritos da esquerda para a direita, formando um número de cinco algarismos.
Terminada a escolha, qual a probabilidade de que o número escrito tenha sido um número ímpar?

Agora, é com vocês.
Mas se vocês tiverem que definir probabilidades para um espaço amostral, não se esqueçam de verificar com cuidado se esse espaço é equiprovável!
Bom proveito, pessoal!
Equipe COM – OBMEP

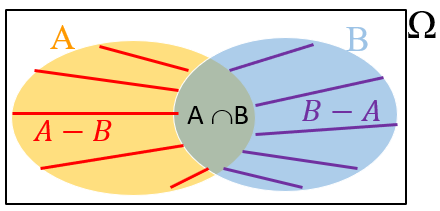
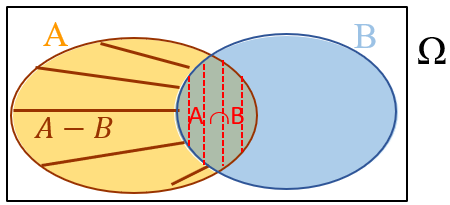
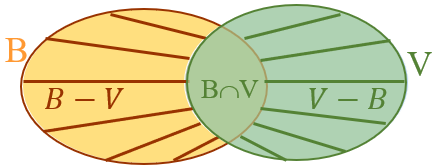
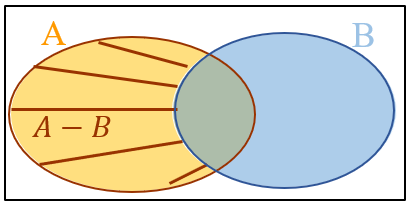 Utilize diagramas e perceba que [tex](A-B) \cup B = A \cup B[/tex] e [tex](A-B) \cap B = \emptyset[/tex].
Utilize diagramas e perceba que [tex](A-B) \cup B = A \cup B[/tex] e [tex](A-B) \cap B = \emptyset[/tex].