✏ Link da Sala para dispositivos da Apple.
na Análise Combinatória
Você já ouviu falar em Análise Combinatória?
Se você já estudou esse assunto, palavras como combinações, arranjos e permutações possivelmente surgiram em sua mente. E isso é natural, já que o estudo da Análise Combinatória, pelo menos em seu estágio inicial, trata da resolução de problemas de Contagem e "combinações, arranjos e permutações" são ferramentas utilizadas para resolver problemas de Contagem.
Mas essas não são as únicas ferramentas que existem na Análise Combinatória. Embora não tão conhecido, o Princípio das Gavetas de Dirichlet (também denominado Princípio das Casas de Pombos), por exemplo, é uma técnica muito eficaz na resolução de determinados problemas de Contagem. (Se você não conhece esse Princípio, você pode encontrar uma Sala de Estudo sobre ele no nosso Blog clicando AQUI.)
Outra lembrança que certamente surge na mente de quem já resolveu problemas de Contagem é a utilização de muitas e muitas fórmulas…
Mas você sabia que não precisamos necessariamente utilizar fórmulas para resolver problemas de Contagem?
Embora muitos exercícios envolvendo Contagem sejam resolvidos utilizando-se alguma das técnicas citadas anteriormente – combinações, arranjos, permutações – nem sempre conseguimos respostas tão facilmente. Mais do que fórmulas, por diversas vezes, a solução de um problema de Contagem exige apenas engenhosidade e a real compreensão da situação apresentada no seu enunciado.
Nesta Sala de Estudos, vamos apresentar um tipo de raciocínio que permite resolver alguns problemas utilizando um pouco de criatividade. Mas, para que você entenda bem os problemas que serão propostos, você vai precisar do Princípio Fundamental da Contagem – PFC. Se você não conhece ou não se lembra desse Princípio, dê uma passadinha nesta Sala do nosso Blog antes de prosseguir. Afinal, o PFC é um dos pilares da Análise Combinatória!
Vamos lá?
Iniciaremos os nossos estudos aprendendo (ou relembrando) o que são anagramas.
Assim, os anagramas de uma dada palavra são as palavras obtidas pelo "embaralhamento" das letras da palavra original (manter as letras mudando ou não a ordem).
- A palavra [tex]PORTA[/tex], por exemplo, possui vários anagramas que fazem sentido, veja alguns:
- [tex]PARTO[/tex]
- [tex]TRAPO[/tex]
- [tex]RAPTO[/tex]
- [tex]TOPAR[/tex]
- [tex]OPTAR[/tex]
- [tex]PRATO[/tex]
- [tex]TROPA[/tex]
- [tex]PTORA[/tex]
- [tex]OARPT[/tex]
- [tex]TORAP[/tex]
Há também anagramas que não fazem sentido, por exemplo:
► Exibimos acima alguns anagramas da palavra [tex]PORTA \, [/tex]. E se quiséssemos saber quantos anagramas essa palavra possui?
-
A ideia de “embaralhar” as letras é a mesma que a de permutá-las; portanto, a palavra [tex]PORTA[/tex] possui:
- Observe, inicialmente, o número de escolhas para cada posição das letras, lembrando que as letras não se repetem.
- Assim, pelo Princípio Fundamental da Contagem, o número de modos distintos de embaralharmos as letras da palavra [tex]PORTA \, [/tex] é dado por [tex] \, \fcolorbox{#589386}{#ddebe8}{$\textcolor{blue}{5}\times \textcolor{blue}{4}\times \textcolor{blue}{3}\times \textcolor{blue}{2}\times \textcolor{blue}{1}=120$} \, .[/tex]
[tex]\qquad \qquad 5!=5\times 4\times 3\times 2\times 1=120[/tex] anagramas.
Vamos visualizar essa conta?
[tex]\begin{array}{c c c c c}
\textcolor{blue}{5}\text{ escolhas}&\textcolor{blue}{4}\text{ escolhas}&\textcolor{blue}{3}\text{ escolhas}&\textcolor{blue}{2}\text{ escolhas}&\textcolor{blue}{1}\text{ escolha}\\
\overline{\text{primeira letra}}&\overline{\text{segunda letra}}&\overline{\text{terceira letra}}& \overline{\text{quarta letra}}& \overline{\text{quinta letra}}
\end{array}[/tex]
Agora, vamos ver dois exemplos motivadores do raciocínio que iremos explorar.
► Vamos calcular em quantos anagramas da palavra [tex]PORTA[/tex] as vogais aparecem em ordem alfabética, ou seja, vamos determinar em quantos anagramas a letra [tex]A[/tex] aparece antes da letra [tex]O[/tex]. Como podemos resolver esse problema?
Você deve ficar atento ao fato de que as vogais não precisam estar juntas. A palavra [tex]PARTO[/tex] é um dos anagramas que satisfazem às condições do problema. E [tex]AOTRP[/tex] também o é.
Uma possível solução para o problema é a seguinte:
Qualquer anagrama da palavra [tex]PORTA[/tex] está em um dos dois grupos:
- Palavras em que o [tex]A[/tex] aparece antes do [tex]O.[/tex]
- Palavras em que o [tex]O[/tex] aparece antes do [tex]A.[/tex]
Note que os dois grupos possuem a mesma quantidade de anagramas (trocando o [tex]A[/tex] pelo [tex]O[/tex] temos um anagrama de cada grupo).
Logo, a resposta do problema é [tex] \, \fcolorbox{#589386}{#ddebe8}{$\dfrac{5!}{2}=60$}:[/tex] metade do total de todos os anagramas.
► Troquemos de palavra. Se a palavra for [tex]ALUNO[/tex], quantos são os anagramas em que as vogais estão em ordem alfabética?
-
Neste exemplo, observamos que os possíveis anagramas podem ser agrupados em seis grupos:
- Palavras em que primeiro temos a letra [tex]A[/tex], depois [tex]O[/tex] e depois [tex]U.[/tex]
- Palavras em que primeiro temos a letra [tex]A[/tex], depois [tex]U[/tex] e depois [tex]O.[/tex]
- Palavras em que primeiro temos a letra [tex]O[/tex], depois [tex]A[/tex] e depois [tex]U.[/tex]
- Palavras em que primeiro temos a letra [tex]O[/tex], depois [tex]U[/tex] e depois [tex]A.[/tex]
- Palavras em que primeiro temos a letra [tex]U[/tex], depois [tex]A[/tex] e depois [tex]O.[/tex]
- Palavras em que primeiro temos a letra [tex]U[/tex], depois [tex]O[/tex] e depois [tex]A.[/tex]
Novamente, todos esses grupos contêm a mesma quantidade de anagramas.
Perceba que queremos apenas o primeiro grupo, pois nele as vogais estão em ordem alfabética; como a palavra [tex]ALUNO[/tex] possui [tex]5![/tex] anagramas a resposta deste problema é [tex] \, \fcolorbox{#589386}{#ddebe8}{$\dfrac{5!}{6}=20$} \, [/tex], ou seja, um sexto do total dos anagramas da palavra em questão.
Nos dois exemplos, é importante perceber que das [tex]120[/tex] permutações de cinco elementos escolhemos apenas aquelas em que as vogais não permutaram entre si. Assim, os grupos em que dividimos os anagramas, nos dois exemplos, “surgiram” da respectiva quantidade de permutações das vogais de cada palavra: [tex]2=2![/tex], na palavra porta, e [tex]6=3![/tex], na palavra aluno.
Dessa forma, a resposta poderia ser calculada por [tex] \, \boxed{\dfrac{5!}{2!}} \, [/tex], no caso da palavra porta , e [tex] \, \boxed{\dfrac{5!}{3!}} \, [/tex], no exemplo da palavra aluno.
Nas duas situações, a divisão por [tex]2![/tex] e [tex]3! \, [/tex], respectivamente, pode ser entendida como uma correção que fazemos no cálculo dos anagramas ([tex]5![/tex]), já que as vogais de cada palavra não podem trocar de lugar entre si.
Vamos fazer mais um exemplo para ver se está entendida a estratégia?
Que tal você tentar resolver este problema?
Depois, clique no botão abaixo para ver a solução.
Passando a limpo…
– Ignoramos a princípio as restrições de cada problema e iniciamos contando casos a mais.
– Em um segundo momento, desconsideramos os casos que não nos interessavam e que foram indevidamente contados.
E como isso foi feito?
✐ Para contar sem restrições, nada mais útil do que utilizar o PFC: Princípio Fundamental da Contagem.
✄ Para descontar o que foi indevidamente contado, utilizamos divisões.
Assim, acabamos de descobrir mais uma utilidade da divisão:
eliminar casos indevidamente contados em uma permutação.
Precisam de mais problemas?
O senhor Bruno realiza cinco atividades diárias durante as manhãs da semana. São elas:
- Levar a filha à escola;
- Tomar café da manhã:
- Comprar o Jornal;
- Fazer exercícios físicos;
- Buscar a filha na escola.
De quantas maneiras diferentes o senhor Bruno poderia fazer essas atividades?
E se as atividades do senhor Bruno fossem:
- Levar a filha à escola;
- Tomar café da manhã:
- Comprar o Jornal;
- Fazer exercícios físicos;
- Buscar a filha na escola;
- Ler o Jornal;
de quantas maneiras ele poderia executá-las?

Na imagem acima temos doze crianças – sete meninos e cinco meninas- e todos com alturas diferentes.
De quantas maneiras podemos formar uma fila, de forma que os meninos entre si e as meninas entre si estejam em ordem crescente de altura?

Martín teve a ideia de convidar todos os sete novos amigos para um churrasco. Para isso, é necessário ir até à casa de cada um deles. De quantas maneiras isso pode ser feito se a primeira casa visitada deve ser a da Magali e, para que não haja brigas, antes de passar na casa do Cebolinha e do Cascão, Martín deve passar na casa da Mônica?
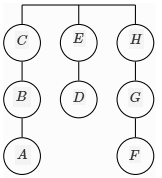
Em um torneio de tiro, oito alvos são dispostos em três correntes penduradas, como mostra a figura abaixo.
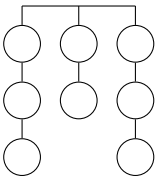
Os primeiros alvos de cada corrente estão presos a um suporte e os outros estão presos aos respectivos alvos imediatamente acima.
Para ganhar a competição todos os oito alvos devem ser atingidos. Assim, se um competidor acertar um alvo sem ter atirado no(s) que está(ão) abaixo, este(s) cairá(ão) e o competidor não ganhará a pontuação relativa aos alvos perdidos.
Para obter a pontuação máxima do torneio, de quantas maneiras diferentes cada competidor pode acertar os oito alvos?
Os próximos problemas são para vocês…
Problema 6
Quantos são os anagramas da palavra [tex]UNIVERSO[/tex] em que as vogais aparecem em ordem alfabética?
Problema 7
Vamos formar sequências com todos os números naturais [tex]1, \, 2, \, \cdots , \, 10[/tex] de modo que o [tex]5[/tex] esteja situado à direita do [tex]2[/tex] e à esquerda do [tex]3[/tex], embora não necessariamente em lugares consecutivos.
Quantas sequências obteremos?
Um dos desenhos mais famosos e engraçados de competição é o "CORRIDA MALUCA". Nele os carros dos onze competidores são numerados de 00 a 10.

Na próxima corrida, os competidores serão colocados em fila, de maneira que os números pares fiquem em ordem decrescente e os ímpares em ordem crescente.
De quantas maneiras diferentes isso pode ser feito?
Um dos competidores da "CORRIDA MALUCA" é o Dick Vigarista (carro 00).

Como o próprio nome indica, ele sempre tenta trapacear durante as corridas. Por esse motivo, na próxima corrida, ele deverá largar na última posição.
De quantas maneiras poderá ser montada a largada, respeitando a ordem estabelecida no problema anterior?
Bom trabalho, pessoal!
Equipe COM – OBMEP
Abril de 2018.
[1] Pais & Filhos (Último acesso em 14/06/20)
[2] Maurição (Último acesso em 14/06/20)
[3] TN (Último acesso em 14/06/20)
[4] Mercado Livre (Último acesso em 14/06/20)