O que é calcular um volume?
Intuitivamente falando, o volume de um objeto espacial, um sólido, é a “quantidade de espaço que esse objeto ocupa”.
Para indicar numericamente essa “quantidade de espaço”, devemos medir esse espaço, ou seja, devemos compará-lo com o espaço ocupado por um objeto espacial tomado como padrão. O resultado dessa comparação é um número que nos diz quantas vezes a unidade de medida utilizada cabe no espaço que está sendo medido.
Parece que vocês já ouviram uma história parecida; mas com outros personagens, não é?
Mas vamos continuar e responder a pergunta feita: O que é calcular um volume?
– “Calcular o volume de um objeto espacial” é determinar a medida do volume desse objeto.
Assim, para calcular o volume de uma figura espacial, precisamos de uma unidade de medida igualmente espacial.
Neste caso, em vez de um quadrado de lado 1, como no cálculo de áreas, a unidade de medida convencional é o espaço ocupado por um cubo unitário, isto é, um cubo cujas arestas medem 1 unidade de medida de comprimento.

Calcular o volume de uma figura espacial, portanto, é calcular quantos cubos unitários cabem na figura espacial em questão.
Vale lembrar que o metro cúbico é a unidade padrão das medidas de volume definido pelo SI, Sistema Internacional de Medidas. Um metro cúbico ( 1 m3) corresponde ao espaço ocupado por um cubo cujas arestas medem 1 metro de comprimento.

Para medir volumes maiores ou menores usamos, respectivamente, os seus múltiplos (decâmetro cúbico, hectômetro cúbico e quilômetro cúbico) e submúltiplos (decímetro cúbico, centímetro cúbico e milímetro cúbico). Para converter qualquer uma delas em outra, podemos utilizar o esqueminha abaixo.
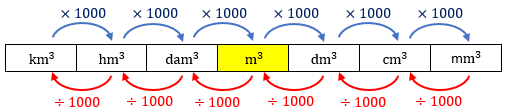
Estes conceitos iniciais são revisados de forma muito precisa no vídeo abaixo.
Um vídeo para ajudar. . .
Para assistir, é só clicar na setinha.
Paralelepípedo retângulo e seu volume
Vídeo extraído do Portal da Matemática OBMEP
Pelo exposto no vídeo, o volume de um paralelepípedo como o da figura abaixo é dado pelo produto das medidas do comprimento c, da largura l e da altura h, ou seja:
[tex]\qquad \fcolorbox{black}{#dee9f2}{$\text{Volume}_\text{paralelepípedo }=c \times l \times h$}\,.[/tex]
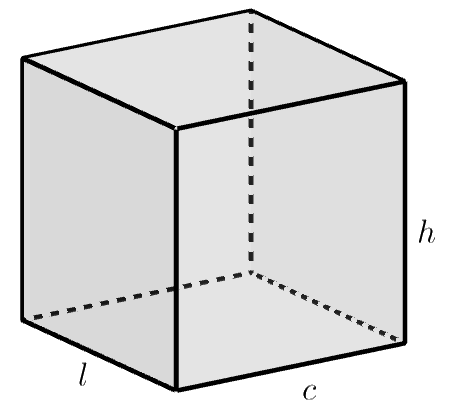
Como a área da base do paralelepípedo da figura é dada por
[tex]\qquad A_{base}=c\times l[/tex],
podemos escrever este volume como
[tex]\qquad \fcolorbox{black}{#dee9f2}{$V=A_{base}\times h$}\,.[/tex]
O mesmo vale para os prismas em geral, isto é, para todos os sólidos definidos por duas bases poligonais iguais e faces laterais retangulares, como na figura abaixo.
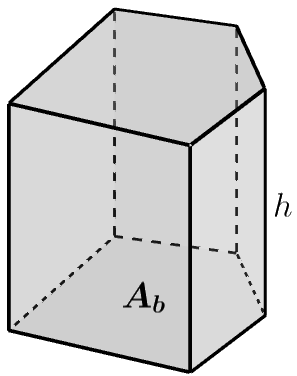
Portanto, de forma geral, o volume Vp de um prisma reto é dado pelo produto entre a área da sua base e a sua altura:
[tex]\qquad \fcolorbox{black}{#dee9f2}{$V_p=A_{base}\times altura$}\,.[/tex]
Vejam que resultado surpreendente; não importa se um prisma é regular ou não, se ele é um prisma reto ou oblíquo: o seu volume será SEMPRE determinado pelo produto entre a área da sua base e a sua altura!
O único cuidado com o cálculo do volume de um prisma é observar atentamente o formato do polígono que define a sua base. Por exemplo, na figura abaixo vemos a fórmula explícita para o cálculo dos volumes de dois prismas: um prisma trapezoidal e um prisma retangular (paralelepípedo).
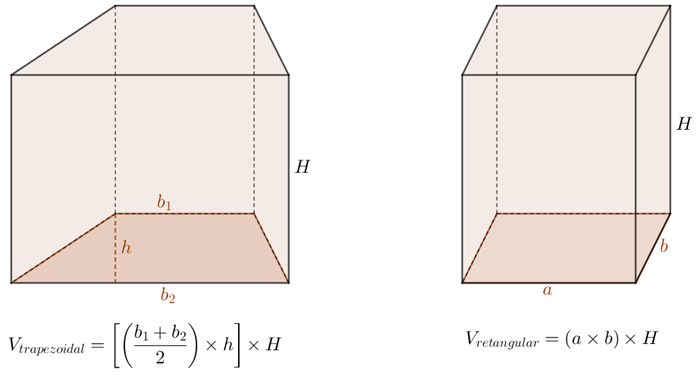
Você já deve ter percebido que muitos objetos do nosso cotidiano podem ser considerados exemplos de prismas; mas encontramos frequentemente outro tipo de sólido: os cilindros. É só observar a próxima imagem ou pensar nas várias latas e latinhas que vemos diariamente!
 Fonte: Projeto SEEDUC. Cecierj. Prismas e Cilindros
Fonte: Projeto SEEDUC. Cecierj. Prismas e Cilindros
Mas e o volume dos cilindros?
Nas nossas próximas atividades, vamos explorar uma enxurrada de volumes.
É só clicar nos botões das Atividades 16 e 17 e participar da exploração!
Particularmente, vocês vão encontrar o volume dos cilindros na Atividade 16.
O foco das nossas últimas atividades é um bem muito precioso e essencial à vida: a água!
Para participar das atividades, clique na imagem abaixo.
 Imagem adaptada de iStock (Acesso em 12/05/23)
Imagem adaptada de iStock (Acesso em 12/05/23)
Equipe COM – OBMEP
