No nosso dia a dia estamos acostumados a lidar com medidas numéricas e com o ato de medir, não é?
O vídeo a seguir ajuda a ilustrar o que estamos falando; assim, cliquem na setinha e acompanhem com atenção as várias situações cotidianas que irão aparecer.
Um vídeo para começar. . .
Novo Telecurso – Ensino Fundamental – Matemática
O que é medir?
Mas o que significa medir?
Em qualquer das situações apresentadas no vídeo, podemos notar que, de maneira prática, medir é comparar “algo” com um referencial. Esse referencial é o que chamamos unidade de medida e o que vai ser medido é o que chamamos de grandeza.
De maneira um pouco mais precisa, mas ainda prática, medir uma grandeza significa verificar “quantas vezes” uma unidade (uma grandeza de mesma espécie tomada como referência) cabe dentro desta. Então, o valor numérico da medida corresponde a essa quantidade de vezes que a unidade cabe na grandeza que está sendo medida. (Entendemos aqui o termo “quantas vezes” em um sentido amplo, uma vez que podemos nos referir a uma quantidade não inteira.)
– Largura, peso, distância, velocidade, área, volume, entre outros, são exemplos de grandezas.
Em Matemática, uma grandeza também pode ser considerada como “algo que pode ser medido”. Mas tanto na Matemática como na prática devemos ter três coisas em mente ao fazermos medidas:
- Não confundir grandeza com o objeto: o que vai ser medido é a grandeza e não o objeto em si.
Por exemplo, é o comprimento da régua mostrada na figura abaixo que mede pouco mais de 10 cm e não a régua (afinal a régua também tem largura, não é?).
Imagem adaptada de Freepik (Acesso em 12/05/23) - Para cada grandeza existe uma unidade que é o padrão escolhido para medi-la. Sem a unidade correspondente, as medidas podem levar a erros.
Observe a figura a seguir e perceba a confusão que seria se não especificássemos as unidades utilizadas nas medições indicadas. Por exemplo, o quadrinho seria maior do que a mesa na qual ele está apoiado e as gavetas nem caberiam sob a mesa!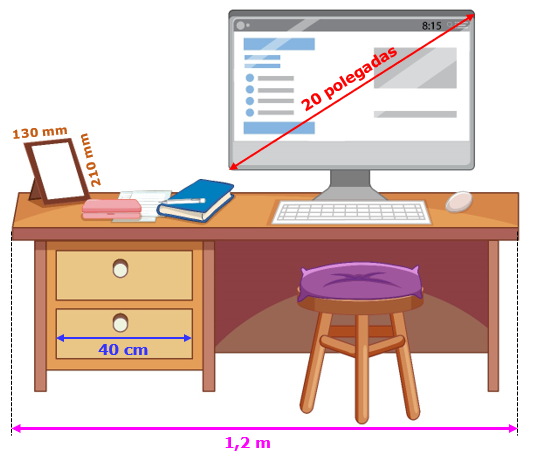
Imagem adaptada de Freepik (Acesso em 12/05/23) - Medir é uma atividade que envolve a comparação de grandezas. No entanto, ao verificar quantas vezes uma das grandezas “cabe” na outra, essas grandezas devem ser da mesma natureza (comprimento com comprimento; área com área; volume com volume etc.).
Por exemplo, não dá para medir o comprimento do pescoço de uma girafa com o volume de água contido em baldes.
Imagens adaptadas de Freepik (Acesso em 12/05/23)
Sabemos que comprimento, peso, distância, velocidade, aceleração, temperatura, massa são exemplos de grandezas. Essas grandezas citadas, assim como a maioria das que medimos diariamente, podem ser classificadas como escalares ou vetoriais. O que diferencia esses dois tipos são as diferentes informações utilizadas para que essas grandezas possam ser definidas. As grandezas escalares podem ser definidas completamente se utilizarmos apenas um número e uma unidade de medida. Já as grandezas vetoriais precisam de mais informações para serem definidas; além do seu valor numérico e da unidade de medida, são necessárias mais duas informações: direção e sentido.
- Grandezas escalares são grandezas que podem ser escritas na forma de um número seguido de uma unidade de medida. Assim, uma grandeza desse tipo fica completamente determinada se soubermos o seu valor (também chamado de módulo) e a forma como ela é medida.
São exemplos de grandezas escalares o comprimento, o tempo, a temperatura e a massa. (Cuidado: balanças medem as massas dos objetos, não o peso deles.) - Grandezas vetoriais são grandezas que NÃO podem ser escritas utilizando-se apenas um número seguido de uma unidade de medida. Para que uma grandeza desse tipo fique completamente determinada ela precisa ser expressa por um número (módulo), uma direção, um sentido e uma unidade de medida.
Vejam alguns exemplos de grandezas vetoriais: posição, deslocamento, velocidade, aceleração e força.
Em poucas palavras:
Podemos explorar a diferença desses dois tipos de grandezas com alguns exemplos práticos.
Quando uma mãe informa ao médico que a temperatura de seu filho está 38,5 graus centígrados, o médico não precisa perguntar qual é a direção, ou seja, se a temperatura informada está 38,5 graus centígrados à direita ou à esquerda, não é?
Apenas com a informação 38,5 graus centígrados, o médico irá dizer à mãe que seu filho está com febre.
Imagem adaptada de Freepik (Acesso em 12/05/23)
Portanto, a temperatura é uma grandeza escalar.
Assim, ao informar que são necessários 200 gramas de fubá para fazer um bolo, a receita não informa que são 200 gramas para cima, ou da direita para a esquerda…
Imagem adaptada de Freepik (Acesso em 12/05/23)
Assim, a temperatura é uma grandeza escalar.
Se soubermos apenas que um barco está se movendo a 80 km/h não podemos prever seu destino; para que isso aconteça, é necessário conhecermos a direção e o sentido da velocidade!
Imagem adaptada de Freepik (Acesso em 12/05/23)
A direção nos informa a reta em que o movimento acontece: é na vertical? é na horizontal? é inclinado?
Definida a direção, precisamos ainda saber o sentido do movimento: é para frente? é para trás? é do norte para o sul? é para a esquerda?
Dessa forma, se tivermos a informação de que o barco está navegando a 80 km/h, na direção horizontal e da esquerda para a direita, podemos representar a velocidade pela flechinha alaranjada da figura a seguir e termos uma ideia do movimento desse barco.
Imagem adaptada de Freepik (Acesso em 12/05/23)
Logo, a velocidade é uma grandeza vetorial.
Quando dizemos que o volume daquele galão de água é 20 litros, não precisamos complementar a informação dizendo 20 litros à esquerda ou de baixo para cima!
Imagem adaptada de Freepik (Acesso em 12/05/23)
Então, o volume é uma grandeza escalar.
Alguém deu a informação de que na competição de cabo de guerra ilustrada abaixo a corda não se mexeu, pois cada criança aplicou uma força de 17 N e, com isso, o somatório de forças de cada lado foi igual!
Observe que se tivéssemos apenas a informação de que na competição foi aplicada uma força de 51 N na corda, nada poderíamos concluir. O que nos fez concluir que a corda não se mexeu, foi a direção e o sentido de aplicação das forças: as forças foram aplicadas em sentidos opostos e tinham a mesma intensidade; consequentemente elas se anularam.
Imagem extraída de Freepik (Acesso em 12/05/23)
Portanto, a força é uma grandeza vetorial.
Antes de iniciarmos nossas atividades de medição, não poderíamos deixar de mencionar um terceiro tipo de grandeza: as Grandezas tensoriais, que fogem completamente ao espírito desta breve introdução. Só para exemplificar, o Momento de Inércia de Área é uma grandeza tensorial usada no estudo de deformação aplicado em projetos de estruturas. É uma grandeza associada à inércia de rotação de um corpo massivo.
Agora, vamos para as nossas atividades.
Boa diversão, pessoal!
Nas atividades que vamos apresentar, exploraremos, particularmente, duas grandezas escalares geométricas: Área e Volume.
Isso significa que nas nossas atividades iremos trabalhar com dois tipos de Geometria: a Geometria Plana e a Geometria Espacial. Assim, os nossos objetos de estudo poderão ter duas ou três dimensões.
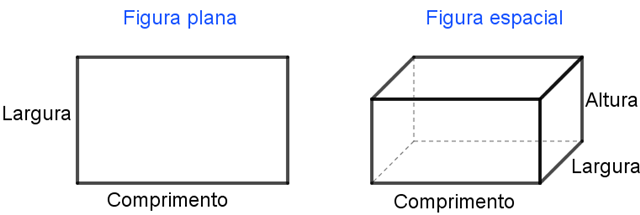
- Os objetos com duas dimensões (comprimento e largura), como uma folha de papel, são os estudados na Geometria Plana e, de modo geral, são chamados de “objetos planos” ou “figuras planas” ou “superfícies planas”.
- Os objetos com três dimensões (comprimento, largura e altura), como uma caixa, são os estudados na Geometria Espacial e são chamados de “objetos espaciais” ou “figuras espaciais” ou “objetos sólidos”.
Dessa forma, para facilitar o entendimento e a prática das atividades relativas às duas grandezas escalares que trabalharemos, dividiremos a nossa discussão em duas Salas, praticamente independentes. Mas sugerimos que essas Salas sejam acessadas na ordem na qual estão apresentadas. No canto inferior direito da página de cada uma delas, vocês encontrarão um link para voltarem para esta Sala Central e, se for necessário, fazer uma nova escolha. As duas Salas abrirão em janelas diferentes do navegador de vocês.
Equipe COM – OBMEP
Junho de 2023.
[1] BIANCHINI, Edwaldo; MIANI, Marcos. Construindo conhecimentos em Matemática, 5ª e 6ª séries. 1ª Edição. São Paulo: Moderna, 2000.
[2] DOLCE, Edwaldo; POMPEO, Marcos. Fundamentos de matemática elementar, volumes 9 e 10. 2ª Edição. São Paulo: Atual, 1978.
[3] IMENES, Luiz Márcio; LELLIS, Marcelo. Matemática paratodos, 5ª e 6ª séries. 1ª Edição. São Paulo: Scipione, 2002.
[4] MOISE, Edwin E.; DOWNS Jr, Floyd L. Geometría Moderna. Primera edición en español. Massachusetts, EE.UU.: Adddison-Wesley, 1966.
[5] Desmos Classroom (Último acesso em 03/03/23)
[6] E haja unidades de medida! – Clubes de Matemática da OBMEP.