Funções
Funções invertíveis (1)
Considere as funções [tex]f[/tex] e [tex]g[/tex] de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex] dadas por [tex]f(x)=x-1 \, [/tex] e [tex] \, g(x)=x+1[/tex]. Observe que:
[tex]\qquad \left( g\circ f\right)=g\left(f(x)\right)[/tex]
[tex]\qquad \qquad \quad \, =g\left(x-1 \right)[/tex]
[tex]\qquad \qquad \quad \, =\left(x-1 \right)+1[/tex]
[tex]\qquad \qquad \quad \, =x[/tex].
Considere agora que [tex]f[/tex] e [tex]g[/tex] são as funções definidas por [tex]g(x)=x ^ 3 +6 \, [/tex] e [tex] \, f(x)=\sqrt[3] {x-6} [/tex] e observe que, para valores reais de [tex]x[/tex]:
[tex]\qquad \left( g\circ f\right)=g\left(f(x)\right)[/tex]
[tex]\qquad \qquad \quad \, =g\left(\sqrt[3] {x-6} \right)[/tex]
[tex]\qquad \qquad \quad \, =\left(\sqrt[3] {x-6} \right)^3+6[/tex]
[tex]\qquad \qquad \quad \, =\left(x-6 \right)+6[/tex]
[tex]\qquad \qquad \quad \, =x[/tex].
Perceba que nas duas situações parece que a função [tex]g[/tex] “desmanchou” o que a [tex]f[/tex] fez:
| Situação 1:
[tex]x \quad \stackrel{\color{#800000}f}{\longrightarrow} \quad x-1 \quad \stackrel{\color{#800000}g}{\longrightarrow} \quad x[/tex] |
Situação 2:
[tex]x \quad \stackrel{\color{#800000}f}{\longrightarrow} \quad \sqrt[3] {x-6} \quad \stackrel{\color{#800000}g}{\longrightarrow} \quad x[/tex] |
De maneira informal, o que vamos tentar fazer agora é responder à seguinte pergunta: dada uma função [tex]f[/tex], em que condições podemos determinar uma função que desfaz a ação executada pela [tex]f[/tex]?
Vamos inicialmente formalizar o que significa “uma função que desfaz a ação executada por uma dada função”; para isso, observe a ilustração abaixo.
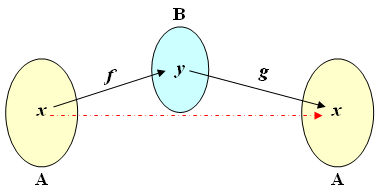
Dada uma função [tex]f: \, A \rightarrow \, B[/tex], para desfazermos a ação de [tex]f[/tex], precisamos produzir uma função [tex]g: \, B \rightarrow \, A[/tex] tal que
[tex]\qquad \left( g\circ f\right)(x)=g\left(f(x)\right)=g\left(y\right)=x [/tex],
ou seja, precisamos produzir uma função [tex]g: \, B \rightarrow \, A[/tex] tal que
[tex]\qquad\left( g\circ f\right)(x)=x [/tex].
Uma função [tex]f[/tex] que tenha o comportamento acima descrito é dita uma função com inversa à esquerda e qualquer função que desfaça a ação de [tex]f[/tex] será dita uma inversa à esquerda para[tex]f[/tex], conforme definição abaixo.
Dizemos que [tex]f[/tex] é uma função com inversa à esquerda se existir uma função [tex]g[/tex] de [tex]B[/tex] em [tex]A[/tex] tal que [tex]\left( g\circ f\right)(x)=x [/tex], para todo [tex]x \in A[/tex].
Neste caso, a função [tex]g[/tex] é dita uma inversa à esquerda para [tex]f[/tex].
Essa é a forma mais conhecida de se desfazer a ação de uma função e, conforme mostrado no texto anexado, para que [tex]f[/tex] tenha inversa à esquerda basta que [tex]f[/tex] seja injetora. No texto, é mostrado mais do que uma condição suficiente, é demonstrado que:
✐ Uma função [tex]f: A \rightarrow B [/tex] tem inversa à esquerda se, e somente se, [tex]f[/tex] for injetora.
De maneira análoga, podemos definir funções com inversas à direita.
Dizemos que [tex]f[/tex] é uma função com inversa à direita se existir uma função [tex]g[/tex] de [tex]B[/tex] em [tex]A[/tex] tal que [tex]\left( f\circ g\right)(x)=x [/tex], para todo [tex]x \in B[/tex].
Neste caso, a função [tex]g[/tex] é dita uma inversa à direita para [tex]f[/tex].
No texto anexado, também será demonstrado que:
✐ Uma função [tex]f: A \rightarrow B [/tex] tem inversa à direita se, e somente se, [tex]f[/tex] for sobrejetora.
Como sabemos que existem funções que são simultaneamente injetoras e sobrejetoras – as bijeções – existem funções que possuem inversas à esquerda e à direita. Neste caso, a função em questão é dita invertível.
Dizemos que [tex]f[/tex] é uma função invertível se existir uma função [tex]g[/tex] de [tex]B[/tex] em [tex]A[/tex] tal que:
[tex]\qquad \left( g\circ f\right)(x)=x [/tex], para todo [tex]x \in A[/tex];
[tex]\qquad \left( f\circ g\right)(x)=x [/tex], para todo [tex]x \in B[/tex].
Neste caso, é possível provar que a função [tex]g[/tex] é única; então ela é dita a inversa de [tex]f[/tex] e é denotada por [tex]f^{-1}[/tex].
Neste primeiro momento, recomendamos que você entenda direitinho as definições e as demonstrações dos resultados apresentados acima, sem a preocupação de como calcular as tais inversas. No próximo domingo, liberaremos o último módulo do curso (ufa…) e nele disponibilizaremos material suficiente para vocês treinarem as continhas.
Antes de encerrarmos esta pequena apresentação, vamos definir uma função que permitirá escrevermos a definição de função invertível de uma maneira ligeiramente diferente.
Chamamos de função identidade do conjunto [tex]A[/tex] a função denotada por [tex]id_A[/tex] e assim definida:
[tex]\qquad id_A: A \rightarrow A [/tex]
[tex]\qquad \qquad id_A(x)=x [/tex].
Veja a nova definição de função invertível.
Dizemos que [tex]f[/tex] é uma função invertível se existir uma função [tex]g: B \rightarrow A [/tex] tal que:
[tex]\qquad g\circ f=id_A[/tex];
[tex]\qquad f\circ g=id_B[/tex].
Dessa forma, se [tex]f^{-1}[/tex] for a inversa da função [tex]f: \, A \rightarrow B[/tex], então temos duas igualdades de funções:
[tex]\qquad f^{-1}\circ f=id_A[/tex];
[tex]\qquad f\circ f^{-1}=id_B[/tex].
A propósito: quando duas funções são iguais?
Um texto para formalizar…
Para ajudar no entendimento dos conceitos aqui apresentados, incluímos mais algumas páginas no material do professor Elon.
Para copiar o material, clique no botão abaixo.
Bons estudos!
Equipe COM – OBMEP
