Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
A figura a seguir representa um Tangram (quebra-cabeça chinês formado por cinco triângulos, um paralelogramo e um quadrado) desenhado em uma malha quadriculada.
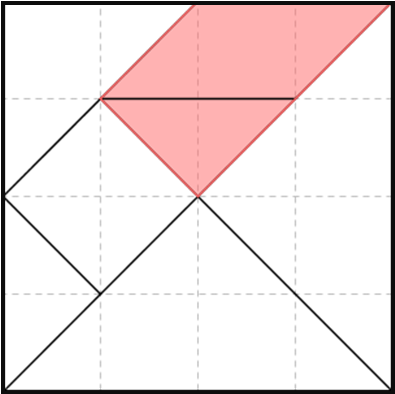
Determine a fração correspondente à área sombreada.
Solução 1
Suponhamos que os quadradinhos que compõem a malha na qual o Tangram foi desenhado tenham lados medindo uma unidade de comprimento. Assim o quadrado externo terá área [tex]A=16[/tex].
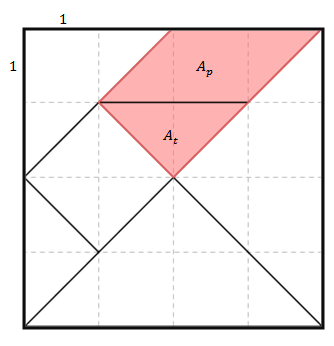
Por outro lado, observe que a área sombreada, [tex]A_s[/tex], corresponde à soma da área de um triângulo, [tex]A_t[/tex], com a área de um paralelogramo, [tex]A_p[/tex], então:
[tex]\qquad \qquad A_s=A_t+A_p=\dfrac{2 \times 1}{2}+(2 \times 1)=3[/tex].
Portanto, a fração do Tangram correspondente à área sombreada será a razão entre a parte e o todo, ou seja, a razão entre [tex]A_s[/tex] e [tex]A[/tex]:
[tex]\qquad \qquad \dfrac{A_s}{A}=\boxed{\dfrac{3}{16}}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
A fração correspondente à área sombreada é [tex]3/16[/tex].
Se dividirmos o quadrado maior em triângulos pequenos, que serão a metade dos quadradinhos menores da figura, poderemos contar [tex]32[/tex] triângulos pequenos, e se formos contar a quantidade de triângulos pequenos na área sombreada, contaremos [tex]6[/tex] deles.
Portanto a fração correspondente à área sombreada é [tex]6/32=3/16[/tex].
Solução elaborada pelo Clube Os Aritméticos.
Complicando o probleminha…
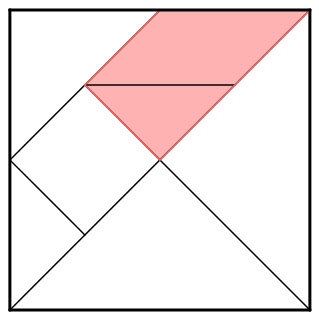
Como resolveríamos este mesmo problema, se o Tangram não tivesse sido desenhado em uma malha quadriculada?
Determine a fração correspondente à área sombreada.

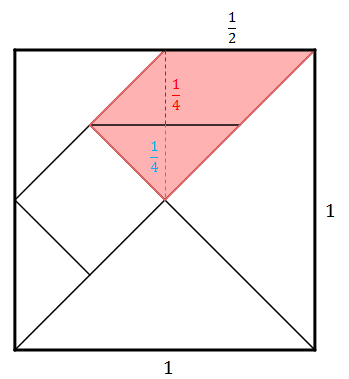 Por outro lado, observe que a região sombreada é composta por um triângulo e por um paralelogramo; dessa forma, a área da região sombreada, [tex]A_s[/tex], é a soma das áreas desse triângulo, [tex]A_t[/tex], e desse paralelogramo, [tex]A_p[/tex], e, portanto:
Por outro lado, observe que a região sombreada é composta por um triângulo e por um paralelogramo; dessa forma, a área da região sombreada, [tex]A_s[/tex], é a soma das áreas desse triângulo, [tex]A_t[/tex], e desse paralelogramo, [tex]A_p[/tex], e, portanto: