✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 2º ano do E. M.)
Jorge esqueceu o último algarismo da senha numérica do computador do seu escritório, mas lembra-se de que não era o zero.
Ele possui no máximo três tentativas para acertar a senha correta. Caso não acerte, o computador será bloqueado.
Se testar as opções aleatoriamente, qual é a chance de Jorge conseguir acertar a senha sem bloquear o computador?

AJUDA
✐ Sabemos que um evento [tex]E[/tex] pode ocorrer ou não. Se o evento [tex]E[/tex] for relativo a um espaço amostral [tex]\, \Omega[/tex], o evento associado à não ocorrência de [tex]E[/tex] é denominado o complementar de [tex]E[/tex] com relação a [tex]\, \Omega[/tex] e é denotado por [tex]\overline{E}[/tex].
- Logo, [tex]\overline{E}[/tex] ocorre se, e somente se, [tex]E[/tex] não ocorrer.
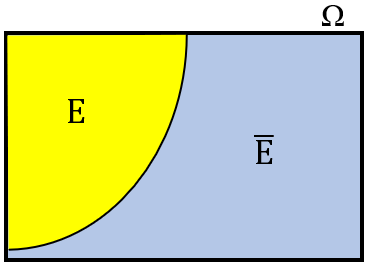
Dessa forma, se [tex]P[/tex] for a probabilidade de que o evento [tex]E[/tex] ocorra (sucesso) e [tex]Q[/tex] for a probabilidade de que [tex]E[/tex] não ocorra (insucesso), então [tex]Q[/tex] é a probabilidade do evento complementar [tex]\overline{E}[/tex], ou simplesmente probabilidade complementar de [tex]P[/tex], e temos a seguinte relação: [tex]\boxed{P+Q=1}\, .[/tex]
✐ Princípio Fundamental da Contagem, ou Princípio Multiplicativo, para [tex]k [/tex] eventos: Se
- um evento E1 puder ocorrer de [tex] m_1 [/tex] maneiras,
- um evento E2 puder ocorrer de [tex]m_2 [/tex] maneiras,
- [tex]\cdots[/tex]
- um evento Ek puder ocorrer de [tex]m_k [/tex] maneiras
e todos esses eventos forem independentes entre si (isto é, a ocorrência de um não muda a quantidade de possibilidades para a ocorrência de outro), então a quantidade de maneiras em que os [tex]k[/tex] eventos ocorrem ao mesmo tempo é:
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
Vamos resolver este problema usando probabilidade complementar, ou seja, vamos calcular a chance de Jorge não conseguir a senha sem bloquear o computador. Assim, ele deverá errar todas as três tentativas.
Como Jorge tem certeza de que o último algarismo da sua senha não é o zero, existem nove opções para esse último algarismo. Assim, observe que:
- Como há [tex]9[/tex] opções e apenas uma é correta, há [tex]8[/tex] escolhas erradas para a primeira tentativa de Jorge.
- Na segunda tentativa, Jorge terá [tex]8[/tex] opções, sendo exatamente [tex]7[/tex] erradas.
- Finalmente, há [tex]6[/tex] possibilidades de Jorge errar na última tentativa, dentre [tex]7[/tex] opções restantes.
Dessa forma, pelo Princípio Fundamental da Contagem, há [tex]9\cdot 8\cdot 7[/tex] possibilidades de escolha, sendo [tex]{8\cdot 7}\cdot 6[/tex] erradas. Assim, o computador será bloqueado com chance de [tex]\dfrac{\cancel{8\cdot 7}\cdot 6}{9\cdot\cancel{ 8\cdot 7}}=\dfrac{6}{9}=\dfrac{2}{3}[/tex].
Portanto, a chance de Jorge acertar a senha, sem bloquear o computador, é de
[tex]\qquad 1-\dfrac{2}{3}=\dfrac{1}{3}[/tex],
ou seja, aproximadamente [tex]\fcolorbox{black}{#eee0e5}{$33,33\%$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
