Problema
(Indicado a partir do 2º ano do E. M.)
(Extraído de: Análise Combinatória, Plínio de Oliveira Santos) De quantos modos oito casais fixos podem sentar-se em uma roda gigante com oito bancos de dois lugares cada um, sendo que cada casal deve sentar em um banco?

AJUDA 1
Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas e
- todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então o número total de maneiras de tomarmos sucessivamente essas [tex]k[/tex] decisões é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)

AJUDA 2
Antes de resolvermos o problema proposto, vamos resolver um problema mais simples envolvendo posições em uma roda.
(*) André, Bené, Cecé e Dedé sentam-se em uma mesa circular para colocar o papo em dia. De quantas maneiras diferentes os quatro amigos poderiam se sentar?
Um raciocínio quase imediato para se resolver o problema (*) seria este:
- Fixado um primeiro lugar na mesa, este poderá ser ocupado por qualquer um dos quatro amigos.
- O próximo lugar poderá ser ocupado por três dos quatro amigos; afinal um deles já está sentado.
- Um terceiro lugar poderá ser ocupado por dois dos quatro amigos, pois dois amigos já estão sentados.
- O último lugar deverá ser ocupado pelo único amigo que ainda não sentou.
Assim os amigos poderão se sentar de [tex]4 \times 3 \times 2 \times 1=24 [/tex] maneiras distintas. Correto?
NÃÃÃÃÃÃÃÃÃÃÃÃÃÃÃÃÃO!
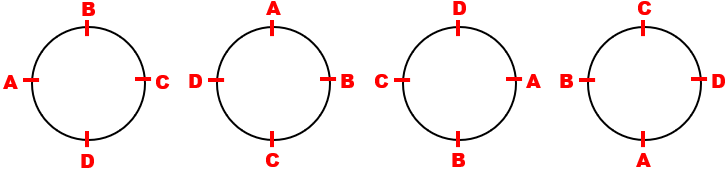
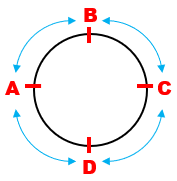
Observe que no problema (*) não está em questão algum tipo de referencial que não seja as quatro posições que cada amigo ocupará na mesa. Dessa forma, o problema só prevê a posição relativa entre eles e não posições que permitam a observação de uma porta ou de uma janela ou que diferenciem a cor das cadeiras em que cada amigo irá sentar, por exemplo. Assim, se representarmos cada um dos quatro amigos pela letra inicial de seu nome, devemos considerar que as quatro formações abaixo são as mesmas,
|
já que os amigos que estão sentados à direita e à esquerda de André, Bené, Cecé e Dedé são sempre os mesmos em qualquer uma das quatro formações:
Então, nessa situação circular as sequências indicadas por |
 |
- [tex]A\,;\,B\,;\,C\,;\,D[/tex]
- [tex]D\,;\,A \,;\,B\,;\,C[/tex]
- [tex]C\,;\,D \,;\,A\,;\,B[/tex]
- [tex]B\,;\,C\,;\,D\,;\,A[/tex]
representam uma mesma formação e portanto devem ser contadas como uma única possível solução do problema (*) e não como quatro soluções.
A maneira como contamos o número de posições em que os quatro irão sentar ([tex]4[/tex], [tex]3[/tex], [tex]2 [/tex] e [tex]1[/tex]) caracterizaria a situação na qual os amigos se posicionariam em filas. No posicionamento em filas, as quatro sequências indicadas representam situações (filas) diferentes, conforme nos mostra a próxima figura.
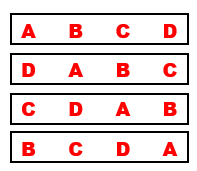
- Com a primeira sequência, André e Dedé só têm um vizinho;
- Com a segunda sequência, Dedé e Cecé só têm um vizinho;
- Com a terceira sequência, Cecé e Bené só têm um vizinho;
- Com a quarta sequência, Bené e André só têm um vizinho.
É importante entender isso para perceber que no cálculo que fizemos quadruplicamos o número de situações que realmente interessam para a solução do problema (*). Portanto, a resposta desse problema é:
- [tex]\dfrac{4 \times 3 \times 2 \times 1}{4}=\dfrac{24}{4}=6[/tex],
ou, se você sabe o que é fatorial de um número natural,
- [tex]\dfrac {4!}{4}=3!\,[/tex].
Essa sutil observação diferencia dois objetos matemáticos distintos: "permutação simples " e "permutação circular". Em um problema de ordenação de elementos devemos utilizar:
- permutações simples, se o problema leva em consideração os lugares que os elementos vão ocupar;
- permutações circulares, se o problema leva em consideração a posição relativa que os elementos ocupam entre si. Nesse caso, duas disposições serão consideradas iguais quando elas coincidem depois de feita uma rotação.
A generalização da nossa observação para um conjunto de [tex]n[/tex] elementos nos garante que:
► O número de permutações simples dos elementos [tex]a_1,\, a_2,\,a_3,\,\dots\, ,\, a_n\,[/tex] é dado por:
[tex]\qquad \qquad \boxed{P_n=n\cdot (n-1) \cdot (n-2) \cdot\, \cdots \, 3 \cdot 2 \cdot 1 \,} [/tex] ou, utilizando fatorial, [tex]\boxed{P_n=n!}[/tex].
► O número de permutações circulares dos elementos [tex]a_1,\, a_2,\,a_3,\,\dots\, ,\, a_n\,[/tex] é dado por:
[tex]\qquad \qquad \boxed{\left(PC\right)_n=(n-1) \cdot (n-2) \cdot\, \cdots \, 3 \cdot 2 \cdot 1 \,} [/tex] ou, utilizando fatorial, [tex]\boxed{\left(PC\right)_n=(n-1)!}[/tex].
Solução
- Segundo a discussão apresentada na AJUDA 2, podemos sentar os [tex] 8[/tex] casais em uma roda gigante de [tex] (8-1)! =7![/tex] maneiras distintas.
- Entretanto, em cada banco, o casal pode se sentar de [tex]2 [/tex] maneiras.
Portanto, segue do Princípio Multiplicativo, AJUDA 1, que temos um total de [tex]~\fcolorbox{black}{#eee0e5}{$7! \cdot 2^8$} [/tex] modos de dispormos os oito casais na roda gigante.
Solução elaborada pelos Moderadores do Blog.
