Probleminha: Cálculo da produção trimestral de automóveis da marca X em 2017

Problema
(Indicado a partir do 8º ano do E. F.)

(TROTA, IMENES & JAKUBOVIC, Matemática Aplicada, volume 1, 2° grau, São Paulo: Moderna, 1979 – Adaptado) Uma fábrica de automóveis produziu $36$ mil unidades de um certo automóvel da marca $X$ no ano de $2017$, de forma que, neste mesmo ano, sua produção dobrou a cada trimestre.
Quantas unidades de automóveis da marca $X$ a fábrica produziu no primeiro trimestre?

Solução 1

Seja $a_1$ a produção de automóveis da marca $X$ no primeiro trimestre de $2017.$ Dessa forma, temos que:

• $2a_1$ é a produção no segundo trimestre de $2017;$
• $4a_1$ é a produção no terceiro trimestre de $2017;$
• $8a_1$ é a produção no quarto trimestre de $2017.$

Como a fábrica produziu $36$ mil unidades desse tipo de automóvel em $2017$, segue que:
$\qquad a_1+2a_1+4a_1+8a_1=36000$
$\qquad 15a_1=36000$
$\qquad a_1=\dfrac{36000}{15}\\ \qquad a_1=2400.$
Portanto, a fábrica em questão produziu $\, \fcolorbox{black}{#eee0e5}{$2 \, 400$} \,$ unidades de automóveis da marca $X$ no primeiro trimestre de $2017.$

Solução elaborada pelos Moderadores do Blog.

Solução 2

Se você ainda não aprendeu a resolver este tipo de problema na forma da Solução 1, apresentaremos uma solução utilizando uma maneira diferente de resolver problemas do 1º grau.

• Como a produção trimestral do ano de $2017$ é $36\ 000$ desenhamos um retângulo e dentro dele colocamos o valor $36\ 000$, que é a quantidade de automóveis da marca $X$ produzidos no ano de $2017.$



• Vamos dividir o ano de $2017$ em quatro trimestres e a produção do primeiro trimestre será representada por um “quadradinho”.
• A produção do segundo trimestre é o dobro da produção do primeiro trimestre e, portanto, será representada por dois quadradinhos.
• Já a produção do terceiro trimestre é o dobro da produção do segundo trimestre e, consequentemente, será representada por $2 \times2=4$ quadradinhos.
• Por fim, a produção do último trimestre será representada por $2 \times 4=8$ quadradinhos.

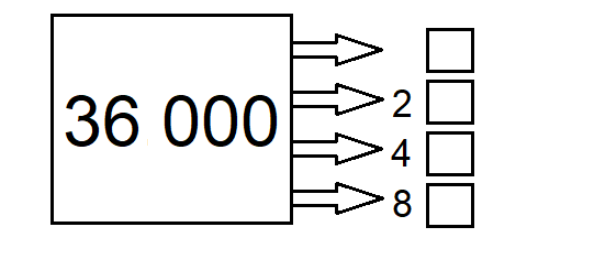
Observe que devemos distribuir as $36\ 000$ unidades entre os $1+2+4+8=15$ quadradinhos representados, obtendo assim o valor de $\dfrac{36000}{15}=2400$ unidades para cada quadradinho.

Logo, a produção de automóveis da marca $X$ pela fábrica no primeiro trimestre de $2017$ foi de $\, \fcolorbox{black}{#eee0e5}{$2 \, 400$} \,$ unidades.

Solução elaborada pelos Moderadores do Blog.