Problema
(UNIFOR: Prova Medicina-2016)
A empresa Ciclos produz dois tipos de bicicletas: Veloz e Rapidez. As possíveis quantidades [tex]x[/tex] de bicicletas Veloz e [tex]y[/tex] de bicicletas Rapidez produzidas anualmente (em milhares) estão relacionadas pela equação chamada de “Curva de Transformação de Produtos”:
[tex]\qquad \qquad 100x^2+9y^2-1200x-216y+3996=0.[/tex]
Qual a soma das quantidades máximas (em milhares) de cada tipo de bicicleta que podem ser fabricadas anualmente?
 |
Para resolver este problema, você pode precisar de um processo conhecido como “completamento de quadrado”. |
Solução 1
(Indicada a partir do 1º ano do E. M.)
Na expressão dada, faremos dois completamentos de quadrados:
[tex]\quad 100x^2+9y^2-1200x-216y+3996=0[/tex]
[tex]\quad (100x^2-1200x)+(9y^2-216y)+3996=0[/tex]
[tex]\quad (100x^2-1200x+\textcolor{red}{3600})+(9y^2-216y+\textcolor{blue}{1296})+3996=0+\textcolor{red}{3600}+\textcolor{blue}{1296}[/tex]
[tex]\quad (10x-60)^2+(3y-36)^2=3600+1296-3996=900[/tex].
[tex]\quad (10x-60)^2+(3y-36)^2=30^2[/tex].
-
Agora, perceba que [tex]x[/tex] será máximo quando [tex]3y-36=0[/tex]; assim, para que [tex]x[/tex] seja máximo devemos ter:
[tex]\qquad (10x-60)^2=30^2[/tex]
[tex]\qquad \sqrt{(10x-60)^2}= \sqrt{30^2}[/tex]
[tex]\qquad |10x-60|=30 [/tex]
[tex]\qquad 10x-60=\pm30. \qquad \textcolor{#800000}{(i)}[/tex]
Em [tex] \textcolor{#800000}{(i)}[/tex] temos duas igualdades: [tex]10x-60=30 [/tex] e [tex]10x-60=-30 [/tex].
A primeira nos fornece [tex]x=9[/tex] e, a segunda, [tex]x=3[/tex]; como busca-se a maior quantidade, ficamos só com a possibilidade [tex]\boxed{x=9} \, .[/tex]
-
Da mesma forma, [tex]y[/tex] será máximo quando [tex]10x-60=0[/tex]; assim, também devemos ter:
[tex]\qquad (3y-36)^2=30^2[/tex]
[tex]\qquad \sqrt{(3y-36)^2}=\sqrt{30^2}[/tex]
[tex]\qquad |3y-36|=30[/tex]
[tex]\qquad 3y-36=\pm 30. \qquad \textcolor{#800000}{(ii)} [/tex]
Também temos duas igualdades em [tex] \textcolor{#800000}{(ii)}[/tex]: [tex]3y-36=30 [/tex] e [tex]3y-36=-30 [/tex].
A primeira tem como resposta [tex]y=22[/tex] e, a segunda, [tex]x=2[/tex]. Mais uma vez, buscamos a maior quantidade; assim, ficamos apenas com a possibilidade [tex] \boxed{y=22} \, .[/tex]
Finalizando o problema, segue que [tex]\fcolorbox{black}{#eee0e5}{$x+y=9+22=31$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
(Indicada a partir do 3º ano do E. M.)
Para quem já estudou cônicas, uma solução geométrica poderia ser feita a partir dos completamentos de quadrado feitos no início da Solução 1. Vejamos.
De [tex](10x-60)^2+(3y-36)^2=30^2[/tex], segue que:
[tex]\qquad \dfrac{(10x-60)^2}{30^2}+\dfrac{(3y-36)^2}{30^2}=1[/tex]
[tex]\qquad \left(\dfrac{10x-60}{30}\right)^2+\left(\dfrac{3y-36}{30}\right)^2=1[/tex]
[tex]\qquad \left(\dfrac{x-6}{3}\right)^2+\left(\dfrac{y-12}{10}\right)^2=1[/tex]
[tex]\qquad\boxed{\dfrac{(x-6)^2}{9}+\dfrac{(y-12)^2}{100}=1} \qquad \textcolor{#800000}{(iii)}[/tex]
- A equação [tex]\textcolor{#800000}{(iii)}[/tex] descreve uma elipse centrada no ponto [tex](6, 12)[/tex] do sistema ortogonal de coordenadas [tex]xOy[/tex], com medidas de eixos [tex]a = 6[/tex] e [tex]b = 20[/tex] e cujo eixo maior é vertical.
O ponto de ordenada máxima é [tex]\, (6, 12) + (0, 10) = (6, \textcolor {red}{22}) [/tex] e o de abscissa máxima é [tex]\, (6, 12) + (3, 0) = (\textcolor {red}{9}, 12) [/tex], conforme podemos ver na figura abaixo.
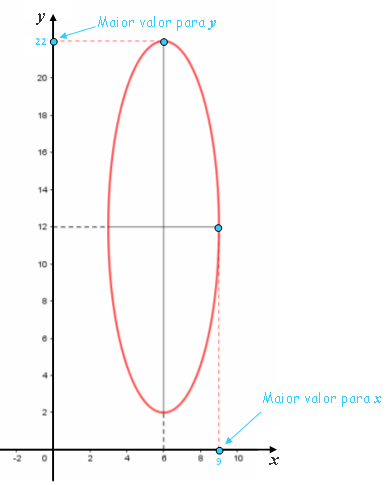
Assim, [tex] \boxed{x_{max}=6} \, [/tex], [tex] \boxed{y_{max}=22} \, [/tex] e, portanto, a resposta do problema é [tex]\fcolorbox{black}{#eee0e5}{$x_{max}+y_{max}=9+22=31$} \, .[/tex]
Uma observação final: a figura nos mostra que esses dois máximos não ocorrem simultaneamente!
Solução elaborada pelos Moderadores do Blog.
