.Problemão: Um quadrado e vários círculos

Problema
(Indicado a partir do 9º ano do E. F.)

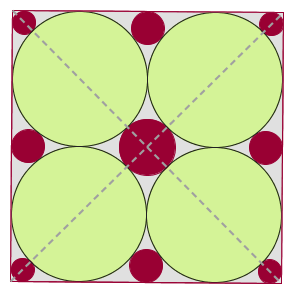
Temos um quadrado e quatro círculos verdes grandes cujos diâmetros medem a metade do lado do quadrado, como indicados na figura.

Como encontrar, por processos puramente geométricos (isto é, utilizando régua e compasso), os centros e os raios dos círculos restantes?

Dicas

• Para o maior deles (o círculo central), não é difícil localizar o centro (feito isso, determinar o raio com o compasso também não será difícil).
• Para os menores (nos cantos), uma ideia é observar que o centro deve estar à mesma distância do lado do quadrado e do ponto de tangência com o círculo verde. Isso remete a um outro lugar geométrico precioso: a bissetriz (Mas de qual ângulo?).
• Para os intermediários (nas laterais), comece observando que o centro deve estar sobre as retas que passam pelos pontos médios dos lados do quadrado. O resto? Pense um pouquinho mais.

Solução

http://pt.wikipedia.org/wiki/Bissetriz.

Mas você também pode executar essa construção com um applet, clicando no botão abaixo.

(1) Com a construção da bissetriz do ângulo de vértice $O$, observe que ficam definidos os triângulos $\triangle OAC$ (em alaranjado) e $\triangle OBC$ (em verde), conforme mostra a figura a seguir na qual denotamos por a e b as semirretas definidas pelos pontos ”$O$ e $A$” e ”$O$ e $B$”, respectivamente.



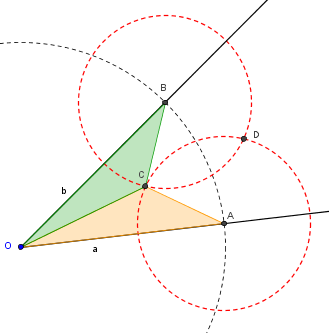
Note que os triângulos $\triangle OAC$ e $\triangle OBC$ são congruentes (iguais), já que eles têm todos lados congruentes (convença-se disso).
Da mesma forma, temos que $\triangle OAD$ e $\triangle OBD$. Assim, temos que os ângulos $\angle BOC$ e $\angle AOC$ são também congruentes e, portanto, a reta que passa por $O$ e $C$ (e também por $D$) está bem definida e é, de fato, a bissetriz de $\angle AOB$.
(2) Podemos também garantir que as distâncias de $C$ às semirretas a e b são também iguais (o mesmo poderia ser dito com relação ao ponto $D$ ou qualquer outro ponto sobre a bissetriz em questão). Para justificar essa afirmação, tomamos as perpendiculares às semirretas a e b que passam por $C$ e marcamos na figura abaixo os pontos de intersecção por, respectivamente, por $M$ e $N$.

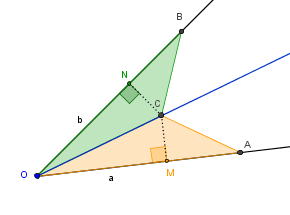
Observe que $\triangle OMC \equiv \triangle ONC$ (temos dois triângulos retângulos com ângulos iguais e hipotenusas comuns) e, portanto, as distâncias $CM$ e $CN$ são iguais.

$\bullet$ Centro e raio do círculo central:
Para determinarmos o centro deste círculo, basta tomarmos o ponto de intersecção entre as diagonais do quadrado; o raio, neste caso, é a medida do centro ao ponto de intersecção da circunferência com uma das diagonais do quadrado.

$\bullet$ Centro e raio dos círculos menores:
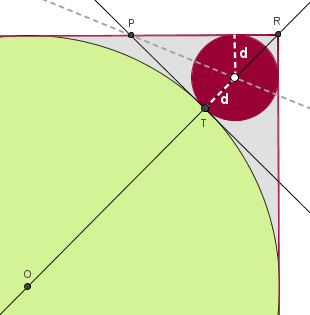
Inicialmente, observemos que o centro de qualquer um dos círculos de interesse estará à mesma distância d do lado superior do quadrado e do ponto de tangência $T$ entre os círculos roxo e verde. O ponto $T$ nada mais é do que a intersecção entre a diagonal do quadrado e as circunferências em questão.

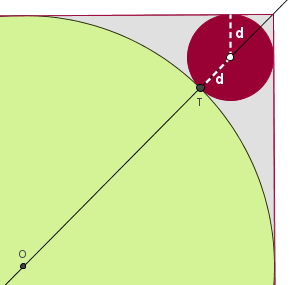
Logo, se traçarmos a reta tangente aos círculos em $T$ (para isto, basta tomarmos uma perpendicular à diagonal, passando por $T$ – se você não sabe como construir uma perpendicular com régua e compasso, pode visitar a solução do problema “Usando régua e compasso”, que está disponível nas nossas Salas de Problemas), constatamos que o ponto desejado deve estar à mesma distância dos lados $\overline{PT}$ e $\overline{PR}$ do triângulo $PRT$, ou seja, para determiná-lo devemos tomar o ponto de intersecção entre a diagonal e a bissetriz de $\angle TPR$. Para o raio, basta considerar a distância do centro do círculo em questão até o ponto $T$.

$\bullet$ Centro e raio dos círculos intermediários:
Mais uma vez, o ideal é que observemos que propriedades terá o ponto que procuramos determinar. Naturalmente que o centro do círculo de interesse estará sobre a reta que passa pelos pontos médios dos lados paralelos do quadrado. Além disso, note que ele estará à mesma distância dos centros dos círculos verdes (que podem ser facilmente determinados pelas intersecções das retas que passam pelos quartos dos lados paralelos do quadrado).

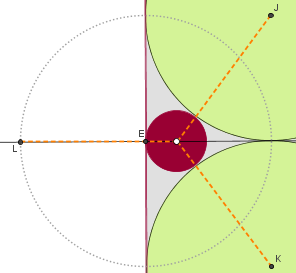
Sendo assim, com a medida do raio dos círculos verdes, a partir do ponto $E$ (ponto de intersecção entre o lado do quadrado e a reta que passa pelo pontos médios de seus lados), marcamos o ponto $L$, que estará, então, à mesma distância do centro do círculo (roxo), em relação aos centros $J$ e $K$ dos círculos verdes. Finalmente, construímos a mediatriz do segmento $\overline{LK}$ e teremos o centro do círculo procurado (para entender melhor por que a mediatriz resolve, você pode consultar a resolução do problema “Usando régua e compasso” já referenciada anteriormente). Para o raio, basta tomar a medida do centro até o ponto $E$.

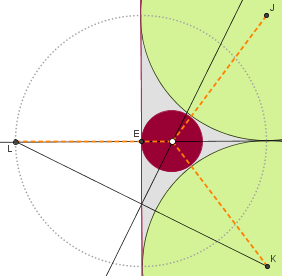
Solução elaborada pelos Moderadores do Blog.