Problema
(Indicado a partir do 9º ano do E. F.)
Os ponteiros de um relógio se superpõem várias vezes ao dia.
Qual o intervalo de tempo entre duas superposições consecutivas?
Solução 1
Ao meio-dia em ponto, os ponteiros estão sobrepostos. Após mais de [tex]65[/tex] minutos e menos de [tex]70[/tex] minutos eles estarão sobrepostos novamente.
Sejam [tex]t[/tex] o tempo medido em minutos, contado a partir de uma hora em ponto, [tex]v[/tex] a velocidade angular do ponteiro das horas e [tex]V[/tex] a dos minutos. Definimos também [tex]\theta_1\,[/tex] e [tex]\,\theta_2[/tex] como sendo o ângulo formado pelo ponteiro das horas e o ângulo formado pelo ponteiro dos minutos, respectivamente, após [tex]t[/tex] minutos. Assim, [tex]v=\dfrac{\pi}{360}[/tex] rad/min e [tex]V=\dfrac{2\pi}{60}[/tex] rad/min. Podemos escrever:
[tex]\qquad \theta_1=\dfrac{\pi}{6}+\dfrac{\pi}{360}t \qquad \qquad \qquad (1)[/tex]
[tex]\qquad \theta_2=\dfrac{2\pi}{60}t\,. \qquad \qquad \qquad \qquad (2)[/tex]
Como queremos que os dois ângulos [tex]\theta_1[/tex] e [tex]\theta_2[/tex] sejam iguais, temos que:
[tex]\qquad \dfrac{\pi}{6}+\dfrac{\pi}{360}t=\dfrac{2\pi}{60}t \\
\qquad t=\dfrac{60}{11}\\
\qquad t\approx 5~ minutos~ e ~ 27~segundos.[/tex]
Portanto, as superposições consecutivas se darão, aproximadamente, a cada [tex]1[/tex] hora, [tex]5[/tex] minutos, [tex]27[/tex] segundos.
Solução elaborada pelos Moderadores do Blog.
Solução 2
À meia noite em ponto, os ponteiros estão sobrepostos, assim a próxima sobreposição será entre 1h e 2h.
Veja, então, as posições dos ponteiros dos relógios exatamente à 1h e no momento da sobreposição entre 1h e 2h.
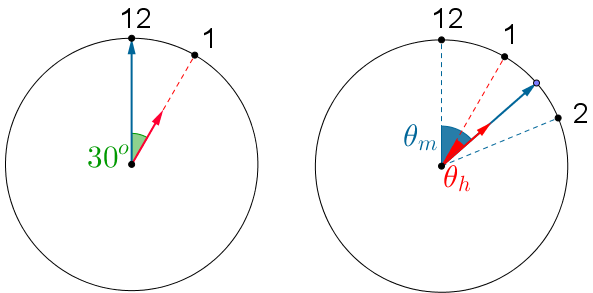
Observe que, de 1h até o momento da sobreposição, se ponteiro das horas girou [tex]x[/tex] graus, então o ponteiro dos minutos girou, em graus, [tex]30 + x[/tex].
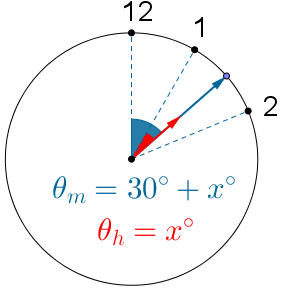
Por outro lado, sabemos que enquanto o ponteiro das horas gira [tex]30^{\circ}[/tex], o dos minutos gira [tex]360^{\circ}[/tex];
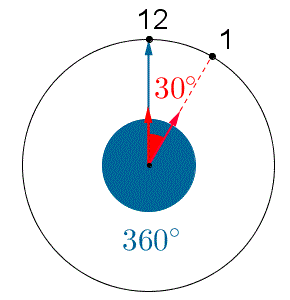
assim, temos a seguinte regra de três, em graus:
Horas Minutos
[tex]30[/tex] [tex]360[/tex]
[tex]x[/tex] [tex]30+x[/tex]
Dessa forma,
[tex]\qquad 30(30+x) =360x \\
\qquad 30+x =12x\\
\qquad 30=11x\\
\qquad x=\dfrac{30}{11}.\\[/tex]
Para determinarmos depois de quantos minutos, após a 1h, ocorreu a transposição, basta considerarmos a seguinte regra de três, na qual os ângulos estão expressos em graus e o tempo em minutos:
Tempo Ângulo do ponteiro das horas
[tex]60[/tex] [tex]\qquad 30[/tex]
[tex]t[/tex] [tex]\qquad \dfrac{30}{11}[/tex]
Com isso,
[tex]\qquad 60\cdot \dfrac{30}{11} =30t \\
\qquad \\
\qquad \dfrac{60}{11} =t\\
\qquad t=\dfrac{55}{11}+\dfrac{5}{11} \\
\qquad t=\left(5+\dfrac{5}{11} \right)\, minutos\,.[/tex]
Agora, observe que
[tex]\qquad \dfrac{5}{11}\, minutos=\dfrac{5}{11}\times 60 \, segundos=\dfrac{300}{11}\, segundos\approx 27,27\, segundos[/tex];
logo,
[tex]\qquad t\approx 5\, minutos\, e\, \, 27\, segundos.
\, \\[/tex]
Portanto, as superposições consecutivas se darão, aproximadamente, a cada [tex]1[/tex] hora, [tex]5[/tex] minutos e [tex]27[/tex] segundos.
Solução elaborada pelos Moderadores do Blog.
