Problema
Sejam
[tex]\qquad S_1=\{(x,y) \in\mathbb{R}^2: x^2+y^2+4y-32\leqslant 0\}[/tex]
e
[tex]\qquad S_2=\{(x,y) \in\mathbb{R}^2:y\geqslant ||x|-2| \}[/tex].
Determine a área da região que representa [tex]S_1\cap S_2[/tex] no plano cartesiano [tex]xOy[/tex].
Solução
[tex]\textcolor{#800000}{(1)}[/tex] Consideremos inicialmente a região [tex]S_1=\{(x,y) \in\mathbb{R}^2: x^2+y^2+4y-32\leqslant 0\}.[/tex]
Utilizaremos a técnica de “completar o quadrado” para que possamos colocar a inequação que define [tex]S_1[/tex] numa forma mais apropriada e, então, determinar que tipo de região ela define. (Se você não se lembra dos detalhes dessa técnica, visite esta Sala de Leitura.) Observe:
[tex]\qquad x^2+y^2+4y-32\leqslant 0 \iff[/tex]
[tex]\qquad x^2+y^2+4y+(4-4)-32\leqslant 0 \iff[/tex]
[tex]\qquad x^2+y^2+4y+4\leqslant 36 \iff[/tex]
[tex]\qquad x^2+(y-(-2))^2\leqslant 6^2.\qquad \textcolor{#800000}{(i)}[/tex]
A desigualdade [tex]\textcolor{#800000}{(i)}[/tex] define um disco de centro no ponto [tex]C=(0,-2)[/tex] e raio [tex]6[/tex]; assim,
- a região [tex]S_1[/tex] corresponde à circunferência de centro em [tex](0,-2)[/tex] e raio [tex]6[/tex] e sua parte interna.[tex]\qquad \textcolor{#800000}{(ii)}[/tex]
[tex]\textcolor{#800000}{(2)}[/tex] Para determinar a região [tex]S_2=\{(x,y) \in\mathbb{R}^2:y\geqslant ||x|-2| \}[/tex], vamos aplicar uma sequência de transformações para obter a “curva” definida pela equação [tex]y= ||x|-2|.[/tex] Vamos lá!
- Por definição, temos que:
[tex]\qquad |x|=\left\{\begin{array}{cc} x \, ,&\text{se} \quad x\geqslant 0\\-x \, ,&\text{se}\quad x\lt 0\end{array}\right. \, [/tex];
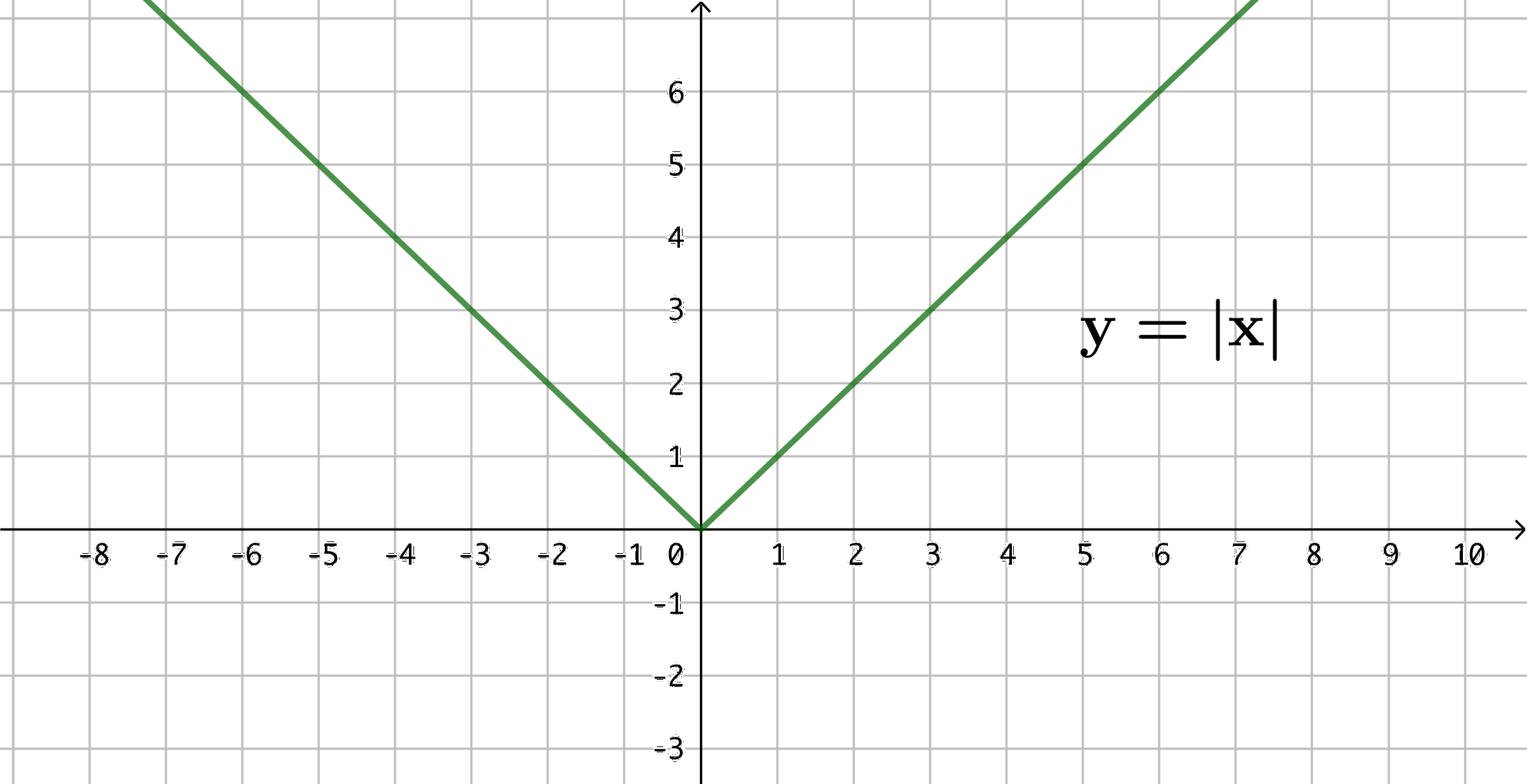
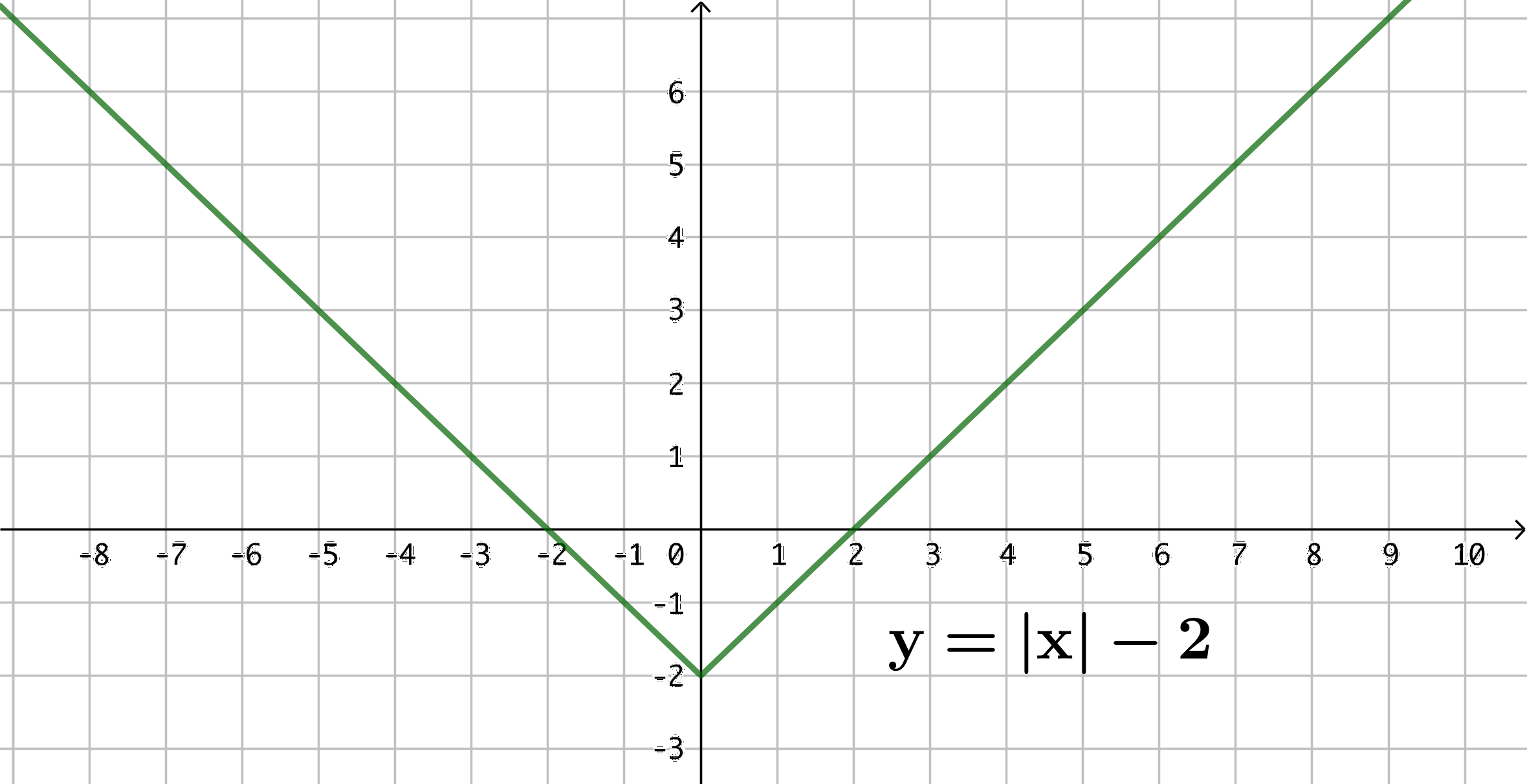
assim, a equação [tex]y=|x|[/tex] define o gráfico mostrado a seguir. - A partir do gráfico anterior, podemos obter o gráfico definido pela igualdade [tex]y=|x|-2[/tex]. Para isso, perceba que para cada valor real de [tex]x[/tex] a igualdade [tex]y=|x|-2[/tex] fornece para [tex]y[/tex] o valor que a igualdade [tex]y=|x|[/tex] fornece diminuído de duas unidades. Assim, o gráfico definido pela igualdade [tex]y=|x|-2[/tex] é o gráfico anterior transladado de duas unidades para baixo.
- Por fim, consideremos a igualdade que nos interessa: [tex]y=||x|-2|[/tex].
Note que, ao aplicarmos o valor absoluto na expressão [tex]|x|-2[/tex], não alteramos o seu valor quando este for não negativo e “transformamos” em positivo o que era negativo. Podemos visualizar graficamente isso, mantendo a parte do gráfico anterior que está acima do eixo [tex]Ox[/tex] e refletindo para cima a parte que está abaixo do eixo. Observe: - a região [tex]S_2[/tex] corresponde aos pontos da linha poligonal do gráfico anterior e aos pontos que estão acima dessa poligonal.[tex]\qquad \textcolor{#800000}{(iii)}[/tex]
Observe que a "quina" formada nesse gráfico define um ângulo de [tex]90^\circ[/tex] e que os segmentos abaixo do eixo [tex]Ox[/tex] são a metade de um quadrado, já que ambos possuem o mesmo comprimento.
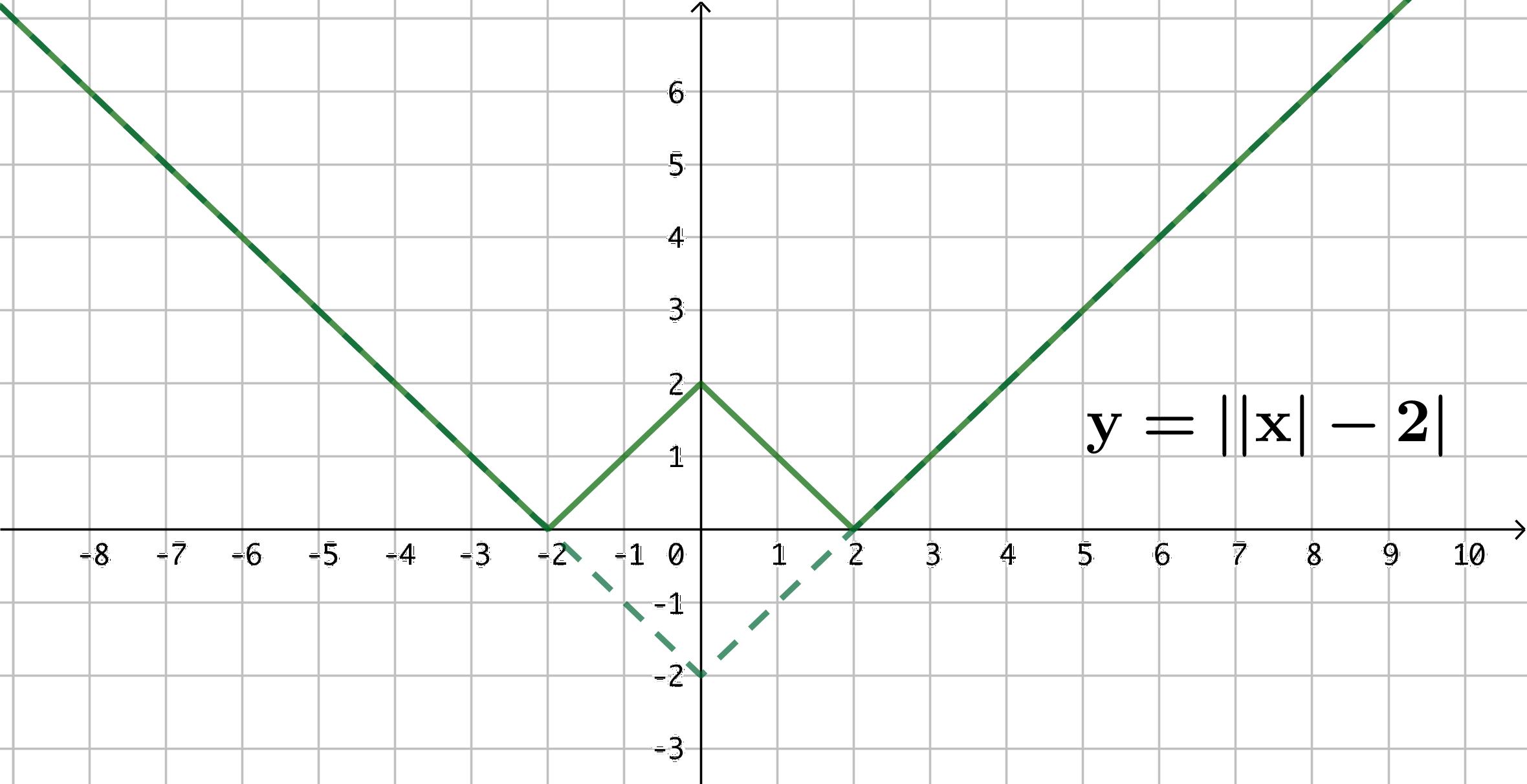
Mas, a região [tex]S_2[/tex] é definida por [tex]S_2=\{(x,y) \in\mathbb{R}^2:y\ge ||x|-2| \}[/tex] e os pontos na linha poligonal do gráfico anterior identificam os pontos [tex](x,y)[/tex] tais que [tex]y=||x|-2|[/tex]. Dessa forma, os pontos cujas coordenadas satisfazem a desigualdade [tex]y\gt ||x|-2|[/tex] são aqueles acima da poligonal e, portanto,
Analisando as informações [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], temos que a região que nos interessa, [tex]S_1\cap S_2[/tex], fica graficamente representada por:
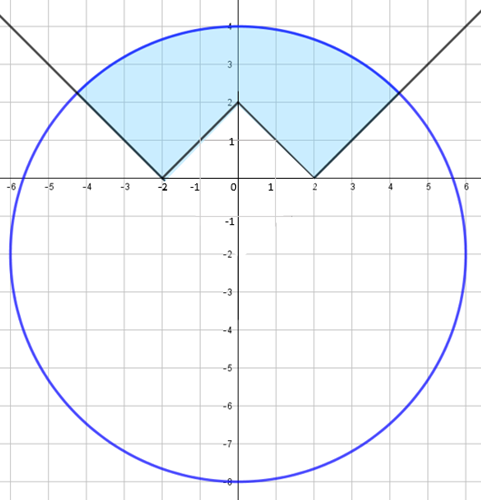
Concluí-se, portanto, que a área da região [tex]S_1\cap S_2[/tex] pode ser obtida retirando-se a área de um quadrado, cuja diagonal mede [tex]4[/tex] unidades, da área correspondente a [tex]\frac{1}{4}[/tex] do círculo [tex]S_1[/tex], conforme a figura abaixo indica.
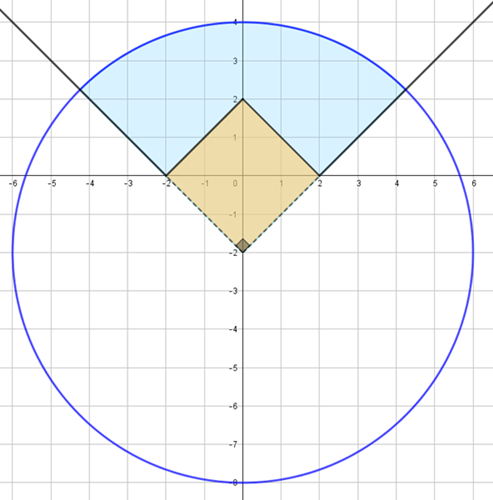
Finalmente, vamos aos cálculos da área da região em questão:
- Aplicando o Teorema de Pitágoras ao triângulo retângulo formado pelos lados do quadrado e sua diagonal obtemos:
[tex]\qquad l^2+l^2=d^2[/tex]
[tex]\qquad 2l^2=4^2[/tex]
[tex]\qquad l^2=8[/tex].
Portanto, temos que a área do quadrado é [tex]\boxed{A_q=l^2=8} \, .[/tex] - Para a circunferência, sabemos que
[tex]\qquad A_c=\pi\times r^2=\pi\times6^2=36\pi \, .[/tex]
Por tudo o que foi exposto, a área da região [tex]S_1\cap S_2[/tex] é dada por [tex] \, \, \fcolorbox{black}{#eee0e5}{$A_{S_1\cap S_2}=\frac{1}{4}\cdot 36\pi-8=9\pi-8\text{ unidades de área}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
