Problema
(Indicado a partir do 9º ano do E. F.)
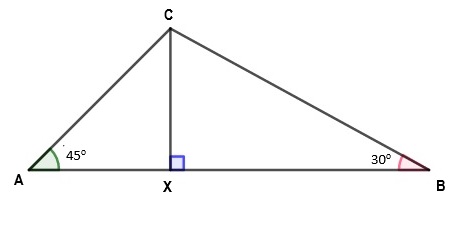
No triângulo da figura abaixo, pelo ponto [tex]X[/tex] trace uma reta paralela ao lado [tex]\overline{BC}[/tex]. Considere [tex]M[/tex] o ponto de interseção dessa reta com o lado [tex]\overline{AC}[/tex].
Calcule a razão entre as medidas dos segmentos [tex]\overline{CM}[/tex] e [tex]\overline{CA}[/tex].
Solução
Notação: Denotaremos um segmento definido por dois pontos, por exemplo pontos [tex]Y[/tex] e [tex]Z[/tex], por [tex]\overline {YZ}[/tex], e sua medida por [tex]YZ[/tex].
Vamos traçar duas retas paralelas ao lado [tex]\overline{BC}[/tex]: uma passando pelo ponto [tex]A[/tex] e outra passando pelo ponto [tex]X.[/tex]
Na reta paralela que passa pelo ponto [tex]X[/tex], obtemos o ponto [tex]M[/tex], interseção entre a reta e o lado [tex]\overline{AC}[/tex]. Veja a figura a seguir.
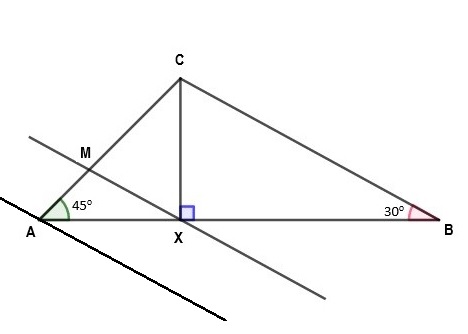
Observe que:
- a reta que passa pelos pontos [tex]B[/tex] e [tex]C[/tex], a reta que passa pelos pontos [tex]X[/tex] e [tex]M[/tex] e a que passa pelo ponto [tex]A[/tex] são paralelas;
- a reta que passa pelos pontos [tex]A[/tex] e [tex]C[/tex] e a reta que passa pelos pontos [tex]A[/tex] e [tex]B[/tex] são transversais às três anteriores;
assim, podemos aplicar o Teorema de Tales, que nos garante que:
- se um feixe de retas paralelas, com no mínimo três retas, é intersetado por duas transversais, os segmentos de retas produzidos pelas paralelas sobre as transversais são proporcionais. (Caso não conheçam ou não se lembrem do Teorema de Tales, cliquem aqui)
Dessa forma,
[tex] \begin{equation}
\dfrac{CM}{CA}=\dfrac{BX}{BA} \, \, .\;\;\;\;\;\;\;\;\;\; (i)
\end{equation}[/tex]
Notemos que o triângulo [tex]BXC[/tex] é retângulo, então
[tex]\begin{equation}tg \;30^{\circ}=\dfrac{CX}{BX}\\
\dfrac{\sqrt{3}}{3}=\dfrac{CX}{BX}
\\BX=\dfrac{3}{\sqrt{3}}CX.\;\;\;\;\;\;\;\;\;\; (ii)
\end{equation}[/tex]
O triângulo [tex]AXC[/tex] também é retângulo, logo
[tex]\begin{equation}tg \;45^{\circ}=\dfrac{CX}{AX}\\
1=\dfrac{CX}{AX}\\
AX=CX. \;\;\;\;\;\;\;\;\;\; (iii)
\end{equation}[/tex]
Vemos que
[tex]\begin{equation}
BA=BX+AX.\;\;\;\;\;\;\;\;\;\; (iv)
\end{equation}[/tex]
Substituindo [tex](ii), \;(iii)[/tex] e [tex](iv)[/tex] em [tex](i)[/tex], segue que:
[tex] \qquad \dfrac{CM}{CA}=\dfrac{BX}{BX+AX}\\
\qquad \dfrac{CM}{CA}=\dfrac{\dfrac{3}{\sqrt{3}}CX}{\dfrac{3}{\sqrt{3}}CX+CX}\\
\qquad \dfrac{CM}{CA}=\dfrac{\dfrac{3}{\sqrt{3}}CX}{\dfrac{3+\sqrt{3}}{\sqrt{3}}CX}\\
\qquad \dfrac{CM}{CA}=\dfrac{3}{3+\sqrt{3}}.[/tex]
Racionalizando o denominador da última igualdade, obtemos
[tex] \qquad \dfrac{CM}{CA}=\dfrac{3(3-\sqrt{3})}{(3+\sqrt{3})(3-\sqrt{3})}\\
\qquad \dfrac{CM}{CA}=\dfrac{3(3-\sqrt{3})}{9-3}\\[/tex]
e, assim, [tex] \, \fcolorbox{black}{#eee0e5}{$ \, \dfrac{CM}{CA}=\dfrac{3-\sqrt{3}}{2}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
