Problema
(Indicado a partir do 9º ano do E. F.)
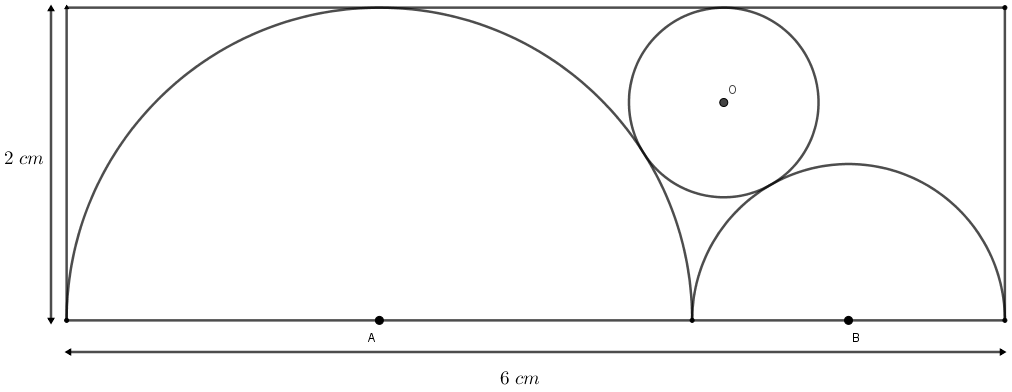
A figura abaixo apresenta um retângulo cujas dimensões medem [tex]2\;cm[/tex] e [tex]6\;cm[/tex], uma semicircunferência de centro [tex]A[/tex] e raio [tex]2\;cm[/tex] e outra semicircunferência de centro [tex]B[/tex] e raio [tex]1\;cm[/tex]. Calcule a medida do raio da circunferência tangente ao retângulo e às semicircunferências.

Lembrete
✏ Heron de Alexandria (± 10 – 70), ou ainda Hero ou Herão, foi um matemático grego. É dele a fórmula que nos permite calcular a área de um triângulo em função das medidas dos seus três lados.
Em um triângulo de lados medindo [tex]a,\, b,\, c[/tex], a fórmula de Herão nos garante que a área [tex]A[/tex] desse triângulo é:
[tex]\qquad \qquad A=\sqrt{p\cdot(p-a)\cdot(p-b)\cdot(p-c)}[/tex],
onde [tex]p[/tex] é o semiperímetro do triângulo em questão, ou seja, [tex]p=\dfrac{a+b+c}{2}\, .[/tex]
– Para rever esse tema, clique AQUI.
– Para aprender um pouco mais sobre esse tema, clique AQUI.
Solução
Inicialmente, vamos construir o triângulo [tex]AOB[/tex]. Sendo [tex]r[/tex] o raio procurado, note que o triângulo construído possui base [tex]AB=3\;cm[/tex] e altura relativa ao lado [tex]AB[/tex] valendo [tex]2-r[/tex].
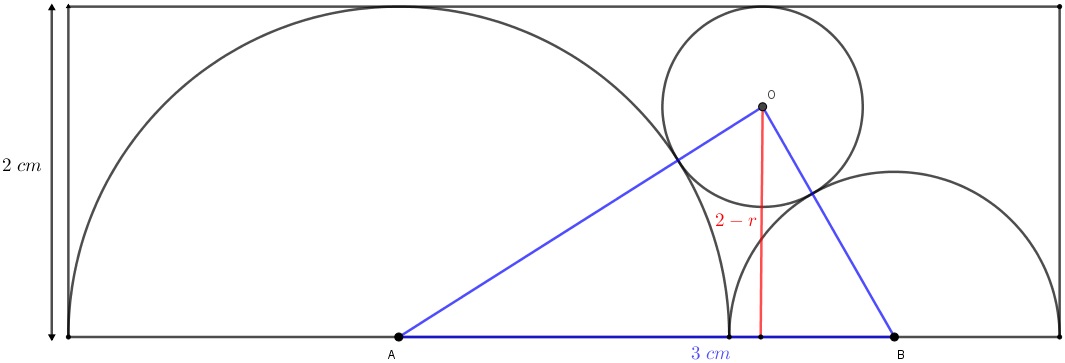
Portanto, a área do triângulo [tex]AOB[/tex] pode ser calculada por:
[tex]\qquad S=\dfrac{3\cdot(2-r)}{2}.\qquad \qquad \textcolor{#800000}{(i)}[/tex]
Porém, o triângulo [tex]AOB[/tex] possui lados [tex]AB=3\;cm[/tex], [tex]AO=2+r[/tex] e [tex]OB=1+r[/tex].
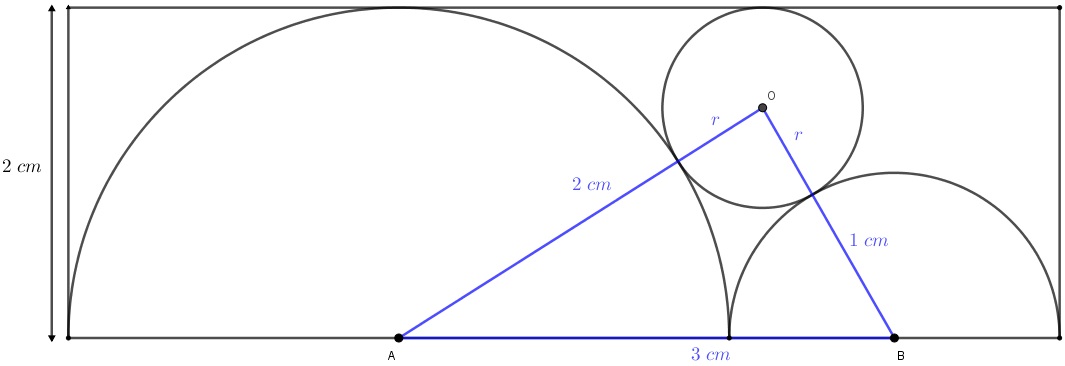
Pelo lembrete, também podemos calcular sua área usando a fórmula de Herão:
[tex]\qquad S=\sqrt{(3+r)\cdot r\cdot 1 \cdot 2}=\sqrt{6r + 2r^{2}}\qquad \qquad \textcolor{#800000}{(ii)}[/tex]
Logo, por [tex]\textcolor{#800000}{(i)}\, [/tex] e [tex]\, \textcolor{#800000}{(ii)}[/tex], segue que:
[tex]\qquad \dfrac{3\cdot(2-r)}{2}=\sqrt{6r + 2r^{2}}[/tex]
[tex]\qquad 3\cdot(2-r)=2\cdot\sqrt{6r + 2r^{2}}[/tex]
[tex]\qquad (3\cdot(2-r))^{2}=(2\cdot\sqrt{6r + 2r^{2}})^2[/tex]
[tex]\qquad 9\cdot(2-r)^{2}=4\cdot\ (6r + 2r^{2})[/tex]
[tex]\qquad 9\cdot(4-4r+r^{2})=24r+8r^{2}[/tex]
[tex]\qquad 36-36r+9r^{2}=24r+8r^{2}[/tex]
[tex]\qquad r^{2}-60r+36=0. \qquad \qquad \textcolor{#800000}{(iii)}[/tex]
A equação [tex]\textcolor{#800000}{(iii)}\, [/tex] é uma equação do 2º grau com discriminante [tex]\Delta = 3456[/tex] e, como [tex]\sqrt{3456}=24\sqrt{6}[/tex], temos que:
[tex]\qquad r= \dfrac{60\pm24\sqrt{6}}{2}[/tex];
donde concluímos que [tex]r=30-12\sqrt{6}[/tex] ou [tex]r=30+12\sqrt{6}.[/tex]
Note que o valor [tex]30+12\sqrt{6}[/tex] não convém para a solução do problema, pois o valor do raio não pode ser maior que o lado do retângulo. Portanto, a medida do raio da circunferência em questão é [tex]\fcolorbox{black}{#eee0e5}{$30-12\sqrt{6}\, cm $}[/tex], ou seja, aproximadamente [tex]\fcolorbox{black}{#eee0e5}{$0,6\; cm $}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
