Problema
(Indicado a partir do 9º ano do E. F.)
(POTI – Curso de Geometria – Nível 2) Quatro quadrados são construídos exteriormente nos lados de um paralelogramo.
Mostre que os centros destes quadrados também formam um quadrado.

Lembrete
Conceitos simples de geometria podem ser de grande utilidade para demonstrar propriedades importantes e/ou interessantes, como na questão aqui proposta.
Nesta questão, pode ser valioso utilizar congruência de triângulos. Para saber um pouco mais acerca desse conteúdo, visitem a página do Blog dos Clubes de Matemática Um pouco sobre congruência de triângulos.
Solução
[tex]\textcolor{#800000}{(1)}[/tex] Sabemos que, em um paralelogramo:
– os lados opostos são congruentes,
– os ângulos opostos são congruentes
– e ainda dois ângulos adjacentes são suplementares.
Assim, podemos representar um paralelogramo genérico e seus ângulos da seguinte forma, supondo [tex]\alpha[/tex] a medida em graus de um de seus ângulos:
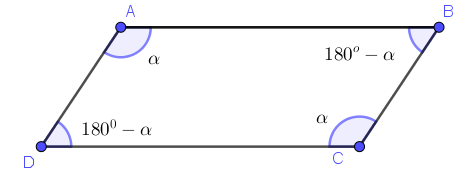
Seja [tex]ABCD[/tex] um paralelogramo.
[tex]\textcolor{#800000}{(2)}[/tex] Construindo quatro quadrados exteriormente aos lados do paralelogramo [tex]ABCD[/tex], obtemos uma figura como a mostrada a seguir.
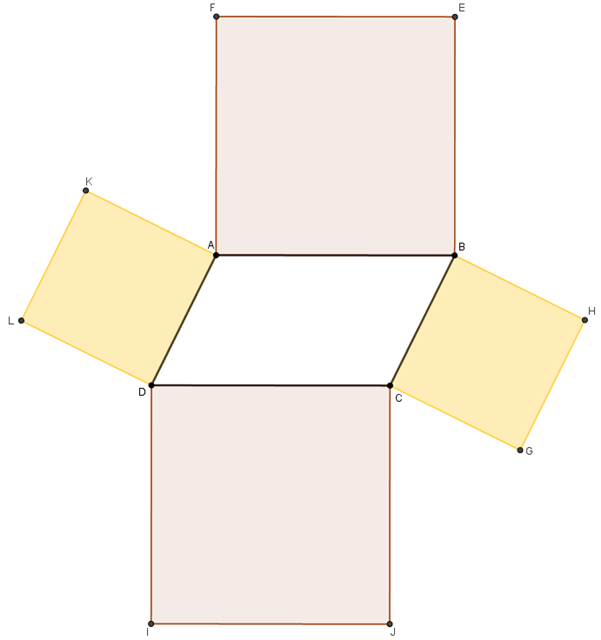
Queremos mostrar que os centros desses quadrados também formam um quadrado. Sejam, então, [tex]M \, ,N \, ,O \, ,P \, [/tex] os centros desses quadrados e considere o quadrilátero [tex]MNOP \, [/tex], conforme ilustrado na figura seguinte.
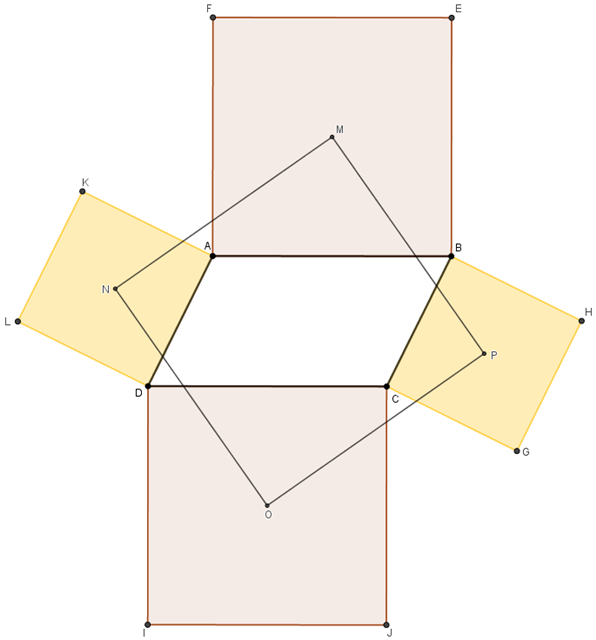
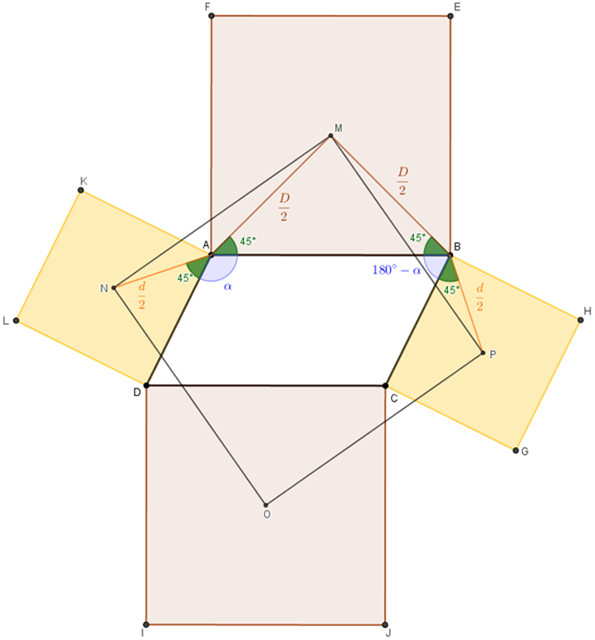
[tex]\textcolor{#800000}{(3)}[/tex] Vamos construir os triângulos [tex]MBP[/tex] e [tex]NAM[/tex]. Note que dois dos lados desses dois triângulos são definidos por metades das diagonais de quadrados construídos em [tex]\textcolor{#800000}{(2)}[/tex]: especificamente, um dos dois quadrados maiores e um dos menores. Na figura abaixo, indicamos os comprimentos das semidiagonais maiores por [tex] \dfrac{D}{2}[/tex] e os das semidiagonais menores por [tex] \dfrac{d}{2} \, .[/tex]
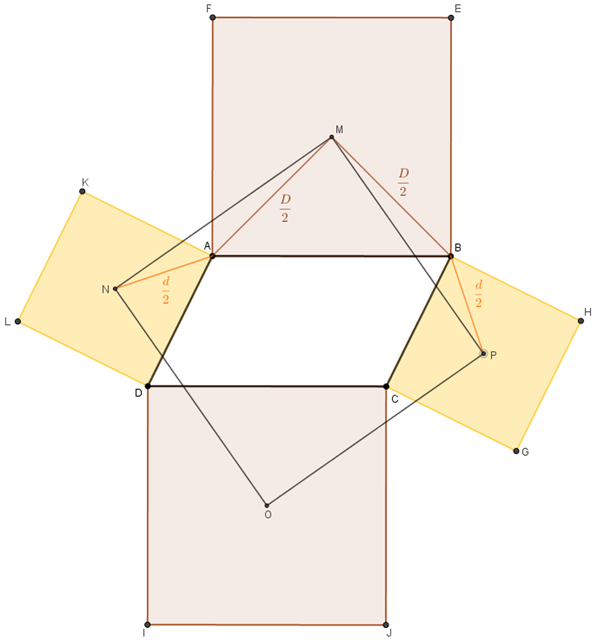
[tex]\textcolor{#800000}{(4)}[/tex] Vamos agora analisar os triângulos [tex]MBP[/tex] e [tex]NAM[/tex].
Utilizando a propriedade dos ângulos do paralelogramo explicitada em [tex]\textcolor{#800000}{(1)}[/tex] e também o fato de que a diagonal de um quadrado também é a bissetriz de um ângulo reto, podemos concluir que:
- a medida do ângulo [tex]M\hat{B}P[/tex] é:
[tex]\quad 45^\circ+\left(180^\circ-\alpha\right)+45^\circ=\boxed{270^\circ-\alpha} \, ; [/tex] - a medida do ângulo [tex]N\hat{A}M[/tex] é
[tex]\quad360^\circ-\left(45^\circ+\alpha+45^\circ\right)=\boxed{270^\circ-\alpha} \, . [/tex]
Dessa forma, pelo caso de congruência lado-ângulo-lado, os triângulos [tex]MBP[/tex] e [tex]MAN[/tex] são congruentes.
Com isso, podemos concluir que [tex]MP=MN \, .[/tex]
[tex]\textcolor{#800000}{(5)}[/tex] Vamos agora mostrar que o ângulo [tex]P\hat{M}N[/tex] é um ângulo reto.
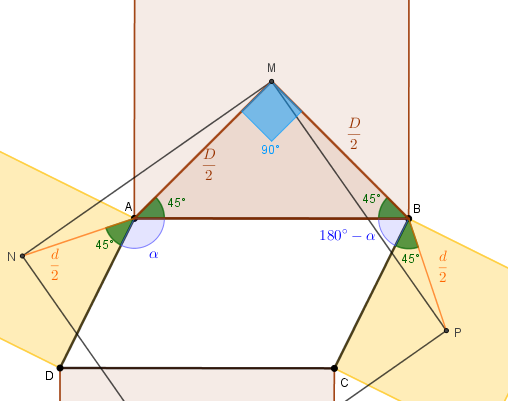
Para tal, observemos inicialmente o triângulo [tex]BMA.[/tex]
Ele é isósceles com os ângulos da base medindo [tex]45^\circ[/tex]. Como a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex], então a medida do ângulo [tex]B\hat{M}A[/tex] é [tex]90^\circ \, .[/tex]
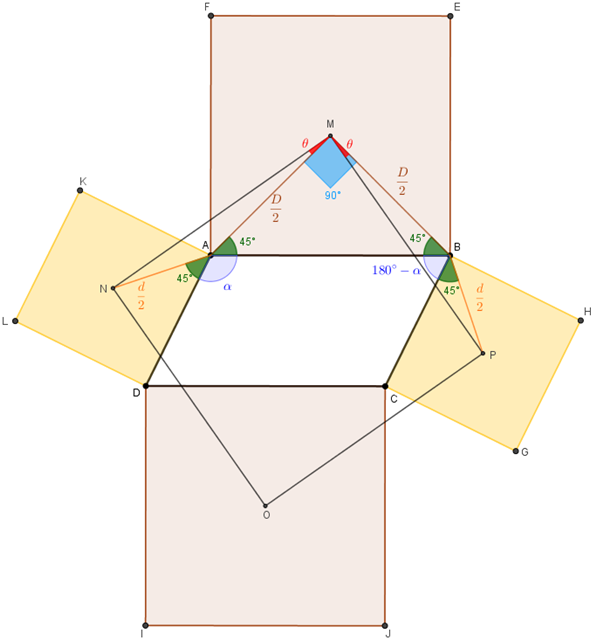
Além disso, pela congruência dos triângulos [tex]MBP[/tex] e [tex]MAN[/tex], temos as medidas dos ângulos [tex]B\hat{M}P[/tex] e [tex]A\hat{M}N[/tex] iguais. Essa medida em graus está representada por [tex]\theta[/tex] na figura abaixo.
Dessa forma, podemos concluir que o ângulo [tex]P\hat{M}N[/tex] é reto, já que sua medida em graus, digamos [tex]\beta[/tex], pode ser assim calculada:
[tex] \qquad \beta=90^{\circ}-\theta+\theta[/tex]
[tex] \qquad \beta=90^{\circ}\cancel{-\theta}\cancel{+\theta}[/tex]
[tex]\qquad \beta=90^{\circ} \, .[/tex]
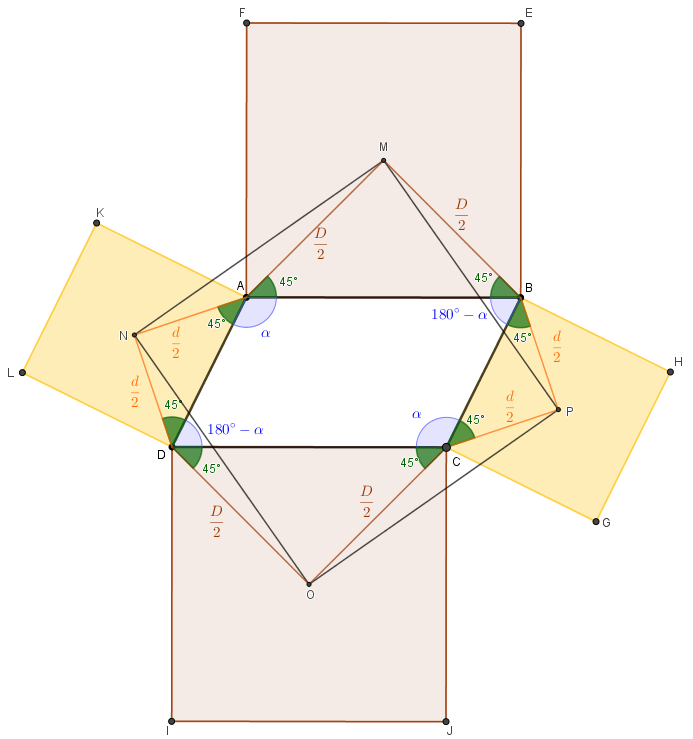
Repetindo a mesma construção geométrica com os outros lados, concluiremos que [tex]MN=NO=OP=PM[/tex] e ainda que os ângulos [tex]M\hat{N}O \, ; \, N\hat{O}P \, [/tex] são retos. (A última figura pode ajudar nas construções.)
Podemos concluir, então, que o quadrilátero [tex]MNOP[/tex] é um quadrado.
Solução elaborada pelos Moderadores do Blog.
