Problema
(Indicado a partir do 9º ano do E. F.)
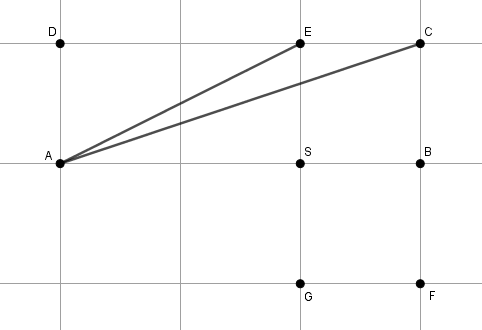
Dois segmentos [tex]\overline{AC}[/tex] e [tex]\overline{AE}[/tex] foram traçados em uma folha de papel quadriculado, como ilustrado na figura abaixo.
Calcule a soma das medidas dos ângulos [tex]B\widehat{A}C[/tex] e [tex]B\widehat{A}E[/tex].

Notações
(I) Denotaremos o segmento de reta definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e seu respectivo comprimento por [tex]XY[/tex].
(II) Denotaremos o ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X [/tex] e [tex]Y[/tex], por [tex]X\widehat{V}Y [/tex] e sua respectiva medida por [tex]mX\widehat{V}Y.[/tex]
Solução 1
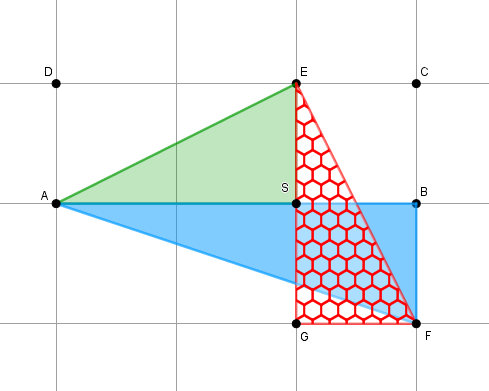
Observando a figura abaixo vemos que [tex]B\widehat{A}C[/tex] e [tex]B\widehat{A}F[/tex] têm medidas iguais, já que o triângulo [tex]CAF[/tex] é isósceles e [tex]B[/tex] é ponto médio de [tex]\overline{CF}[/tex].
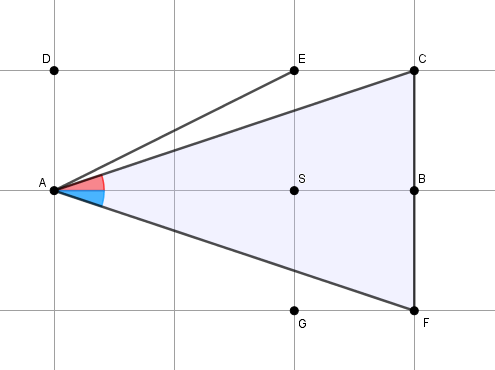
Assim:
[tex]\qquad mB\widehat{A}C+mB\widehat{A}E=mB\widehat{A}F+mB\widehat{A}E=mE\widehat{A}F.\qquad \textcolor{#800000}{(i)}[/tex]
Agora, note que os triângulos [tex]ASE[/tex] e [tex]EGF[/tex] são congruentes (ambos são triângulos retângulos e seus catetos medem 1 e 2 unidades relativas aos lados dos quadradinhos da folha).
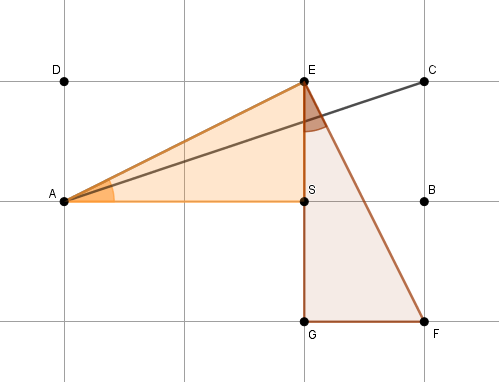
Dessa forma, segue que:
[tex]\qquad mA\widehat{E}F= mA\widehat{E}S+mG\widehat{E}F[/tex]
[tex]\quad\qquad \quad\quad \;=mA\widehat{E}S+mS\widehat{A}E[/tex]
[tex]\quad\qquad \quad\quad \;=180^\circ-mA\widehat{S}E\quad [/tex](Lembre-se de que [tex]mA\widehat{E}S+mS\widehat{A}E+mA\widehat{S}E=180^\circ[/tex].)
[tex]\quad\qquad \quad\quad \;=180^\circ-90^\circ\quad [/tex](Observe que [tex]A\widehat{S}E[/tex] é um ângulo reto.)
[tex]\quad\qquad \quad\quad \;=90^\circ\,. [/tex]
Finalmente, vamos observar o triângulo [tex]AEF[/tex].
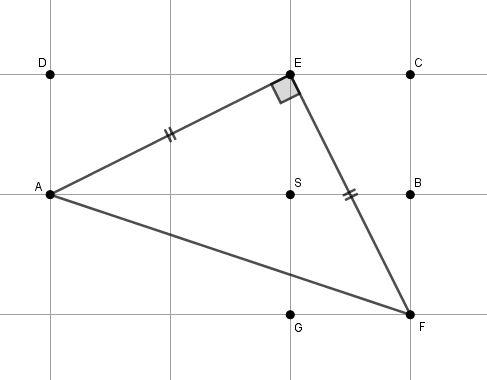
Perceba que
- [tex]AEF[/tex] é um triângulo retângulo isósceles
- [tex]AE=EF\;[/tex]
- [tex]mA\widehat{E}F=90^\circ[/tex];
e, com isso, podemos concluir que [tex]mE\widehat{A}F=45^\circ[/tex]. (Lembre-se de que a soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ[/tex].)
Portanto, segue de [tex]\textcolor{#800000}{(i)}[/tex] que [tex]\,\fcolorbox{black}{#eee0e5}{$\,mB\widehat{A}C+mB\widehat{A}E=45^\circ$}\,[/tex].
Solução elaborada pelos Moderadores do Blog .
Solução 2
Observando a figura a seguir percebemos que [tex]B\widehat AC[/tex] e [tex]B\widehat AF[/tex] têm a mesma medida, pois o triângulo [tex]CAF[/tex] é isósceles e [tex]B[/tex] é o ponto médio de sua base.

Logo,
[tex]\qquad mB\widehat AC+mB\widehat AE= mB\widehat AF+mB\widehat AE=mE\widehat AF. \qquad \textcolor{#800000}{(ii)}[/tex]
Observe, utilizando o Teorema de Pitágoras nos triângulos [tex]AES[/tex], [tex]EGF[/tex] e [tex]ABF[/tex], que [tex]{AE}={EF}=\sqrt5[/tex], enquanto [tex]{AF}=\sqrt{10}[/tex]:
|
Triângulo [tex]AES[/tex]:
[tex]\quad AE^2=AS^2+SE^2\\ \quad AE^2=2^2+1^2\\ \quad AE^2=5\\ \quad \boxed{AE=\sqrt5} .[/tex] |
Triângulo [tex]EGF[/tex]:
[tex]\quad EF^2=EG^2+GF^2\\ \quad EF^2=2^2+1^2\\ \quad EF^2=5\\ \quad \boxed{EF=\sqrt5} .[/tex] |
Triângulo [tex]ABF[/tex]:
[tex]\quad AF^2=AB^2+BF^2\\ \quad AF^2=3^2+1^2\\ \quad AF^2=10\\ \quad \boxed{AF=\sqrt{10}} .[/tex] |
Por outro lado, veja que [tex](\sqrt5)^2+(\sqrt5)^2=(\sqrt{10})^2[/tex], donde conclui-se que o triângulo [tex]AEF[/tex] é retângulo de hipotenusa [tex]\overline{AF}[/tex].
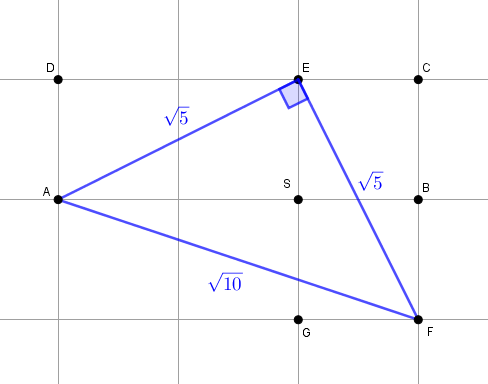
Como o triângulo [tex]AEF[/tex] é também isósceles, pois [tex]{AE}={EF}[/tex], temos que os ângulos [tex]E\widehat FA[/tex] e [tex]E\widehat AF[/tex] são congruentes e a medida desses ângulos é [tex]45^\circ[/tex]. (Lembre-se de que a soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ[/tex].)
Portanto, segue de [tex]\textcolor{#800000}{(ii)}[/tex] que [tex]\,\fcolorbox{black}{#eee0e5}{$\,mB\widehat{A}C+mB\widehat{A}E=45^\circ$}\,[/tex].
Solução elaborada pelos Moderadores do Blog .
