Problema
(Indicado a partir do 9º ano do E. F.)
Um trem saiu do terminal às [tex]6[/tex] horas e chegou à estação de destino no horário marcado no relógio mostrado a seguir.
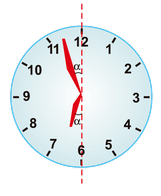
Quanto tempo durou a viagem?

Dicas sobre ponteiros de um relógio
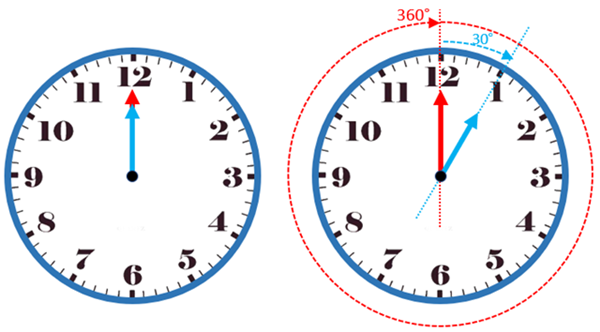
1) Observando com cuidado a figura a seguir, concluímos que, de [tex]12[/tex] horas para [tex]1[/tex] hora:
- o ponteiro dos minutos descreve um ângulo de [tex]360^\circ[/tex];
- o ponteiro das horas descreve um ângulo de [tex]\dfrac{360^\circ}{12}=30^\circ[/tex].
Assim, a razão entre a variação angular dos ponteiros dos minutos e das horas é [tex]\dfrac{360^\circ}{30^\circ}[/tex] ou [tex]\dfrac{12^\circ}{1^\circ}[/tex]. Como ambas as medidas estão em graus, podemos escrever essa razão como [tex]\dfrac{12}{1}[/tex], ou ainda [tex]\boxed{12:1}[/tex] ([tex]12[/tex] para [tex]1[/tex]).
Outra forma de vermos essa razão é observarmos que, no intervalo de uma hora, o ponteiro das horas percorre [tex]1[/tex] grupo de “cinco tracinhos” (que utilizamos para delimitar cinco minutos) e o ponteiro dos minutos percorre [tex]12[/tex] grupos de “cinco tracinhos”.
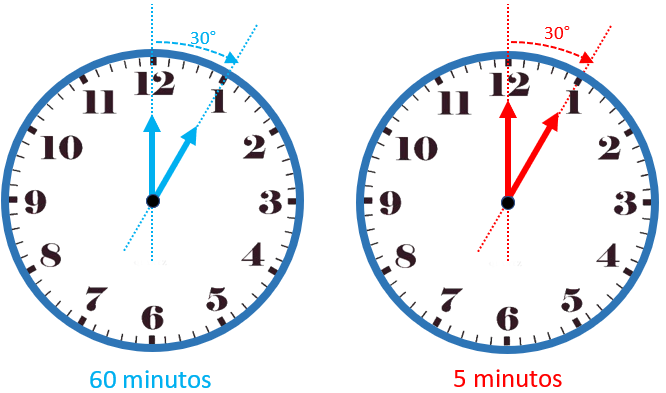
2) Note também que um ângulo de [tex] 30^\circ[/tex] é percorrido em [tex]60[/tex] minutos pelo ponteiro das horas e em apenas [tex]5[/tex] minutos pelo ponteiro dos minutos.
Essas duas observações iniciais vão ajudar bastante na solução deste problema.
Solução 1
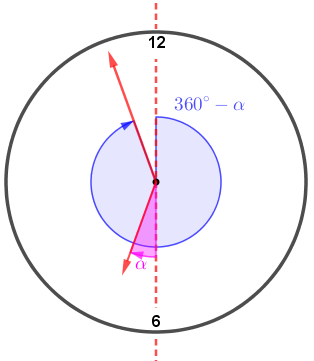
Consideraremos as medidas angulares em graus. Assim, de acordo com a figura do problema, a partir das [tex]6[/tex] horas temos uma variação angular [tex]\alpha[/tex] para o ponteiro das horas e uma variação angular [tex]360^\circ-\alpha[/tex] para o ponteiro dos minutos.
Como a razão entre a variação angular dos ponteiros dos minutos e das horas é [tex]12:1[/tex], segue que:
[tex]\qquad 12\alpha =360^\circ-\alpha \\
\qquad \alpha = \dfrac{360^\circ }{13}\,.[/tex]
Por outro lado, um ângulo de [tex] 30^\circ[/tex] é percorrido em [tex]60[/tex] minutos pelo ponteiro das horas; então uma variação de [tex]1^\circ[/tex] do ponteiro das horas equivale a [tex]2[/tex] minutos no horário marcado pelo ponteiro dos minutos. Deste modo, o tempo [tex]t[/tex] em minutos percorrido pelo trem após as [tex]6[/tex] horas é dado por:
[tex]\qquad t=\dfrac{360^\circ}{13} \cdot \dfrac{2}{1^\circ}\\
\qquad t=\dfrac{720}{13}\\
\qquad t=55\dfrac{5}{13}~min.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Vamos considerar a medida [tex]\alpha[/tex], que aparece na figura do enunciado, tomada em graus.
De acordo com essa mesma figura, a partir das [tex]6[/tex] horas temos uma variação angular [tex]\textcolor{#FF00FF}{~\alpha~}[/tex] para o ponteiro das horas e uma variação angular [tex]\textcolor{#3333FF}{~360^\circ-\alpha~}[/tex] para o ponteiro dos minutos.
Como a razão entre a variação angular dos ponteiros dos minutos e das horas é [tex]\boxed{12:1}[/tex], segue que:
[tex]\quad \quad \dfrac{12}{1}= \dfrac{360^\circ-\alpha}{\alpha}\\
\quad \quad 12\alpha =360^\circ-\alpha \\
\quad \quad 13\alpha =360^\circ \\
\quad \quad \boxed{\alpha = \dfrac{360^\circ}{13}}\,.[/tex]
Portanto, para responder à pergunta do problema, precisamos considerar [tex]\alpha= \dfrac{360^\circ }{13}~[/tex] e
➤ determinar o tempo que o ponteiro das horas levou para percorrer o ângulo de medida [tex]\textcolor{#FF00FF}{~\alpha~}[/tex],
ou
➤ determinar o tempo que o ponteiro dos minutos levou para percorrer o ângulo de medida [tex]\textcolor{#3333FF}{~360^\circ-\alpha~}[/tex].
Vamos fazer os dois procedimentos!
- Ponteiro das horas:
Como o ponteiro das horas leva [tex]60[/tex] minutos para percorrer um ângulo de [tex]30^\circ[/tex], podemos determinar o tempo que o ponteiro das horas levou para percorrer o ângulo de medida
[tex]\qquad\boxed{\textcolor{#FF00FF}{ \alpha=\dfrac{360^\circ }{13}}}[/tex]
com a ajuda de uma regrinha de três simples.
[tex]~~\\
\qquad \qquad \begin{array}{c c c}
\; 60~minutos & \text{————–} & 30^\circ \\
\; x~ minutos & \text{————–} & \textcolor{#FF00FF}{\dfrac{360^\circ }{13}} \end{array}[/tex]
Vejamos:
[tex]\qquad 30^\circ\cdot x=60\cdot \dfrac{360^\circ}{13}\\
\qquad \cancel{30^\circ}\cdot x=60\cdot \dfrac{\cancel{30^\circ}\cdot 12}{13}\\
\qquad x=60\cdot \dfrac{12}{13}\\
\qquad x=\dfrac{720}{13}\\
\qquad x=55+\dfrac{5}{13}=55\frac{5}{13}~min\,.[/tex] - Ponteiro dos minutos:
Como o ponteiro dos minutos leva [tex]5[/tex] minutos para percorrer um ângulo de [tex] 30^\circ[/tex], podemos determinar o tempo que o ponteiro dos minutos levou para percorrer o ângulo de medida
[tex]\qquad\boxed{\textcolor{#3333FF}{ 360^\circ-\alpha= 360^\circ-\dfrac{360^\circ}{13}=\dfrac{12\cdot360^\circ }{13}}}[/tex]
com a ajuda desta regrinha de três simples:
[tex]~~\\
\qquad \qquad \begin{array}{c c c}
\; 5~minutos & \text{————–} & 30^\circ \\
\; x~ minutos & \text{————–} & \textcolor{#3333FF}{\dfrac{12\cdot360^\circ}{13}}\,. \end{array}[/tex]
Assim:
[tex]\qquad 30^\circ\cdot x=5\cdot \dfrac{12\cdot360^\circ }{13} \\
\qquad \cancel{30^\circ}\cdot x=5\cdot \dfrac{12\cdot\cancel{30^\circ}\cdot 12}{13} \\
\qquad x=5\cdot \dfrac{12\cdot 12}{13}\\
\qquad x=\dfrac{720}{13}\\
\qquad x=55+\dfrac{5}{13}=55\frac{5}{13}~min\,.[/tex]
Pelo exposto, o tempo gasto pelo trem após as [tex]6[/tex] horas foi de [tex]~55\frac{5}{13}~min[/tex] e, portanto, a viagem durou pouco mais de [tex]55[/tex] minutos.
Solução elaborada pelos Moderadores do Blog.
