Problema
(Indicado a partir do 9º ano do E. F.)
Na figura abaixo, os pontos [tex]A[/tex] , [tex]B[/tex] e [tex]C[/tex] definem um triângulo.
Observe que [tex]M[/tex] é o ponto médio do lado [tex]\overline{BC}[/tex], [tex]\overline{AN}[/tex] é a bissetriz do ângulo [tex]B\hat{A}C[/tex] e [tex]\overline{BN}[/tex] é perpendicular a [tex]\overline{AN}[/tex].
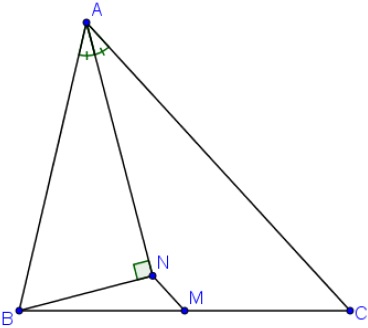
Sabendo que [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] medem respectivamente [tex]14 \, m[/tex] e [tex]19 \, m[/tex], calcule o comprimento do segmento [tex]\overline{MN}.[/tex]

Lembretes
Propriedade: Dado um triângulo, a base média com extremos nos pontos médios de dois lados desse triângulo é paralela ao terceiro lado e a sua medida é igual à metade da medida desse terceiro lado.
(Se você não sabe o que é uma base média de um triângulo, clique AQUI).
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].
Solução
A partir da figura dada no problema, seja [tex]D[/tex] o ponto de interseção do prolongamento do segmento [tex]\overline{BN}[/tex] com o lado [tex]\overline{AC}[/tex].
Perceba que os triângulos [tex]ANB \, [/tex] e [tex] \, AND[/tex] são congruentes (caso [tex]A.L.A.[/tex]: ângulo – lado – ângulo).
Com isso, concluímos que o triângulo [tex]ABD[/tex] é isósceles, já que [tex]AB=AD[/tex].
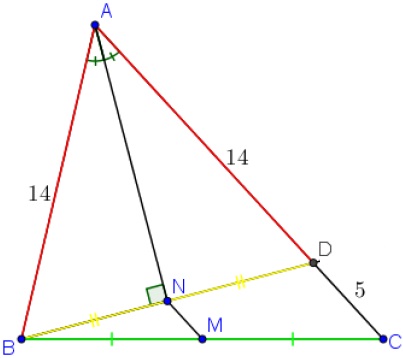
Como [tex]\overline{BN}[/tex] é perpendicular a [tex]\overline{AN}[/tex] e o triângulo [tex]ABD[/tex] é isósceles, então [tex]N[/tex] é ponto médio de [tex]\overline{BD}[/tex]. Portanto, o segmento [tex]\overline{MN}[/tex] é uma base média do triângulo [tex]BDC[/tex].
Dessa forma, pela propriedade citada nos Lembretes, [tex] \, \fcolorbox{black}{#eee0e5}{$MN=\dfrac{5}{2}=2,5 \, m$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
