Problema
(Indicado a partir do 9º ano do E. F.)
(Adaptado – Projeto de Extensão – UFGD- CAPACITAÇÃO PARA PROFESSORES DA REDE PÚBLICA) Calcule a medida do segmento [tex]AB[/tex] da figura, que é formada por quatro quadrados cujos lados medem [tex]4\, cm[/tex], sendo que [tex]A_{1}[/tex], [tex]A_{2}[/tex] e [tex]A_{3}[/tex] são pontos médios dos segmentos [tex] B_{1}C_{1}[/tex], [tex]B_{2}C_{2}[/tex] e [tex]B_{3}C_{3}[/tex], respectivamente.
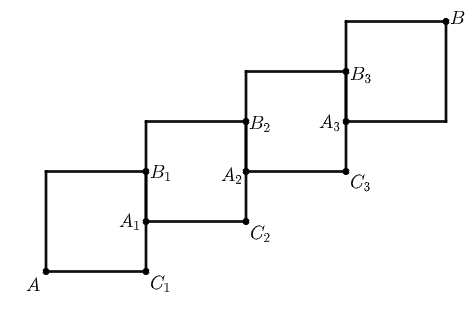
Solução
Considere na figura abaixo o triângulo [tex]ABC.[/tex]
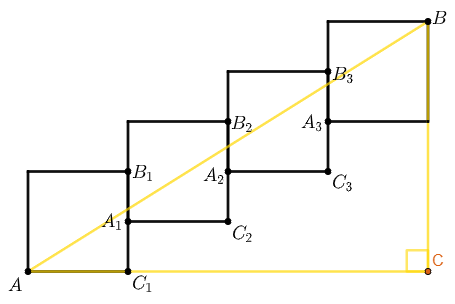
Para calcular a medida do segmento [tex]AB[/tex], aplicaremos o Teorema de Pitágoras no triângulo [tex]ABC[/tex]. Para isso, observe que:
- A medida de [tex]AC[/tex] é igual à soma das medidas dos segmentos [tex]AC_{1},\, C_{1}C_{2}’\,[/tex], [tex]C’_{2}C_{3}'[/tex] e [tex]C_{3}’C[/tex], indicados na figura abaixo. Assim, o segmento [tex]AC[/tex] mede [tex]4 \times 4\, cm=16\, cm.[/tex]
- Por outro lado, a medida do segmento [tex]BC[/tex] é duas vezes a medida do lado de um dos quadrados mais a metade da medida do lado de um desses quadrados, ou seja, [tex]10\,.[/tex]
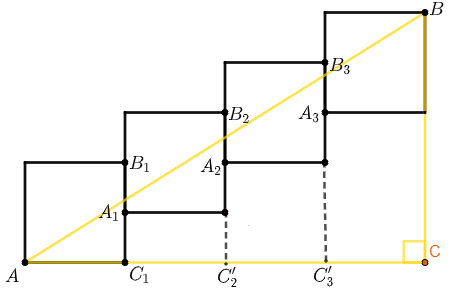
Dessa forma, se [tex]x[/tex] é a medida em centímetros do segmento [tex]AB[/tex], segue do Teorema de Pitágoras que:
[tex]\qquad x^{2}=16^{2}+10^{2}=256+100=356=4\cdot 89[/tex].
Logo, como [tex] x[/tex] é positivo, [tex]\, \fcolorbox{black}{#eee0e5}{$x=2 \sqrt{89}\,cm$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
