Problema
(Indicado a partir do 9º ano do E. F.)
Sejam [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] as medidas, em centímetros, da hipotenusa e dos catetos de um triângulo retângulo, respectivamente.
O que podemos afirmar sobre os valores das raízes da equação [tex]\boxed{a^2 x^2 – b^2 x – c^2 = 0}[/tex] ?
Lembrete
Existem importantes relações entre os coeficientes de uma equação do segundo grau e suas raízes. Se você não se lembra dessas relações, consulte o seguinte texto do nosso Blog: Relações de Girard.
Solução
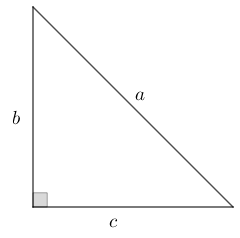Considere um triângulo retângulo cuja hipotenusa e os dois catetos meçam [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] centímetros, conforme mostra a figura ao lado.Do teorema de Pitágoras, temos [tex]a^2=b^2+c^2[/tex]; assim, segue que:
[tex]\qquad a^2=b^2+c^2[/tex]
[tex]\qquad a^2-b^2-c^2 = 0[/tex]
[tex]\qquad a^2\cdot 1^2 – b^2\cdot 1 – c^2 = 0. \qquad \textcolor{#800000}{(i)}[/tex]
- Observe que a igualdade [tex]\textcolor{#800000}{(i)}[/tex] nos permite concluir que uma das raízes da equação [tex]\boxed{a^2 x^2 – b^2 x – c^2 = 0} \, [/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$1$} \, [/tex], já que [tex] \boxed{a^2\cdot \boxed{1}^2 – b^2\cdot \boxed{1} – c^2 = 0}.[/tex]
- Por outro lado, da relação entre o produto de raízes e coeficientes (segunda Relação de Girard no texto indicado), temos que o produto das duas raízes da nossa equação é [tex]- \dfrac{c^2}{a^2}[/tex].
Se uma das raízes é [tex]1[/tex] e o produto das duas raízes da nossa equação é [tex]- \dfrac{c^2}{a^2}[/tex], então a outra raiz é [tex]\fcolorbox{black}{#eee0e5}{$- \dfrac{c^2}{a^2}$}[/tex].
Mas observe que, como [tex]c[/tex] é um cateto e [tex]a[/tex] é a hipotenusa do triângulo retângulo em questão, então [tex]0 \lt c \lt a[/tex] e assim:
[tex]\qquad \begin{cases}
0 \lt c^2 \lt c\cdot a\\
0 \lt a \cdot c \lt a^2
\end{cases} \, [/tex].
Portanto, [tex]0 \lt c^2 \lt c\cdot a = a \cdot c \lt a^2 [/tex], donde:
[tex]\qquad 0 \lt c^2 \lt a^2 \, [/tex]
[tex]\qquad 0 \lt \dfrac{c^2}{ a^2} \lt 1 \, [/tex]
[tex]\qquad 0 \gt -\dfrac{c^2}{ a^2} \gt -1 \, [/tex]
[tex]\qquad -1 \lt -\dfrac{c^2}{ a^2} \lt 0 \, [/tex].
Assim, uma das raízes da equação é [tex]1[/tex] e a segunda raiz é um número real entre [tex]-1[/tex] e [tex]0[/tex].
Solução elaborada pelos Moderadores do Blog.