Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Difícil)
Seis triângulos foram desenhados e coloridos conforme mostra a figura abaixo.
Distribua os números [tex]0, 1, 2, 3, 4, 5, 6, 7, 8[/tex] e [tex]9[/tex] nos círculos que foram colocados sobre os vértices dos triângulos, de modo que as somas dos números colocados nos três vértices de cada triângulo colorido sejam iguais.
De quantas maneiras é possível fazer essa distribuição?
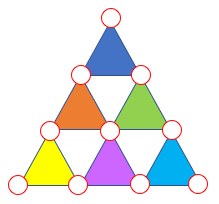
Observação: Para fazer a distribuição, considere os triângulos fixos e, portanto, não faça rotações ou simetrias.
Extraído da OBM Sênior, 1994.
Solução
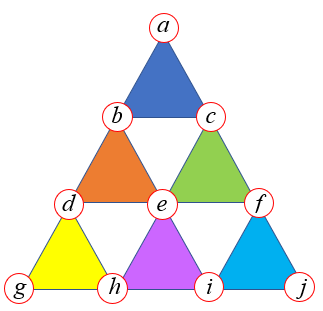
Sejam [tex]a,b,c,d,e,f,g,h,i,j[/tex] os números colocados nos vértices, conforme ilustra a próxima figura.
Como [tex]a,b,c,d,e,f,g,h,i[/tex] e [tex]j[/tex] são números distintos que valem [tex]0,1,\cdots,8,9[/tex], temos que:
[tex]\qquad a+b+c+d+e+f+g+h+i+j=0+1+\cdots+8+9=45\,.[/tex]
Sabemos que as somas dos números colocados nos três vértices de cada um dos seis triângulos coloridos são iguais; assim, temos também:
[tex]\qquad \textcolor{#345da8}{a+b+c=S}[/tex]
[tex]\qquad \textcolor{#e86a14}{b+d+e=S}[/tex]
[tex]\qquad \textcolor{#92D050}{c+e+f=S}[/tex]
[tex]\qquad \textcolor{#dd0}{d+g+h=S}[/tex]
[tex]\qquad \textcolor{#CC66FF}{e+h+i=S}[/tex]
[tex]\qquad \textcolor{#00B0F0}{f+i+j=S}[/tex].
Observe que na primeira, na quarta e na sexta igualdades não aparece o número [tex]e[/tex]; assim, somando essas três igualdades segue que:
[tex]\qquad (a+b+c)+(d+g+h)+(f+i+j)=3S\\
\qquad a+b+c+d+f+g+h+i+j=3S\\
\qquad 45-e=3S\\
\qquad e=45-3S\\
\qquad e=3\cdot(15-S)\,. \quad \textcolor{#800000}{(i)}[/tex]
Como [tex]15-S[/tex] é um número inteiro, a igualdade [tex]\textcolor{#800000}{(i)}[/tex] nos mostra que [tex]e[/tex] é um múltiplo de [tex]3[/tex]. Assim, temos apenas quatro opções para o número [tex]e[/tex]: [tex]0[/tex], [tex]3[/tex], [tex]6[/tex] ou [tex]9[/tex] .
Mas por outro lado, o número [tex]e[/tex] aparece em vértices de três triângulos; assim, devem existir números naturais [tex]b,d,c,f,h,i[/tex] tais que
[tex]\qquad \qquad \boxed{b+d=S-e}\quad[/tex] ; [tex]\qquad \boxed{c+f=S-e}\quad[/tex] ; [tex]\qquad \boxed{h+i=S-e}[/tex].
Vamos, então, testar os quatro valores possíveis de [tex]e[/tex], observando que a diferença [tex]S-e[/tex] deverá ser escrita de três maneiras diferentes, a partir dos algarismos [tex]0, 1, 2, 3, 4, 5, 6, 7, 8,9[/tex].
- Se [tex]e=0[/tex], de [tex]\textcolor{#800000}{(i)}[/tex] concluímos que [tex]S=15[/tex] e, portanto, [tex]S-e=15[/tex]. Mas perceba que [tex]15[/tex] só pode ser escrito como [tex]6+9[/tex] e [tex]7+8[/tex]; logo, [tex]e[/tex] não pode ser [tex]0\,.[/tex]
- Se [tex]e=3[/tex], de [tex]\textcolor{#800000}{(i)}[/tex] concluímos que [tex]S=14[/tex] e, portanto, [tex]S-e=11[/tex]. Perceba que [tex]2+9=11[/tex], [tex]4+7=11[/tex] e [tex]5+6=11[/tex]; logo, [tex]e[/tex] pode ser [tex]3\,.[/tex]
- Se [tex]e=6[/tex], de [tex]\textcolor{#800000}{(i)}[/tex] concluímos que [tex]S=13[/tex] e, portanto, [tex]S-e=7[/tex]. Perceba que [tex]0+7=7[/tex], [tex]2+5=7[/tex] e [tex]3+4=7[/tex]; logo, [tex]e[/tex] pode ser [tex]6\,.[/tex]
- Se [tex]e=9[/tex], de [tex]\textcolor{#800000}{(i)}[/tex] concluímos que [tex]S=12[/tex] e, portanto, [tex]S-e=3[/tex]. Mas perceba que [tex]3[/tex] só pode ser escrito como [tex]0+3[/tex] e [tex]1+2[/tex]; logo, [tex]e[/tex] não pode ser [tex]9\,.[/tex]
Temos, então, duas soluções para o problema, a menos de rotações ou simetrias:
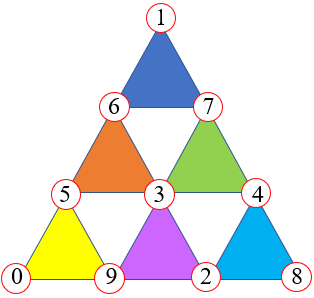
- Para [tex]e=3[/tex], uma das configurações é mostrada a seguir.
- Para [tex]e=6[/tex], mostramos, a seguir, uma das configurações possíveis.
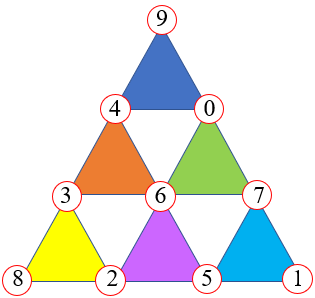
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
