✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
(UK Junior Mathematical Olympiad 2012 – Adaptado) No triângulo [tex]ABC[/tex] da figura:
- [tex]D[/tex] é um ponto do segmento [tex]AB [/tex] tal que os segmentos [tex]AD[/tex] e [tex]DC[/tex] têm o mesmo comprimento;
- a medida do ângulo [tex]A\hat BC[/tex] é [tex]72^\circ[/tex];
- a medida do ângulo [tex]A \hat DC [/tex] é cinco vezes a medida de [tex]D \hat CB[/tex].
Qual a medida do ângulo [tex]A \hat CD[/tex]?
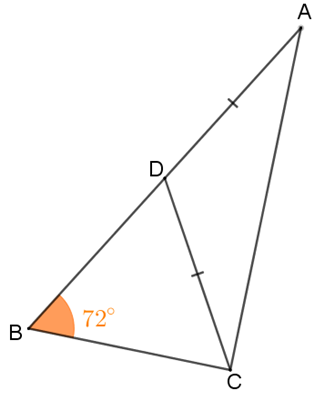 Observação: Figura não proporcional aos dados do problema.
Observação: Figura não proporcional aos dados do problema.
Solução
Seja [tex]\alpha[/tex] a medida em graus do ângulo [tex] D \hat C B.[/tex] Assim, a medida em graus do ângulo [tex] A \hat DC[/tex] é [tex]5\alpha[/tex] e, consequentemente, a medida de [tex] C \hat DB[/tex] é [tex]180^\circ-5\alpha[/tex], já que [tex] A \hat DC[/tex] e [tex] C \hat DB[/tex] são ângulos suplementares.
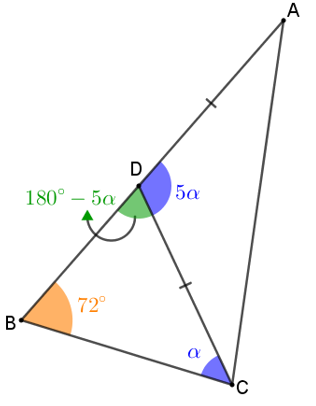
Como a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ [/tex], observando o triângulo [tex]BDC[/tex] segue que
[tex]\qquad \left(180^\circ-5\alpha \right)+\alpha+72^\circ=180^\circ [/tex]
[tex]\qquad \cancel{180^\circ}-5\alpha +\alpha+72^\circ=\cancel{180^\circ} [/tex]
[tex]\qquad 4\alpha =72^\circ [/tex]
[tex]\qquad \alpha =18^\circ .[/tex]
A partir da medida [tex]\alpha[/tex], obtemos que a medida do ângulo [tex] A \hat D C[/tex] é [tex]5 \times 18^\circ= 90^\circ.[/tex]
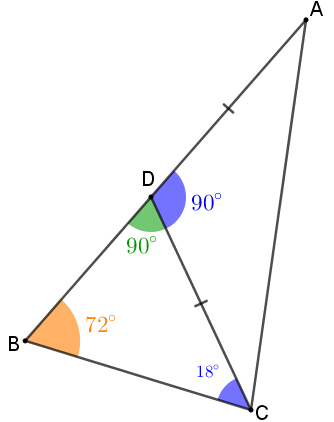
Finalmente, já podemos calcular a medida do ângulo [tex]A \hat CD[/tex].
Note que [tex]A \hat CD[/tex] é um dos ângulos da base de um triângulo isósceles; assim, se sua medida em graus for denotada por [tex]x[/tex], então a medida do ângulo [tex]D \hat A C[/tex] também será [tex]x[/tex]. Com isso, utilizando mais uma vez que "a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ [/tex]" segue que:
[tex]\qquad x+90^\circ +x=180^\circ [/tex]
[tex]\qquad 2x+90^\circ =180^\circ [/tex]
[tex]\qquad 2x =90^\circ [/tex]
[tex]\qquad x =45^\circ .[/tex]
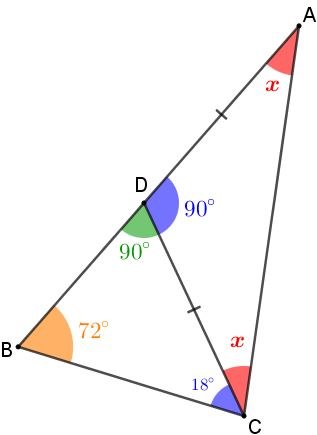
Pelo exposto, a medida do ângulo [tex] A \hat C D[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$45^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
