✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Médio)
De cada [tex]10[/tex] clientes que Leandro atende na loja onde trabalha, ele consegue efetivar a venda para [tex]3.[/tex]
Levando-se em consideração que a decisão de compra ou não de um cliente não influencia na decisão de outro, qual a probabilidade de que Leandro consiga efetivar pelo menos uma venda em quatro atendimentos?
Solução 1
Inicialmente, observe que, como de cada [tex]10[/tex] clientes que Leandro atende, ele consegue efetivar a venda para [tex]3[/tex], a probabilidade de uma venda ser efetuada é [tex]\dfrac{3}{10}[/tex] ou [tex]0,3[/tex] e, consequentemente, a probabilidade de uma venda NÃO ser efetuada é [tex]\dfrac{7}{10}[/tex] ou [tex]0,7.[/tex]
Em seguida, vamos tentar entender o que significa o Leandro efetivar "pelo menos uma venda em quatro atendimentos". Para isso, suponha que ele vá atender aos clientes A, B, C e D.
Se o Leandro tem que efetivar pelo menos uma venda com relação ao atendimento desses quatro clientes, isso significa que ele pode efetivar exatamente uma venda, ou exatamente duas vendas, ou exatamente três vendas, ou exatamente quatro vendas.
- Efetivar exatamente uma venda no atendimento aos clientes A, B, C e D, por sua vez, significa uma e somente uma das seguintes situações:
- A comprou e os demais não compraram;
- B comprou e os demais não compraram;
- C comprou e os demais não compraram;
- D comprou e os demais não compraram.
- Efetivar exatamente duas vendas no atendimento aos clientes A, B, C e D, por sua vez, significa uma e somente uma das seguintes situações:
- "A e B compraram" e "C e D não compraram";
- "A e C compraram" e "B e D não compraram";
- "A e D compraram" e "B e C não compraram";
- "B e C compraram" e "A e D não compraram";
- "B e D compraram" e "A e C não compraram";
- "C e D compraram" e "A e B não compraram".
- Efetivar exatamente três vendas no atendimento aos clientes A, B, C e D, por sua vez, significa uma e somente uma das seguintes situações:
- "A e B e C compraram" e "D não comprou";
- "A e B e D compraram" e "C não comprou";
- "A e C e D compraram" e "B não comprou";
- "B e C e D compraram" e "A não comprou".
- Finalmente, efetivar exatamente quatro vendas no atendimento aos clientes A, B, C e D, significa que:
- "A e B e C e D compraram"
Assim, a probabilidade de apenas uma venda ser efetivada é dada por:
[tex]P_1=\left[\dfrac{3}{10}\textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{7}{10}\right]+
\left[\dfrac{7}{10}\textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{7}{10}\right]+\\
\quad+\left[\dfrac{7}{10}\textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{7}{10}\right] +\left[\dfrac{7}{10}\textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{3}{10}\right][/tex]
[tex]P_1=4 \times \left[\dfrac{3}{10}\times \left(\dfrac{7}{10}\right)^3 \right][/tex]
[tex]\boxed{P_1=0,4116}.[/tex]
Assim, a probabilidade de apenas duas vendas serem efetivadas é dada por:
[tex]P_2=\left[\dfrac{3}{10}\textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{7}{10}\right]+\left[\dfrac{3}{10}\textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{7}{10}\right]+\\
\qquad + \left[\dfrac{3}{10}\textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{3}{10}\right]
+\left[\dfrac{7}{10}\textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{7}{10}\right]+\\
\qquad +\left[\dfrac{7}{10}\textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{3}{10}\right]+\left[\dfrac{7}{10}\textcolor{red}{ \times} \dfrac{7}{10}\textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{3}{10}\right][/tex]
[tex]P_2=6 \times \left[\left(\dfrac{3}{10}\right)^2\times \left(\dfrac{7}{10}\right)^2 \right][/tex]
[tex]\boxed{P_2=0,2646}.[/tex]
Assim, a probabilidade de apenas três vendas serem efetivadas é dada por:
[tex]P_3=\left[\dfrac{3}{10}\textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{7}{10}\right]+\left[\dfrac{3}{10}\textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{3}{10}\right]+\\
\qquad + \left[\dfrac{3}{10}\textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{3}{10}\right]+
\left[\dfrac{7}{10}\textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{3}{10}\right][/tex]
[tex]P_3=4 \times \left[\left(\dfrac{3}{10}\right)^3\times \dfrac{7}{10} \right][/tex]
[tex]\boxed{P_3=0,0756}.[/tex]
e a probabilidade de isso ocorrer é dada por:
[tex]P_4=\dfrac{3}{10}\textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{3}{10} \textcolor{red}{ \times} \dfrac{3}{10}[/tex]
[tex]P_4=\left(\dfrac{3}{10}\right)^4[/tex]
[tex]\boxed{P_4=0,0081}.[/tex]
Agora que já temos as probabilidades de serem efetivas exatamente uma, exatamente duas, exatamente três vendas e exatamente quatro vendas, vamos calcular a probabilidade final que é a de Leandro conseguir efetivar "exatamente uma venda" ou "exatamente duas vendas", ou "exatamente três vendas", ou "exatamente quatro vendas":
[tex]\qquad P=0,4116\textcolor{blue}{+}0,2646\textcolor{blue}{+}0,0756\textcolor{blue}{+}0,0081[/tex]
[tex]\qquad \boxed{P=0,7599} \, .[/tex]
Veja o esqueminha abaixo.
[tex] \begin{array}{|c c c c |}
\hline
\boxed{\text{exatamente 1 }}& \textcolor{blue}{\text{ou}}&\boxed{\text{exatamente 2}}&\textcolor{blue}{\text{ou}}& \boxed{\text{exatamente 3}}& \textcolor{blue}{\text{ou}}&\boxed{\text{exatamente 4}}\\
0,4116 &\textcolor{blue}{ +} & 0,2646 &\textcolor{blue}{+}& 0,0756 &\textcolor{blue}{+} &0,0081\\
\hline
\end{array}[/tex]
Portanto, a probabilidade de que Leandro consiga efetivar pelo menos uma venda em quatro atendimentos é [tex] \, \fcolorbox{black}{#eee0e5}{$0,7599$} \, [/tex], ou aproximadamente [tex] \, \fcolorbox{black}{#eee0e5}{$76\%$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Poderíamos ter poupado todos esses cálculos se tivéssemos utilizado a chamada "probabilidade complementar".
O que é isso? – Veja a AJUDA abaixo. |
AJUDA
Sabemos que um evento [tex]E[/tex] pode ocorrer ou não. Se o evento [tex]E[/tex] for relativo a um espaço amostral [tex] \, \Omega[/tex], o evento associado à não ocorrência de [tex]E[/tex] é denominado o complementar de [tex]E[/tex] com relação a [tex] \, \Omega[/tex] e é denotado por [tex]\overline{E}[/tex].
- Logo, [tex]\overline{E}[/tex] ocorre se, e somente se, [tex]E[/tex] não ocorrer.
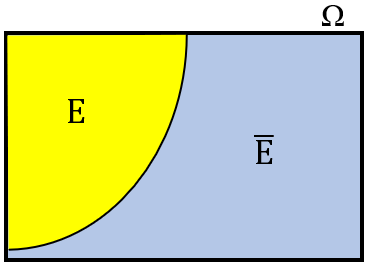
Dessa forma, se [tex]P[/tex] for a probabilidade de que o evento [tex]E[/tex] ocorra (sucesso) e [tex]Q[/tex] for a probabilidade de que [tex]E[/tex] não ocorra (insucesso), então [tex]Q[/tex] é a probabilidade do evento complementar [tex]\overline{E}[/tex], ou simplesmente probabilidade complementar de [tex]P[/tex], e temos a seguinte relação: [tex]\boxed{P+Q=1} \, .[/tex]
Solução 2
No caso específico do nosso problema, o evento [tex]E[/tex] é o Leandro "efetivar pelo menos uma venda no espaço amostral formado pelos quatro clientes A, B, C e D" e o evento [tex]\overline{E}[/tex] é o Leandro "NÃO efetivar pelo menos uma venda no espaço amostral formado pelos quatro clientes A, B, C e D", ou seja, o Leandro "efetivar [tex]0[/tex] vendas". Então [tex]P[/tex] é a probabilidade que queremos e [tex]Q[/tex] é a probabilidade que vamos calcular.
Leandro ter efetivado [tex]0[/tex] vendas significa que ele "não efetivou a venda para o cliente A" e "não efetivou a venda para o cliente B" e "não efetivou a venda para o cliente C" e "não efetivou a venda para o cliente D".
Como de cada [tex]10[/tex] clientes que Leandro atende ele consegue efetivar a venda para [tex]3[/tex], a probabilidade de uma venda ser efetuada é [tex]\dfrac{3}{10}[/tex] ou [tex]0,3[/tex] e, consequentemente, a probabilidade de uma venda NÃO ser efetuada é [tex]\dfrac{7}{10}[/tex] ou [tex]0,7[/tex]. Assim, como os eventos são independentes, segue que:
[tex]\qquad Q=\dfrac{7}{10} \textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{7}{10} \textcolor{red}{ \times} \dfrac{7}{10} [/tex]
[tex]\qquad Q=\left(\dfrac{7}{10} \right)^4 [/tex]
[tex]\qquad Q=0,2401. [/tex]
Portanto, a probabilidade [tex]P[/tex] de que Leandro consiga efetivar pelo menos uma venda em quatro atendimentos é dada por:
[tex]\qquad P=1-Q\\
\qquad P=1-0,2401\\
\qquad P= \, \fcolorbox{black}{#eee0e5}{$0,7599$} \, ,[/tex]
ou seja, [tex] \, \fcolorbox{black}{#eee0e5}{$76\%$} \,[/tex], aproximadamente.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
