✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M.) (Nível: Difícil)
(OPM 2004 – adaptado) Um grupo de colegas resolveu construir torres utilizando cartas de baralho.
Construíram inicialmente torres com um, dois, três e cinco andares, como as indicadas na figura.
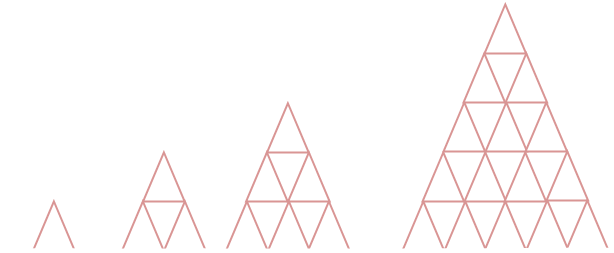
Quantas cartas serão necessárias para que eles construam uma torre do mesmo tipo, só que com cem andares?

Lembrete
✐ A soma dos [tex]n[/tex] primeiros números naturais não nulos é dada por [tex] \boxed{1+2+3+ \cdots+n=\dfrac{(1+n)\cdot n}{2}}[/tex].
(Para aprender um pouco mais sobre a soma [tex]1+2+3+ \cdots+n[/tex], clique AQUI)
Solução
Note que:
- Para o primeiro andar, serão necessárias apenas [tex]2[/tex] cartas.
- Para o segundo andar, o grupo de colegas precisará de uma carta na horizontal, para apoiar as cartas do primeiro andar, e de [tex]2+2[/tex] cartas para a montagem do segundo andar propriamente dito.
- Para o terceiro andar, o grupo precisará de duas cartas na horizontal, para apoiar as cartas do segundo andar, e de [tex]2+2+2[/tex] cartas para a montagem do terceiro andar propriamente dito.
- Para o quarto andar, serão necessárias três cartas na horizontal, para apoiar as cartas do terceiro andar, e [tex]2+2+2+2[/tex] cartas para a montagem do quarto andar propriamente dito.
- Para o quinto andar, serão necessárias quatro cartas na horizontal, para apoiar as cartas do quarto andar, e [tex]2+2+2+2+2[/tex] cartas para a montagem do quinto andar propriamente dito.
- E assim por diante…
Com a tabela abaixo, podemos observar a quantidade de cartas a serem utilizadas, por andar, na construção da torre.
| Andar | Número de cartas por andar |
| 1° andar | [tex][0]+[1\times 2][/tex] |
| 2° andar | [tex] [1] + [2\times 2] [/tex] |
| 3° andar | [tex] [2] + [3\times 2][/tex] |
| 4° andar | [tex] [3] + [4\times 2][/tex] |
| 5° andar | [tex][4] + [5\times 2][/tex] |
| [tex] \cdots[/tex] | |
| n° andar | [tex][n-1] + [n\times 2][/tex] |
| [tex] \cdots[/tex] | |
| 100° andar | [tex][99] + [100\times 2][/tex] |
Para obter a quantidade [tex]Q[/tex] de cartas necessárias para a construção da torre de cem andares, devemos somar a quantidade de cartas que serão utilizadas em cada andar.
Observe:
[tex]\quad Q=\left([0]+[1\times 2]\right) +\left([1] + [2\times 2] \right)+\left([2] + [3\times 2]\right)+\left([3] + [4\times 2]\right)+\\
\quad \quad\quad +\left([4]+[5\times 2]\right) +\cdots+\left([99] + [100\times 2]\right)[/tex]
[tex]\quad Q= (0+1+2+3+4+\cdots+99)+\\
\quad \quad\quad +(1 \times 2+2 \times 2+3 \times 2+4 \times 2+5 \times 2+ \cdots+100 \times 2)[/tex]
[tex]\quad Q= (1+2+3+4+\cdots+99)+2 \times(1 +2 +3 +4 +5+ \cdots+100)[/tex]
[tex]\quad Q= (1+2+3+4+\cdots+99)+2 \times(1 +2 +3 +4 +5+ \cdots+99+100)[/tex]
[tex]\quad Q= (1+2+3+4+\cdots+99)+2 \times(1 +2 +3 +4 +5+ \cdots+99) +2 \times 100[/tex]
[tex]\quad Q= 3 \times (1+2+3+4+\cdots+99)+200[/tex].
Utilizando a fórmula do Lembrete, temos que
[tex] \quad 1+2+3+4+ \cdots+99=\dfrac{100\times 99}{2}=50 \times 99=4950[/tex],
assim,
[tex]\quad \, \fcolorbox{black}{#eee0e5}{$Q= 3 \times 4950+200=15050$} \, [/tex].
Portanto, serão necessárias [tex]15\ 050[/tex] cartas para que o grupo de colegas consiga montar a torre com [tex]100[/tex] andares.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
