✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)
(ONEM – 2008) Foram escritos em uma folha de papel, em ordem crescente, os primeiros três mil números inteiros positivos que são múltiplos de [tex]2[/tex] ou de [tex]3[/tex], mas não múltiplos de ambos.
Nessa sequência, que número ocupa a posição [tex]2018[/tex]?

Ajuda
Algoritmo de Euclides ou Algoritmo da Divisão
Sejam [tex]a[/tex] e [tex]b[/tex] números naturais, com [tex]b\ne 0.[/tex]
|
[tex]\qquad \qquad \begin{array}{r} a \, \end{array} \begin{array}{|r} \, b \, \, \, \\ \hline \end{array}[/tex] [tex]\qquad \qquad\begin{array}{r} r \end{array}\begin{array}{r} \, \, \, q \end{array}\qquad \qquad[/tex] |
Ao dividirmos [tex]a[/tex] por [tex]b[/tex] encontraremos um quociente [tex]q [/tex] e um resto [tex]r [/tex], naturais e únicos, tais que: [tex] \, \, \, \\(1) \, \, \, \, \, \, 0 \le r \lt b \, \, \, \, \, \, \, (2) \, \, a=q \, b+r.[/tex] |
Solução
Vamos fazer algumas considerações, antes de resolvermos o problema propriamente dito.
Sem muito formalismo, ao dividirmos um número natural [tex]n [/tex] por seis podemos encontrar resto [tex]0, \, 1, \, 2, \, 3, \, 4 [/tex] ou [tex]5[/tex].
- Se [tex]n [/tex] deixa resto [tex]0[/tex], então [tex]n [/tex] é múltiplo de [tex]2[/tex] e de [tex]3[/tex] simultaneamente.
- Se [tex]n [/tex] deixa resto [tex]1[/tex], então [tex]n [/tex] não é múltiplo de [tex]2[/tex] e nem [tex]3[/tex].
- Se [tex]n [/tex] deixa resto [tex]2[/tex], então [tex]n [/tex] é múltiplo de [tex]2[/tex], mas não é múltiplo de [tex]3[/tex].
- Se [tex]n [/tex] deixa resto [tex]3[/tex], então [tex]n [/tex] é múltiplo de [tex]3[/tex], mas não é múltiplo de [tex]2[/tex].
- Se [tex]n [/tex] deixa resto [tex]4[/tex], então [tex]n [/tex] é múltiplo de [tex]2[/tex], mas não é múltiplo de [tex]3[/tex].
- Se [tex]n [/tex] deixa resto [tex]5[/tex], então [tex]n [/tex] não é múltiplo de [tex]2[/tex] e nem [tex]3[/tex].

Se você já consegue entender um pouco o formalismo da Matemática, veja que podemos escrever as informações acima da seguinte maneira:
Um número natural [tex]n [/tex] ao ser dividido por seis deixa resto [tex]0, \, 1, \, 2, \, 3, \, 4 [/tex] ou [tex]5[/tex]. Assim, [tex]n [/tex] pode assumir uma dessas formas:
[tex]\qquad \boxed{6k} \quad \boxed{6k+1} \quad \boxed{6k+2} \quad \boxed{6k+3} \quad \boxed{6k+4} \quad \boxed{6k+5}[/tex], com [tex]k \in \mathbb{N}.[/tex]
- Se [tex]n [/tex] deixa resto [tex]0[/tex], então [tex]n=6k=2(3k)=3(2k) [/tex]. Logo, é múltiplo de [tex]2[/tex] e de [tex]3[/tex] simultaneamente, já que tanto [tex]3k[/tex] como [tex]2k[/tex] são números naturais.
- Se [tex]n [/tex] deixa resto [tex]1[/tex], então [tex]n=6k+1[/tex]. Perceba que [tex]n [/tex] não pode ser escrito na forma [tex]n=2t [/tex] e nem na forma [tex]n=3t [/tex], com [tex]t [/tex] sendo um número natural; assim, [tex]n[/tex] não é múltiplo de [tex]2[/tex] e nem [tex]3[/tex].
- Se [tex]n [/tex] deixa resto [tex]2[/tex], então [tex]n=6k+2=2(3k+1) [/tex] e, portanto, é múltiplo de [tex]2[/tex]. Mas note que não podemos escrever [tex]n[/tex] na forma [tex]n=3t [/tex] com [tex]t [/tex] sendo um número natural; assim, embora seja múltiplo de [tex]2[/tex], [tex]n[/tex] não é múltiplo de [tex]3[/tex].
- Se [tex]n [/tex] deixa resto [tex]3[/tex], então [tex]n=6k+3=3(2k+1) [/tex] e, assim, é múltiplo de [tex]3[/tex]. Mas veja que não é possível escrever [tex]n[/tex] na forma [tex]n=2t [/tex] com [tex]t [/tex] sendo um número natural. Portanto [tex]n[/tex] não é múltiplo de [tex]2[/tex], embora seja múltiplo de [tex]3[/tex].
- Se [tex]n [/tex] deixa resto [tex]4[/tex], então [tex]n=6k+4=2(3k+2) [/tex] e, dessa forma, [tex]n[/tex] é múltiplo de [tex]2[/tex]. Mas também não podemos escrever [tex]n[/tex] na forma [tex]n=3t [/tex] com [tex]t [/tex] sendo um número natural, o que mostra que, embora seja múltiplo de [tex]2[/tex], [tex]n[/tex] não é múltiplo de [tex]3[/tex].
- Se [tex]n [/tex] deixa resto [tex]5[/tex], então [tex]n=6k+5[/tex]. Veja que [tex]n [/tex] não pode ser escrito na forma [tex]n=2t [/tex] e nem na forma [tex]n=3t [/tex], com [tex]t [/tex] sendo um número natural; assim, [tex]n[/tex] não é múltiplo de [tex]2[/tex] e nem [tex]3[/tex].
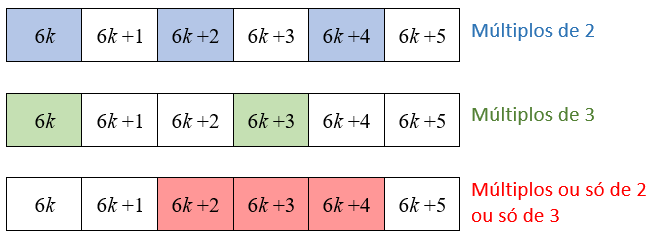
De uma maneira ou de outra, a informação que nos ajudará a resolver o problema é esta:
- Na sequência aparecem números que, quando divididos por seis, deixam resto [tex]2, \, 3[/tex] ou [tex]4.[/tex] Isso significa que foram escritos números da forma [tex]6k+2[/tex], [tex]6k+3[/tex] ou [tex]6k+4[/tex], com [tex]k[/tex] um número natural. Percebam que:
- para [tex]k=0[/tex], aparecem os números [tex]2, \, 3, \, 4[/tex];
- para [tex]k=1[/tex], aparecem os números [tex]8, \, 9, \, 10[/tex];
- para [tex]k=2[/tex], aparecem os números [tex]14, \, 15, \, 16[/tex];
- e assim sucessivamente.
Dessa forma, foram escritos consecutivamente, de [tex]3[/tex] em [tex]3[/tex], números naturais da forma [tex]6k+2[/tex], [tex]6k+3[/tex] ou [tex]6k+4.[/tex] Assim, devemos agrupar as [tex] 2018[/tex] posições de três em três para determinarmos se o número que ocupará a posição [tex] 2018[/tex] será o primeiro, o segundo ou o terceiro no seu respectivo grupo. Observe que
|
[tex]\qquad \qquad \begin{array}{r} 2018 \, \end{array} \begin{array}{|r} \, \, 3 \, \, \, \, \, \\ \hline \end{array}[/tex] [tex]\qquad \qquad\begin{array}{r} \, \, \, \, \, \, 2 \end{array}\begin{array}{r} \, \, \, \, \, 672 \end{array}\qquad \qquad[/tex] |
portanto, devemos formar [tex]672[/tex] grupos de três números e o número que ocupará a posição [tex]2018[/tex] será o segundo número do grupo seguinte.
Fazendo [tex]k=0, \, 1, \, 2, \, \cdots \, , 671[/tex] conseguimos definir os [tex]672[/tex] grupos cujas três posições são ocupadas, respectivamente, pelos números [tex]6k+2[/tex], [tex]6k+3[/tex] e [tex]6k+4[/tex]. Como os números do grupo seguinte serão definidos por [tex]k=672[/tex], o número que ocupará a posição [tex]2018[/tex] será da forma [tex]6k+3[/tex], para [tex]k=672[/tex]. Esse número será [tex] \, \fcolorbox{black}{#eee0e5}{$6\times 672+3=4035$} \, .[/tex]
O esquema abaixo poderá ajudar na visualização da distribuição dos números.
| Grupo 1 | [tex]2[/tex] | [tex]3[/tex] | [tex]4[/tex] | [tex]\boxed{k=0}[/tex] | |||
| Posição 1 | Posição 2 | Posição 3 | |||||
| Grupo 2 | [tex]8[/tex] | [tex]9[/tex] | [tex]10[/tex] | [tex]\boxed{k=1}[/tex] | |||
| Posição 4 | Posição 5 | Posição 6 | |||||
| Grupo 3 | [tex]14[/tex] | [tex]15[/tex] | [tex]16[/tex] | [tex]\boxed{k=2}[/tex] | |||
| Posição 7 | Posição 8 | Posição 9 | |||||
| [tex]\vdots[/tex] | |||||||
| Grupo k+1 | [tex]6k+2[/tex] | [tex]6k+3[/tex] | [tex]6k+4[/tex] | [tex]\boxed{k}[/tex] | |||
| Posição [tex]3k+1[/tex] | Posição [tex]3k+2[/tex] | Posição [tex]3k+3[/tex] | |||||
| [tex]\vdots[/tex] | |||||||
| Grupo 672 | [tex]4028[/tex] | [tex]4029[/tex] | [tex]4030[/tex] | [tex]\boxed{k=671}[/tex] | |||
| Posição 2014 | Posição 2015 | Posição 2016 | |||||
| Grupo 673 | [tex]4034[/tex] | [tex] \, \fcolorbox{black}{#eee0e5}{$4035$}[/tex] | [tex]4036[/tex] | [tex]\boxed{k=672}[/tex] | |||
| Posição 2017 | Posição 2018 | Posição 2019 |
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
