✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Muito Difícil)
(XXVII OPM – 2009) Nos lados [tex]CD [/tex] e [tex]BC [/tex] de um quadrado [tex]ABCD[/tex] são marcados os pontos [tex] N \, [/tex] e [tex] \, M[/tex], respectivamente.
Sabendo que o perímetro do triângulo [tex]MCN[/tex] é igual ao dobro do comprimento do lado do quadrado, determine a medida do ângulo [tex] M\hat AN.[/tex]

AJUDA para a Solução 1

Definição: Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a, \, b, \, h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
Chamamos de tangente de [tex]\theta[/tex], e denotamos por [tex]tg \, \theta[/tex], a razão entre os comprimentos do cateto oposto e do cateto adjacente a [tex]\theta[/tex]:[tex]\boxed{ tg \, \theta= \dfrac{a}{b}}.[/tex]
Propriedade: Dados dois ângulos [tex]a[/tex] e [tex]b[/tex], com [tex]a,b, a+b\neq \dfrac{\pi}{2}+k\pi[/tex], [tex]k\in \mathbb{Z}[/tex], tem-se [tex] \, \boxed{\tan(a+b)=\dfrac{\tan a+\tan b}{1-\tan a\cdot \tan b}} \, .[/tex]
Solução 1
Sejam [tex]l[/tex] o comprimento do lado do quadrado, [tex]n[/tex] o comprimento do segmento [tex]CM[/tex] e [tex]m[/tex] o comprimento do segmento [tex]CN[/tex], conforme indicado na figura abaixo. Na figura, consideramos também que [tex]\textcolor{red}{\theta}[/tex] é a medida em graus do ângulo [tex] M\hat AN.[/tex]
Sabemos que o perímetro do triângulo [tex]MCN[/tex] é igual ao dobro do comprimento do lado do quadrado. Assim, se [tex]x[/tex] for o comprimento do segmento [tex]MN[/tex], segue que:
[tex]\qquad x+m+n=2l[/tex]
[tex]\qquad \boxed{x=2l-m-n}[/tex].
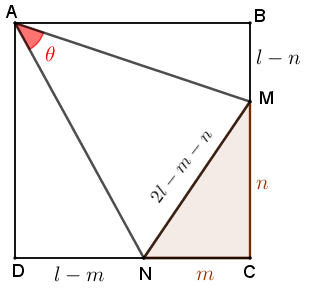
Aplicando o Teorema de Pitágoras no triângulo retângulo [tex]MCN[/tex], temos que:
[tex]\qquad m^2+n^2=\left(2l-m-n \right)^2[/tex]
[tex]\qquad m^2+n^2=4l^2-4lm-4ln+2mn+m^2+n^2[/tex]
[tex]\qquad \cancel{m^2}+\bcancel{n^2}=4l^2-4lm-4ln+2mn+\cancel{m^2}+\bcancel{n^2}[/tex]
[tex]\qquad 0=4l^2-4lm-4ln+2mn[/tex]
[tex]\qquad 2l^2-2lm-2ln+mn=0. \qquad \textcolor{#800000}{(i)}[/tex]
Vamos agora observar os triângulos [tex]ADN[/tex] e [tex]ABM[/tex] para obter a tangente dos ângulos agudos [tex]D\hat{A}N[/tex] e [tex]M\hat{A}B[/tex], cujas medidas em graus denotaremos por [tex]\textcolor{#CC66FF}{\beta}[/tex] e [tex]\textcolor{#00CC00}{\alpha}[/tex], conforme indica a figura a seguir.
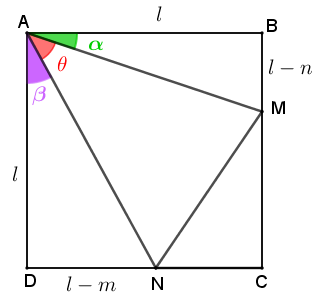
Perceba, então, que:
[tex]\qquad \qquad \textcolor{#00CC00}{tg \, \alpha=\dfrac{l-n}{l}} \qquad \qquad[/tex] e [tex]\qquad \qquad \textcolor{#CC66FF}{tg \, \beta=\dfrac{l-m}{l}}[/tex];
logo, da fórmula da tangente da soma, segue que:
[tex]\qquad tg \, \left(\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta} \right)=\dfrac{ \textcolor{#00CC00}{tg \, \alpha}+\textcolor{#CC66FF}{tg \, \beta}}{1- \textcolor{#00CC00}{tg \, \alpha}\cdot \textcolor{#CC66FF}{tg \, \beta}}[/tex]
[tex]\qquad tg \, \left(\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta} \right)=\dfrac{ \textcolor{#00CC00}{\dfrac{l-n}{l}}+\textcolor{#CC66FF}{\dfrac{l-m}{l}}}{1- \textcolor{#00CC00}{\dfrac{l-n}{l}}\cdot \textcolor{#CC66FF}{\dfrac{l-m}{l}}}=\dfrac{\dfrac{2l-m-n}{l}}{\dfrac{l^2-(l-m)\cdot(l-n)}{l^2}}[/tex]
[tex]\qquad tg \, \left(\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta} \right)=\dfrac{(2l-m-n)\cdot l}{l^2-(l-m)\cdot (l-n)}=\dfrac{2l^2-lm-ln}{l^2-(l^2-ln-lm+mn)}[/tex]
[tex]\qquad tg \, \left(\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta} \right)=\dfrac{2l^2-lm-ln}{ln+lm-mn}[/tex].
De [tex]\textcolor{#800000}{(i)}[/tex], temos que [tex] 2l^2=2lm+2ln-mn[/tex], logo:
[tex]\qquad tg \, \left(\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta} \right)=\dfrac{(2lm+2ln-mn)-lm-ln}{ln+lm-mn}=\dfrac{ln+lm-mn}{ln+lm-mn}[/tex].
[tex]\qquad tg \, \left(\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta} \right)=1[/tex].
Como o ângulo cuja medida é [tex]\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta}[/tex] é um ângulo agudo, segue que [tex]\boxed{\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta}=45^\circ} \, . [/tex]
Mas [tex]\textcolor{#CC66FF}{\beta}+\textcolor{red}{\theta}+\textcolor{#00CC00}{\alpha}=90^\circ[/tex], logo:
[tex]\qquad (\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta})+\textcolor{red}{\theta}=90^\circ[/tex]
[tex]\qquad 45^\circ+\textcolor{red}{\theta}=90^\circ[/tex]
[tex]\qquad \textcolor{red}{\theta}=45^\circ .[/tex]
Portanto, a medida do ângulo [tex] M\hat AN[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$45^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se você ainda não aprendeu trigonometria, não faz mal.
|

Lembretes para a Solução 2
(1) Caso de congruência L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes (geometricamente iguais).
(2) Caso de congruência L.L.L. (lado – lado- lado): Se dois triângulos têm ordenadamente congruentes os três lados, então estes triângulos são congruentes.
✐ Se você não se lembra dos casos de congruência entre triângulos, clique AQUI.
Solução 2
Sejam [tex]l[/tex] o comprimento do lado do quadrado, [tex]n[/tex] o comprimento do segmento [tex]CM[/tex] e [tex]m[/tex] o comprimento do segmento [tex]CN[/tex], conforme indicado na figura abaixo. Na figura, consideramos também que [tex]\textcolor{red}{\theta}[/tex] é a medida em graus do ângulo [tex] M\hat AN.[/tex]
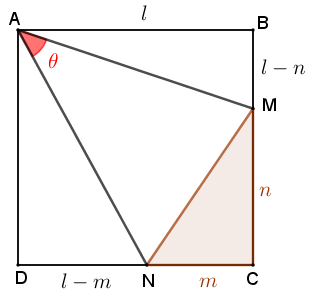
Faremos agora uma construção: seja [tex]E[/tex] o ponto da reta [tex]CD[/tex] tal que [tex]D[/tex] esteja entre os pontos [tex]C[/tex] e [tex]E[/tex] e que o comprimento do segmento [tex]ED[/tex] seja [tex]l-n.[/tex]
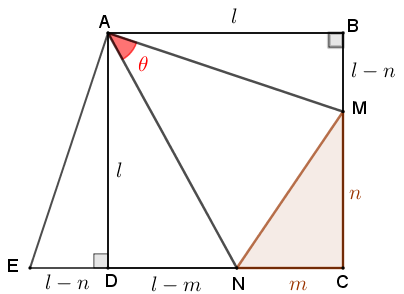
Observe que, pelo Lembrete 1, os triângulos [tex]ADE[/tex] e [tex]ABM[/tex] são congruentes; logo, em particular, os segmentos [tex]\textcolor{#0099FF}{AE}[/tex] e [tex]\textcolor{#0099FF}{AM}[/tex] têm a mesma medida.
Por outro lado, sabemos que o perímetro do triângulo [tex]MCN[/tex] é igual ao dobro do comprimento do lado do quadrado. Assim, se [tex]x[/tex] for o comprimento do segmento [tex]MN[/tex], segue que:
[tex]\qquad x+m+n=2l[/tex]
[tex]\qquad \boxed{x=2l-m-n}[/tex].
Na figura a seguir, vamos passar a limpo algumas informações que nos interessam para a conclusão da solução.
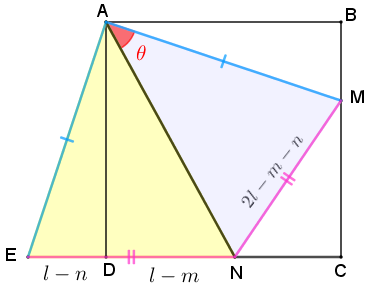
Note que os segmentos [tex]\textcolor{#FF33CC}{EN}[/tex] e [tex]\textcolor{#FF33CC}{NM}[/tex] têm o mesmo comprimento; assim, pelo Lembrete 2, os triângulos [tex]AEN[/tex] e [tex]AMN[/tex] são congruentes.
Vamos fazer uma última figura mostrando algumas igualdades entre medidas de ângulos que podemos obter a partir de congruências dos triângulos que aparecem na figura:
- da congruência dos triângulos [tex]ADE[/tex] e [tex]ABM[/tex], concluímos que os ângulos [tex]\textcolor{#00CC00}{E\hat{A}D}[/tex] e [tex]\textcolor{#00CC00}{M\hat{A}B}[/tex] têm a mesma medida, denotada por [tex]\textcolor{#00CC00}{\alpha}[/tex];
- da congruência dos triângulos [tex]AEN[/tex] e [tex]ANM[/tex], concluímos que os ângulos [tex]\textcolor{red}{E\hat{A}N}[/tex] e [tex]\textcolor{red}{N\hat{A}M}[/tex] têm a mesma medida, denotada por [tex]\textcolor{red}{\theta}[/tex].
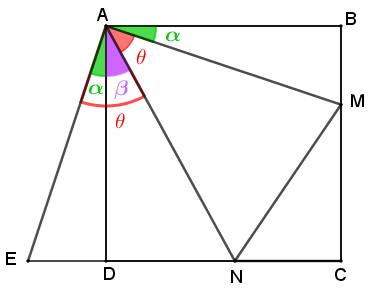
Finalmente, veja que:
[tex]\qquad 90^\circ=\textcolor{#CC66FF}{\beta}+\textcolor{red}{\theta}+\textcolor{#00CC00}{\alpha}[/tex]
[tex]\qquad 90^\circ=(\textcolor{#00CC00}{\alpha}+\textcolor{#CC66FF}{\beta})+\textcolor{red}{\theta}[/tex]
[tex]\qquad 90^\circ=\textcolor{red}{\theta}+\textcolor{red}{\theta}[/tex]
[tex]\qquad 90^\circ=2\textcolor{red}{\theta}[/tex]
[tex]\qquad \textcolor{red}{\theta}=\dfrac{90^\circ}{2}[/tex]
[tex]\qquad \textcolor{red}{\theta}=45^\circ.[/tex]
Portanto, a medida do ângulo [tex] M\hat AN[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$45^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
