✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 9ª série do E. F.- Nível de dificuldade: Médio)
A partir das informações que aparecem na figura abaixo, determine a medida angular [tex]\theta[/tex], sabendo que as retas [tex]r[/tex] e [tex]s[/tex] são paralelas.
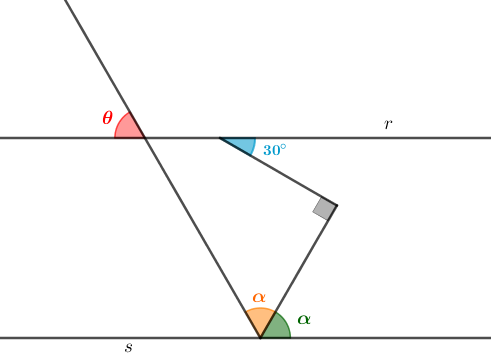
Adaptado de Matemática1.com.

Lembretes
(1) Se duas retas paralelas são intersectadas por uma transversal, então os pares de ângulos alternos internos que essa transversal define são congruentes.
(2) Se duas retas paralelas são intersectadas por uma transversal, então os pares de ângulos correspondentes que essa transversal define são congruentes.
(Precisa relembrar esses conceitos? Dê uma passadinha nesta Sala.)
(3) A soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ\,.[/tex]
Solução
Observe que o prolongamento do segmento que define o ângulo de [tex]\textcolor{#0099CC}{30^\circ}[/tex] na figura original é uma transversal das retas paralelas [tex]r[/tex] e [tex]s[/tex]. Então, podemos considerar o par de ângulos alternos internos que essa transversal define, conforme indicado na figura a seguir. O Lembrete (1) garante que o segundo ângulo do par tem [tex]\textcolor{#0099CC}{30^\circ}[/tex] como medida.
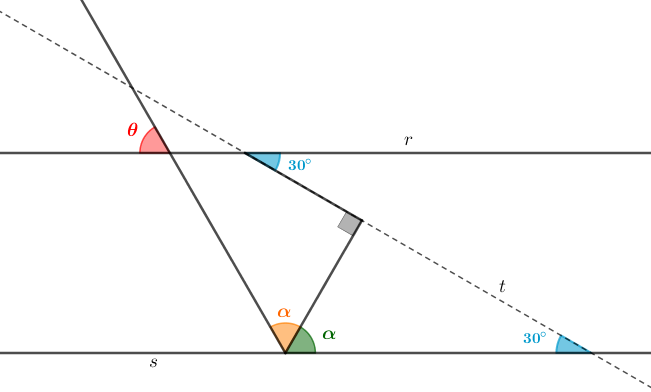
Dessa forma, fica determinado o triângulo retângulo [tex]ABC[/tex] indicado na próxima figura.
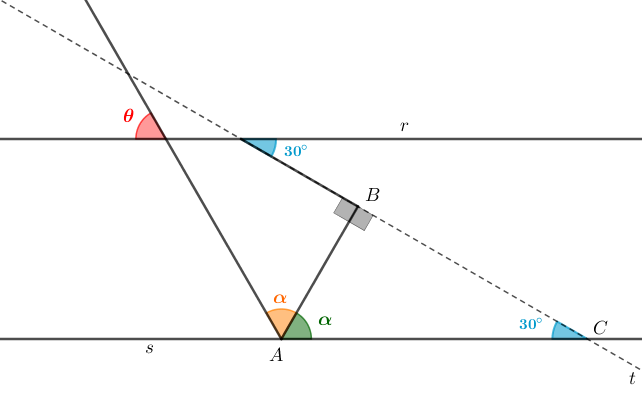
Assim, pelo Lembrete (3), segue que:
[tex]\qquad \alpha+90^\circ+30^\circ=180^\circ\\
\qquad \alpha+120^\circ=180^\circ\\
\qquad \alpha=180^\circ-120^\circ\\
\qquad \boxed{\alpha=60^\circ}\,.[/tex]
Mas a transversal às retas paralelas [tex]r[/tex] e [tex]s[/tex] que define o ângulo de medida [tex]\textcolor{#FF0000}{\theta}[/tex] também define um par de ângulos correspondentes, como mostra a figura a seguir. O Lembrete (2) garante que esses dois ângulos têm a mesma medida.
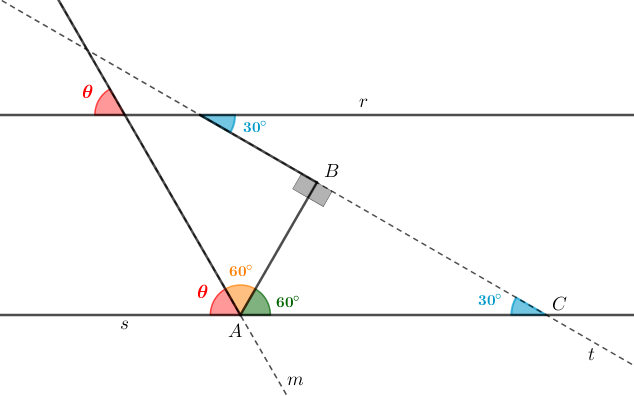
Finalmente, observando os três ângulos com vértices no ponto [tex]A[/tex], concluímos que:
[tex]\qquad \textcolor{#FF0000}{\theta}+\textcolor{#FF6600}{60^\circ}+\textcolor{#009900}{60^\circ}=180^\circ[/tex]
e, portanto, [tex]\fcolorbox{black}{#eee0e5}{$\theta=60^\circ$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
