✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Fácil)
Ao recortarmos os três ângulos do triângulo abaixo e reagrupá-los formando a figura da direita, que propriedade geométrica fica ilustrada?
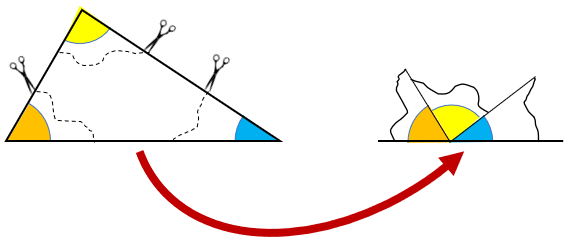

Lembretes
(1) Ângulos correspondentes definidos por duas retas paralelas e uma reta transversal são congruentes. (Se você não se lembra do assunto, não deixe de dar uma passadinha nesta Sala para Leitura.)
(2) A soma dos ângulos internos de um polígono convexo de [tex]n[/tex] lados ([tex]n\gt 2[/tex]) é dada por:
[tex]\qquad \qquad \boxed{S_{i_n}=\left(n-2\right)\cdot 180^\circ}.[/tex]
Solução
O problema propõe que recortemos três regiões internas de um triângulo, de modo que cada região contenha parte dos três ângulos internos desses triângulos. Suponhamos que as medidas em graus desses ângulos sejam [tex]a, \, b, \, c.[/tex]
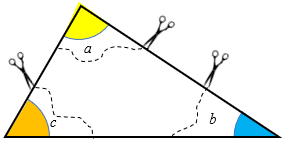
Depois de recortá-las, unimos as três regiões por um vértice comum e sobrepondo dois lados de duas delas e, em seguida, sobrepondo dois lados da segunda e da terceira regiões, conforme mostra a segunda imagem do problema. Observe que as medidas dos três ângulos assinalados não se modificaram, pois as três regiões mantiveram suas respectivas formas. Observe também que os três ângulos em questão formaram o que chamamos de um ângulo raso, ou seja, um ângulo cuja medida em graus é [tex]180[/tex].
Como esse ângulo de [tex]180^\circ[/tex] é a soma dos ângulos coloridos, concluímos que [tex]\boxed{a+b+c=180^\circ}.[/tex]
Dessa forma, temos uma ilustração de uma importante propriedade da Geometria:
- A soma em graus das medidas dos três ângulos internos de um triângulo é [tex]180^\circ.[/tex]
Um applet para ajudar
O applet abaixo simula o processo de construção da figura final do problema, a partir de três triângulos internos que foram recortados do triângulo inicial.
Movimente esses três triângulos internos recortados de modo que seus ângulos coloridos definam um ângulo de [tex]180^\circ.[/tex] Você pode utilizar a linha abaixo do triângulo para construir o ângulo.
Instruções:
(1) Espere o aplicativo carregar completamente.
(2) Para fazer a translação de um triângulo recortado, clique no respectivo ponto vermelho, mantenha o mouse pressionado e faça o movimento.
(3) Para fazer a rotação de um triângulo recortado, clique no respectivo ponto azul, mantenha o mouse pressionado e faça o movimento.
(4) Para retornar à posição inicial, clique no centro das setinhas circulares que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
