.Problema para ajudar na escola: Uma gincana de fim de semana

Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Muito Difícil)

O colégio Reino Feliz vai promover uma grande gincana para seus alunos com mais de onze anos no próximo final de semana e definiu o seguinte critério para a formação das equipes participantes:

• Cada equipe deve ter mais de [tex]20[/tex] e menos de [tex]25[/tex] alunos.
• Em cada equipe, o número de alunos com menos de catorze anos deve ser menor do que [tex]10[/tex] e maior que a metade do número de alunos com catorze anos ou mais.

De quantas maneiras distintas os alunos poderão montar as suas equipes?

Solução

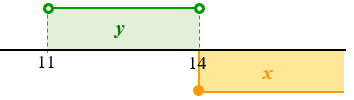
Dessa forma, as informações matemáticas que podemos extrair do enunciado do problema são as seguintes:

► Cada equipe deve ter mais de [tex]20[/tex] e menos de [tex]25[/tex] alunos:
[tex]\qquad \begin{cases}x+y \gt 20\\ x+y \lt 25 \end{cases}[/tex].
► O número de alunos com menos de catorze anos deve ser menor do que [tex]10[/tex]:
[tex]\qquad y \lt 10.[/tex]
► O número de alunos com menos de catorze anos deve ser maior que a metade do número de alunos com catorze anos ou mais:
[tex]\qquad y \gt \dfrac{x}{2}.[/tex]

Assim, o sistema de desigualdades que descreve todas as possíveis formações das equipes participantes da gincana é o seguinte:

[tex]\begin{cases}x\geqslant 0 \\ y\geqslant 0 \\y \gt 20-x\\ y \lt 25 -x\\y \lt 10\\y \gt \dfrac{x}{2} \end{cases}\quad[/tex],

lembrando que estamos interessados em soluções naturais.
Um sistema formado por desigualdades e com muitas soluções pode ser solucionado graficamente. Vejamos, portanto, como fica a solução desse sistema de desigualdades em um plano cartesiano [tex]xOy.[/tex]

• As soluções desse sistema são os pontos [tex]P=(x,y)[/tex] do plano cartesiano tais que [tex] x\geqslant 0 [/tex] e [tex] y\geqslant 0 [/tex] e que satisfazem simultaneamente às seguintes condições:

[tex] \boxed{y \gt 20-x}; \quad \quad \boxed{y \lt 25 -x}; \quad \quad \boxed{y \lt 10} \quad\quad \text{e} \quad\quad\boxed{y \gt \dfrac{x}{2}}\,.[/tex]

Vamos estudar cada uma dessas condições isoladamente em [tex]\mathbb{R} \times \mathbb{R}[/tex], com [tex]x\geqslant 0[/tex] e [tex]y\geqslant 0[/tex], para depois analisarmos as quatro simultaneamente e, por fim, escolhermos os pontos com coordenadas naturais.

• [tex]y \gt 20-x[/tex]

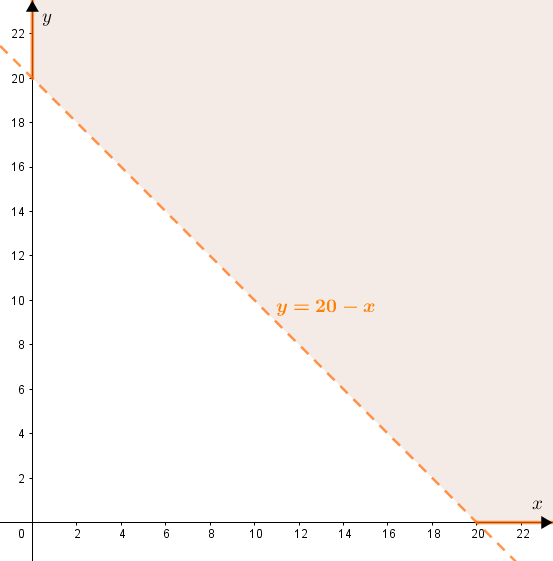
Os pontos [tex]P=(x,y)[/tex] com [tex]x\geqslant 0[/tex] e [tex]y\geqslant 0[/tex] que satisfazem esta condição são aqueles que estão:
– acima da reta [tex]y = 20-x[/tex];
– à direita ou sobre o eixo [tex]Oy[/tex];
– acima ou sobre o eixo [tex]Ox[/tex].



• [tex]y \lt 25-x[/tex]

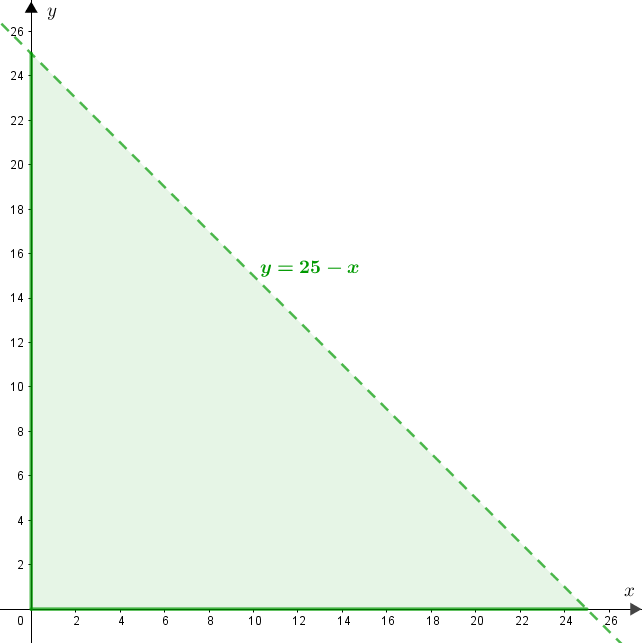
Os pontos [tex]P=(x,y)[/tex] com [tex]x\geqslant 0[/tex] e [tex]y\geqslant 0[/tex] que satisfazem esta condição são aqueles que estão:
– abaixo da reta [tex]y=25-x[/tex];
– à direita ou sobre o eixo [tex]Oy[/tex];
– acima ou sobre o eixo [tex]Ox[/tex].



• [tex]y \lt 10[/tex]

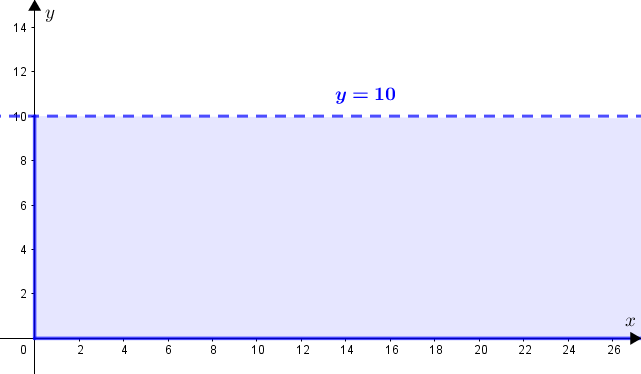
Os pontos [tex]P=(x,y)[/tex] com [tex]x\geqslant 0[/tex] e [tex]y\geqslant 0[/tex] que satisfazem esta condição são aqueles que estão:
– abaixo da reta [tex]y=10[/tex];
– à direita ou sobre o eixo [tex]Oy[/tex];
– acima ou sobre o eixo [tex]Ox[/tex].



• [tex]y \gt \dfrac{x}{2}[/tex]

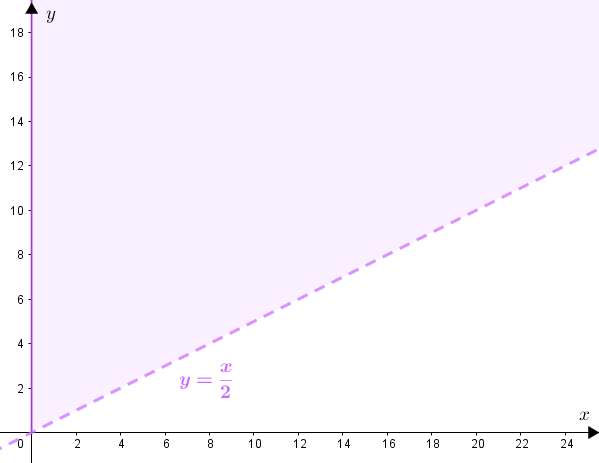
Os pontos [tex]P=(x,y)[/tex] com [tex]x\geqslant 0[/tex] e [tex]y\geqslant 0[/tex] que satisfazem esta condição são aqueles que estão:
– acima da reta [tex]y=\dfrac{x}{2}[/tex];
– à direita ou sobre o eixo [tex]Oy[/tex];
– acima ou sobre o eixo [tex]Ox[/tex].



Fazendo a interseção das quatro regiões acima, obtemos a solução em [tex]\mathbb{R} \times \mathbb{R}[/tex] do sistema em questão.



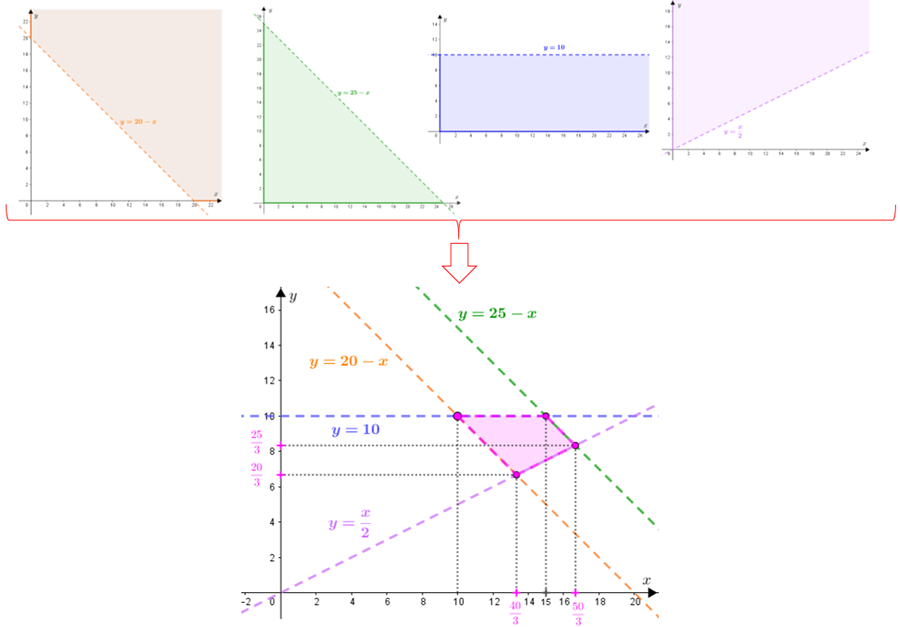
Os quatro pontos que definem a região foram obtidos fazendo a interseção das respectivas retas que os definem:

► retas [tex]y=10[/tex] e [tex]y=20-x[/tex] Substituindo [tex]y=10[/tex] em [tex]y=20-x[/tex], segue que: [tex]\qquad y=20-x[/tex] [tex]\qquad 10=20-x[/tex] [tex]\qquad x=10[/tex]. Assim, o ponto de interseção tem coordenadas [tex](10,10).[/tex]

► retas [tex]y=10[/tex] e [tex]y=25-x[/tex] Substituindo [tex]y=10[/tex] em [tex]y=25-x[/tex], segue que: [tex]\qquad y=25-x[/tex] [tex]\qquad 10=25-x[/tex] [tex]\qquad x=15[/tex]. Assim, o ponto de interseção tem coordenadas [tex](15,10)[/tex].

► retas [tex]y=\dfrac{x}{2}[/tex] e [tex]y=25-x[/tex] Substituindo [tex]y=\dfrac{x}{2}[/tex] em [tex]y=25-x[/tex], segue que: [tex]\qquad y=25-x\\ \qquad \dfrac{x}{2}=25-x\\ \qquad \dfrac{3x}{2}=25[/tex] [tex]\qquad x=\dfrac{50}{3}[/tex]. Agora, substituindo [tex] x=\dfrac{50}{3}[/tex] em [tex]y=25-x[/tex], segue que: [tex]\qquad y=25-x\\ \qquad y=25-\dfrac{50}{3}\\ \qquad y=\dfrac{25}{3}[/tex] Assim, o ponto de interseção tem coordenadas [tex]\left(\dfrac{50}{3},\dfrac{25}{3}\right).[/tex]

► retas [tex]y=\dfrac{x}{2}[/tex] e [tex]y=20-x[/tex] Substituindo [tex]y=\dfrac{x}{2}[/tex] em [tex]y=20-x[/tex], segue que: [tex]\qquad y=20-x\\ \qquad \dfrac{x}{2}=20-x\\ \qquad \dfrac{3x}{2}=20[/tex] [tex]\qquad x=\dfrac{40}{3}[/tex]. Agora, substituindo [tex] x=\dfrac{40}{3}[/tex] em [tex]y=20-x[/tex], segue que: [tex]\qquad y=20-x\\ \qquad y=20-\dfrac{40}{3}\\ \qquad y=\dfrac{20}{3}[/tex] Assim, o ponto de interseção tem coordenadas [tex]\left(\dfrac{40}{3},\dfrac{20}{3}\right).[/tex]

Assim, a solução geométrica do sistema em questão em [tex]\mathbb{R} \times \mathbb{R}[/tex], com [tex]x\geqslant 0[/tex] e [tex]y\geqslant 0[/tex], é a seguinte:

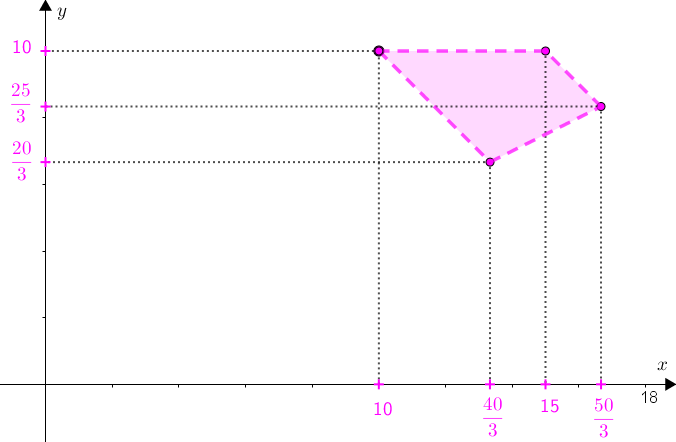
A última etapa da nossa solução é determinar os pontos [tex]P=(x,y)[/tex] da região cujas coordenadas são números naturais. Observe, então, a figura a seguir.

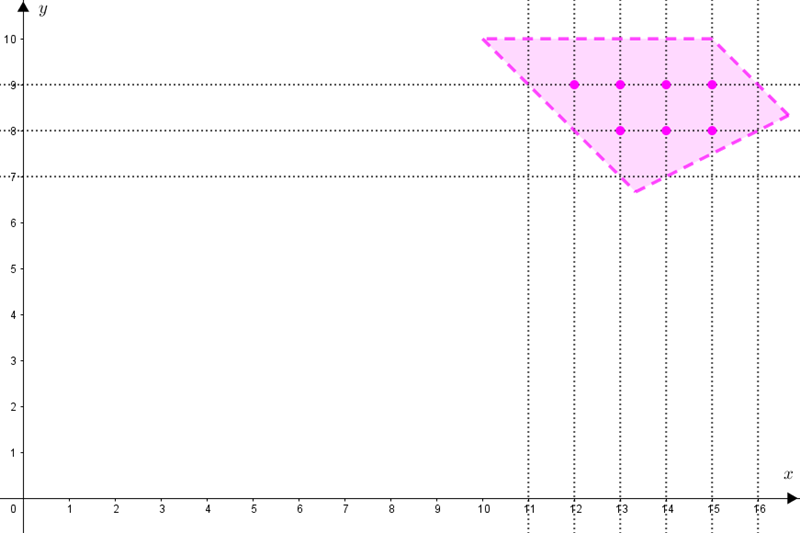
As soluções do sistema com coordenadas naturais são os pontos:

• [tex](12,9)\,;\, (13,8) \,;\, (13,9)\,;\, (14,8)\,;\, (14,9)\,;\, (15,8)\,;\, (15,9)[/tex];

assim, as possíveis maneiras com que os alunos poderão montar as suas equipes são as seguintes:

[tex]\begin{array}{|c|c| c| c |c |c|}
\hline
\text{alunos com “catorze anos ou mais”}&12&13&13&14&14&15&15\\
\hline
\text{alunos com “menos que catorze anos”}&9&8&9&8&9&8&9\\
\hline
\end{array}[/tex]

Portanto, existem [tex] \fcolorbox{black}{#ffd3d3}{$\text{sete}$}[/tex] maneiras distintas de os alunos montarem as suas equipes.

Solução elaborada pelos Moderadores do Blog.