✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
Qual a medida do raio da circunferência inscrita em um triângulo retângulo isósceles cujos lados congruentes medem [tex]6 \, cm[/tex] cada?

Lembretes
Informações importantes sobre triângulos e circunferências:
✐ O centro da circunferência inscrita em um triângulo é o incentro, que é o encontro das três bissetrizes internas desse triângulo.(Bissetriz de um triângulo é um segmento com extremidades em um vértice e no respectivo lado oposto e que divide o ângulo interno definido por esse vértice em dois ângulos com a mesma medida.)
✐ A bissetriz relativa à base de um triângulo isósceles também é uma mediana e uma altura.
✐ Toda tangente a uma circunferência é perpendicular ao raio no ponto de tangência.
Notação
Denotaremos o segmento definido por dois pontos genéricos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].
Solução 1
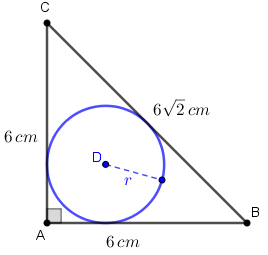
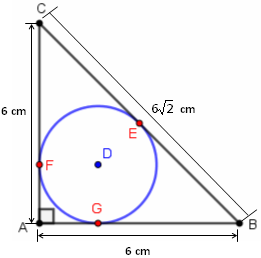 A figura ao lado mostra os dados do nosso problema, a partir de um triângulo retângulo isósceles [tex]ABC[/tex]. Como a hipotenusa de um triângulo retângulo é o maior dos seus três lados, se esse triângulo retângulo é isósceles, isso significa que os lados congruentes são os seus catetos. Assim, o terceiro lado do triângulo [tex]ABC[/tex] é sua hipotenusa e, no nosso caso, se o comprimento dessa hipotenusa for [tex]h[/tex], então, pelo Teorema de Pitágoras:
A figura ao lado mostra os dados do nosso problema, a partir de um triângulo retângulo isósceles [tex]ABC[/tex]. Como a hipotenusa de um triângulo retângulo é o maior dos seus três lados, se esse triângulo retângulo é isósceles, isso significa que os lados congruentes são os seus catetos. Assim, o terceiro lado do triângulo [tex]ABC[/tex] é sua hipotenusa e, no nosso caso, se o comprimento dessa hipotenusa for [tex]h[/tex], então, pelo Teorema de Pitágoras:[tex]\qquad h^2=6^2+6^2[/tex]
[tex]\qquad h=\sqrt{2\cdot 6^2}[/tex]
[tex]\qquad h=6\sqrt{2} \, cm.[/tex]
Uma circunferência inscrita em um triângulo tangencia esse triângulo em três pontos. No nosso caso, esses pontos foram denotados por [tex]E[/tex] , [tex]F[/tex] e [tex]G.[/tex] O ponto [tex]D[/tex] mostrado na figura é o centro da circunferência inscrita no triângulo [tex]ABC.[/tex]
 Mas o que sabemos sobre a circunferência inscrita no triângulo [tex]ABC \, [/tex]?
Mas o que sabemos sobre a circunferência inscrita no triângulo [tex]ABC \, [/tex]?
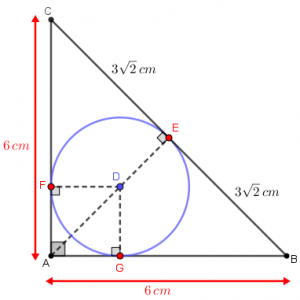
- Utilizando simultaneamente os três lembretes, concluímos que o segmento [tex]\overline{AE}[/tex] é perpendicular ao lado [tex]\overline{BC}[/tex], contém o centro [tex]D \, [/tex] e [tex] \, E[/tex] é o ponto médio de [tex]\overline{BC}[/tex]. Assim as medidas dos segmentos [tex]\overline{BE}[/tex] e [tex]\overline{EC}[/tex] são iguais a [tex]3\sqrt{2} \, cm \, .[/tex]
- Pelo terceiro lembrete:
- os segmentos [tex]\overline{DF}[/tex] e [tex]\overline{AC}[/tex] são perpendiculares.
- os segmentos [tex]\overline{DG}[/tex] e [tex]\overline{AB}[/tex] são perpendiculares.
Registramos essas conclusões na segunda figura lateral.
Aproveitando essa segunda figura, observamos que o Teorema de Pitágoras nos fornece a medida [tex]x[/tex] do segmento [tex]\overline{AE} \, [/tex]:
[tex]\qquad x^2+\left(3\sqrt{2}\right)^2=6^2[/tex]
[tex]\qquad x^2+18=36[/tex]
[tex]\qquad x=\sqrt{18}[/tex]
[tex]\qquad x=\sqrt{2\cdot 9}[/tex]
[tex]\qquad x=3\sqrt{2} \, cm.[/tex]
Estamos aptos a resolver o problema; para isso, observemos a última figura.
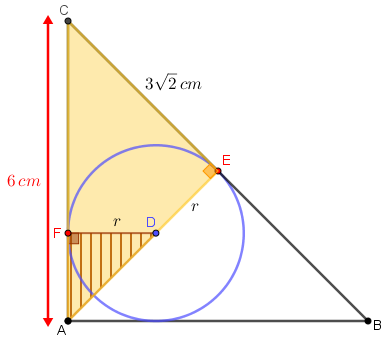 Perceba que os triângulos [tex]FAD[/tex] e [tex]EAC[/tex] são semelhantes, pois ambos têm um ângulo reto e o ângulo de vértice [tex]A[/tex] é comum aos dois.
Perceba que os triângulos [tex]FAD[/tex] e [tex]EAC[/tex] são semelhantes, pois ambos têm um ângulo reto e o ângulo de vértice [tex]A[/tex] é comum aos dois.
Dessa forma
[tex]\qquad \qquad \dfrac{AD}{AC}=\dfrac{FD}{CE} \, [/tex],
donde:
[tex]\qquad \qquad \dfrac{3\sqrt{2}-r}{6}=\dfrac{r}{3\sqrt{2}} \, .[/tex]
Assim, segue que:
[tex]\quad 3\sqrt{2}\cdot\left(3\sqrt{2}-r\right)=6r[/tex]
[tex]\quad \left(3\sqrt{2}\right)^2-3\sqrt{2}\,r=6r[/tex]
[tex]\quad \left(3\sqrt{2}\right)^2=r\left(6+3\sqrt{2}\right)[/tex]
[tex]\quad 18=r\left(6+3\sqrt{2}\right)[/tex]
donde,
[tex]\quad r=\dfrac{18}{6+3\sqrt{2}}=\dfrac{18}{6+3\sqrt{2}} \, \cdot \, \dfrac{6-3\sqrt{2}}{6-3\sqrt{2}}[/tex]
[tex]\quad r=\dfrac{18\cdot \left(6-3\sqrt{2}\right)}{6^2-\left(3\sqrt{2}\right)^2}=\dfrac{18\cdot \left(6-3\sqrt{2}\right)}{36-18}[/tex]
[tex]\quad r=\dfrac{\cancel{18}\cdot \left(6-3\sqrt{2}\right)}{\cancel{18}}=6-3\sqrt{2}.[/tex]
Pelo exposto, a medida do raio da circunferência inscrita no triângulo [tex]ABC[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$6-3\sqrt{2}\,cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
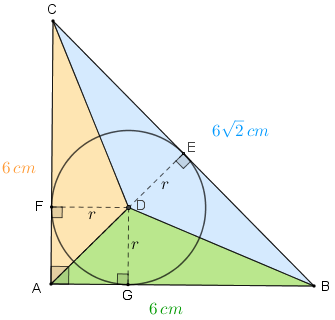 A partir da informação obtida na primeira solução de que a hipotenusa do triângulo retângulo [tex]ABC[/tex] mede [tex]6\sqrt{2} \, cm[/tex], podemos utilizar o terceiro lembrete e obter a figura ao lado.
A partir da informação obtida na primeira solução de que a hipotenusa do triângulo retângulo [tex]ABC[/tex] mede [tex]6\sqrt{2} \, cm[/tex], podemos utilizar o terceiro lembrete e obter a figura ao lado.Para solucionar o problema, basta observar que a área do triângulo [tex]ABC[/tex] é a soma das áreas dos triângulos [tex]ADB \, [/tex], [tex]BDC\,[/tex] e [tex]\,CDA[/tex]. Vamos, então, calcular essas áreas.
- Área do triângulo [tex]ABC[/tex]:
[tex]\qquad S=\dfrac{\text{base}\times \text{altura}}{2}=\dfrac{AB \times CA}{2}[/tex]
[tex]\qquad S=\dfrac{6 \times 6}{2}=\dfrac{36}{2}=18 \, cm^2[/tex] - Área do triângulo [tex]ADB[/tex]:
[tex]\qquad S_1=\dfrac{\text{base}\times \text{altura}}{2}=\dfrac{AB \times DG}{2}[/tex]
[tex]\qquad S_1=\dfrac{6 \times r}{2}=3r \, cm^2[/tex] - Área do triângulo [tex]BDC[/tex]:
[tex]\qquad S_2=\dfrac{\text{base}\times \text{altura}}{2}=\dfrac{BC\times DE}{2}[/tex]
[tex]\qquad S_2=\dfrac{6\sqrt{2} \times r}{2}=3\sqrt{2}r \, cm^2[/tex] - Área do triângulo [tex]CDA[/tex]:
[tex]\qquad S_3=\dfrac{\text{base}\times \text{altura}}{2}=\dfrac{CA\times DF}{2}[/tex]
[tex]\qquad S_3=\dfrac{6 \times r}{2}=3r \, cm^2[/tex]
Como [tex]S=S_1+S_2+S_3 \, [/tex], segue que:
[tex]\qquad 18=3r+3\sqrt{2}r+3r=6r+3\sqrt{2}r=\left(6+3\sqrt{2}\right)\,r[/tex]
e, assim,
[tex]\qquad r=\dfrac{18}{6+3\sqrt{2}}=\dfrac{18}{6+3\sqrt{2}} \, \cdot \, \dfrac{6-3\sqrt{2}}{6-3\sqrt{2}}=\dfrac{18\cdot \left(6-3\sqrt{2}\right)}{6^2-\left(3\sqrt{2}\right)^2}[/tex]
[tex]\qquad r=\dfrac{18\cdot \left(6-3\sqrt{2}\right)}{36-18}=\dfrac{\cancel{18}\cdot \left(6-3\sqrt{2}\right)}{\cancel{18}}=6-3\sqrt{2}.[/tex]
Mais uma vez, obtivemos que a medida do raio da circunferência inscrita no triângulo [tex]ABC[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$6-3\sqrt{2}\,cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se você repetir o raciocínio que fizemos na Solução 2 para um triângulo qualquer, você vai obter uma fórmula muito útil para o cálculo da área de um triângulo: |
Solução 3
 A partir da informação de que a hipotenusa do triângulo retângulo [tex]ABC[/tex] mede [tex]6\sqrt{2} \, cm \, [/tex], vamos utilizar a fórmula [tex]\boxed{ S=p\cdot r}[/tex] para solucionar rapidamente o problema. Observe:
A partir da informação de que a hipotenusa do triângulo retângulo [tex]ABC[/tex] mede [tex]6\sqrt{2} \, cm \, [/tex], vamos utilizar a fórmula [tex]\boxed{ S=p\cdot r}[/tex] para solucionar rapidamente o problema. Observe:
[tex]\quad S=p\cdot r[/tex]
[tex]\quad 18=\dfrac{6+6+6\sqrt{2}}{2}\cdot r=\dfrac{12+6\sqrt{2}}{2}\cdot r=\dfrac{6\cdot (2+\sqrt{2})}{2}\cdot r[/tex]
[tex]\quad 18=\dfrac{\cancel{6}\cdot (2+\sqrt{2})}{\cancel{2}}\cdot r=3\cdot(2+\sqrt{2})\cdot r[/tex]
[tex]\quad \cancel{18}=\cancel{3}\cdot(2+\sqrt{2})\cdot r[/tex]
[tex]\quad 6=2+\sqrt{2}\cdot r[/tex]
[tex]\quad r=\dfrac{6}{2+\sqrt{2}}=\dfrac{6}{2+\sqrt{2}} \, \cdot \, \dfrac{2-\sqrt{2}}{2-\sqrt{2}}=\dfrac{6\cdot(2-\sqrt{2})}{2^2-\left(\sqrt{2}\right)^2}=\dfrac{6\cdot(2-\sqrt{2})}{4-2}[/tex]
[tex]\quad r=\dfrac{6\cdot(2-\sqrt{2})}{2}=\dfrac{\cancel{6}\cdot(2-\sqrt{2})}{\cancel{2}}=3\cdot(2-\sqrt{2})[/tex]
[tex]\quad \, \fcolorbox{black}{#eee0e5}{$r=6-3\sqrt{2}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Use o applet abaixo para visualizar alguns triângulos e, particularmente, verificar a validade da fórmula [tex]\boxed{ S=p\cdot r}[/tex]. |
Um applet para ajudar. . .
Instruções:
1) Aguarde o aplicativo carregar completamente.
2) Para modificar a forma e as medidas do triângulo [tex]ABC[/tex], clique sobre o ponto [tex]C[/tex] e, mantendo o mouse pressionado, movimente-o.
3) Para cada triângulo obtido, você encontrará registrados no applet dados que permitem verificar a área do triângulo [tex]ABC[/tex] de três modos:
- utilizando a fórmula [tex]\boxed{\dfrac{\text{base}\times \text{altura}}{2}} \, [/tex],
- utilizando a fórmula [tex]\boxed{p \times r} \, [/tex],
- utilizando a soma dos triângulos internos definidos pelos vértices [tex]A, \, B, \, C[/tex] e o centro da circunferência inscrita.
4) Lembre-se de que o GeoGebra fornece valores aproximados para as medidas apresentadas.
5) Utilize as setinhas que aparecem no canto superior direita, para voltar à configuração inicial do triângulo [tex]ABC.[/tex]
OBMEP_srg, criado com o GeoGebra
Observamos que o applet ajuda na visualização do resultado;
mas, matematicamente, não substitui sua demonstração.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
