✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
No interior de um quadrado de lados com comprimento [tex]6 \, cm[/tex], foi feito o desenho colorido mostrado na imagem abaixo.
A região colorida foi traçada a partir de arcos de circunferências com centros nos vértices do quadrado, todos passando pelo centro do quadrado.
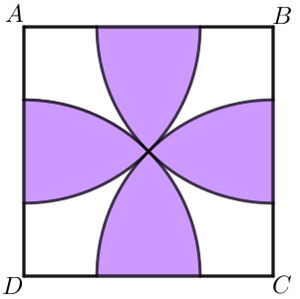
Qual a medida da área colorida?
Solução
Conforme indicado na figura a seguir, denotaremos por:
- [tex]O[/tex] o centro do quadrado [tex]ABCD[/tex];
- [tex]M_1[/tex] o ponto médio do lado [tex]AB[/tex];
- [tex]M_2[/tex] o ponto médio do lado [tex]BC[/tex];
- [tex]M_3[/tex] o ponto médio do lado [tex]CD[/tex];
- [tex]M_4[/tex] o ponto médio do lado [tex]DA[/tex];
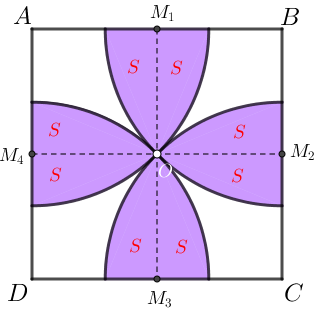
Observe que os segmentos [tex]OM_1[/tex], [tex]OM_2[/tex], [tex]OM_3[/tex], [tex]OM_4[/tex] dividem a região colorida em oito partes iguais, cada uma com medida de área [tex]S.[/tex]
A figura abaixo nos mostra que um quarto da área do círculo de raio [tex] OC[/tex] é igual à área de [tex]2S [/tex] mais a área do quadrado [tex]OM_{3} CM_{2}[/tex]; logo, [tex]2S[/tex] corresponde à diferença entre as medidas das áreas de um quarto do círculo de raio [tex]OC[/tex] e de um quadrado cujos lados medem a metade do comprimento dos lados do quadrado original [tex]ABCD[/tex].
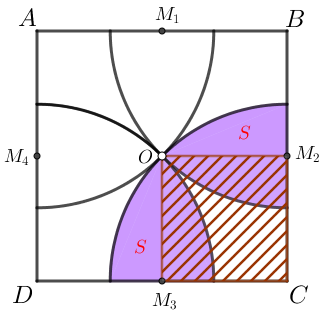
- Como os lados do quadrado [tex]ABCD[/tex] medem [tex]6 \, cm[/tex], os lados do quadrado menor medem [tex]3 \, cm[/tex] e, consequentemente, sua área mede [tex]\boxed{9 \, cm^2}.\qquad \textcolor{#800000}{(i)}[/tex]
- Note que o segmento [tex]OC[/tex] é a diagonal do quadrado [tex]OM_2CM_3[/tex] cujos lados sabemos que medem [tex]3 \, cm[/tex]; assim, se [tex]x[/tex] for a medida em centímetros de [tex]OC[/tex], pelo Teorema de Pitágoras segue que:
[tex]\qquad \qquad x^2=3^2+3^2\\
\qquad \qquad x^2=18\\
\qquad \qquad x=3\sqrt{2} \, cm.[/tex]
Dessa forma, a medida da área de um quarto do círculo de raio [tex]OC[/tex] é dada por [tex] \boxed{\dfrac{\pi\left(3\sqrt{2} \right)^2}{4}=\dfrac{9\pi}{2} \, cm^2}.\qquad \textcolor{#800000}{(ii)}[/tex]
Portanto, por [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], temos que [tex] 2S=\left(\dfrac{9\pi}{2}-9\right) \, cm^2.[/tex]
Finalmente, podemos calcular a medida da área colorida, já que esta é igual a [tex]8S:[/tex]
[tex]\qquad 8S=4\times(2S)=4 \times \left(\dfrac{9\pi}{2}-9\right)= (18\pi-36) \, cm^2.[/tex]
Logo, a medida da área colorida dada no problema é [tex] \, \fcolorbox{black}{#e2cef7}{$18(\pi-2) \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
