.Problema para ajudar na escola: Uma área amarela

✏ Link do problema para dispositivos da Apple.

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)

Os vértices do quadrado [tex]ABCD[/tex] são pontos da circunferência exibida na figura e [tex]\stackrel{\frown}{BD}[/tex] é um arco da circunferência de centro em [tex]A[/tex] e raio [tex]AB[/tex].

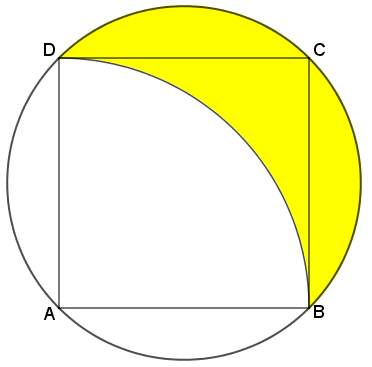
Sabendo que cada lado do quadrado mede [tex]2~cm[/tex], determine a área da região colorida de amarelo.

Solução

Para solucionar este problema, vamos calcular várias áreas. Observe!

  • O triângulo [tex]BAD[/tex] é retângulo; assim, do teorema de Pitágoras, segue que:

    • [tex]\qquad DB\,^2=AD\,^2+AB\,^2[/tex]
    [tex]\qquad DB\,^2=2\,^2+2\,^2[/tex]
    [tex]\qquad DB\,^2=8[/tex]
    [tex]\qquad DB=\sqrt{8}=2\,\sqrt{2}.[/tex]
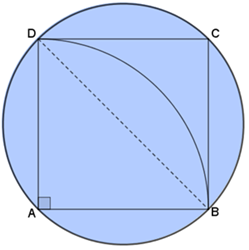
    Como o segmento [tex]\overline{DB}[/tex] é o diâmetro do círculo externo da figura, segue que a área [tex]\textcolor{#6699FF}{A_{circ}}[/tex] desse círculo é:
    [tex]\qquad \textcolor{#6699FF}{A_{circ}=\pi \left(\dfrac{2\,\sqrt{2}}{2}\right)^2=2\,\pi\;cm^2}[/tex].

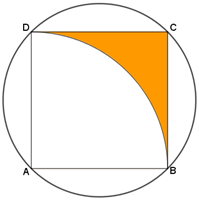
  • A área [tex] \textcolor{#FF9900}{S_1}[/tex] da região limitada pelos segmentos [tex]\overline{DC}[/tex], [tex]\overline{CB}[/tex] e pelo arco [tex]\stackrel{\frown}{BD}[/tex] é igual à área do quadrado [tex]ABCD[/tex] menos um quarto da área do círculo de centro em [tex]A[/tex] e raio [tex]AB[/tex].

    • Assim:
    [tex]\qquad \textcolor{#FF9900}{S_1=2^2-\dfrac{\pi\,\left(2\right)^2}{4}=4-\pi\,\,cm^2}[/tex].

  • A área [tex] \textcolor{#00CC00}{S_2}[/tex] da região limitada pelo segmento [tex]\overline{DC}[/tex] e pelo arco [tex]\stackrel{\frown}{DC}[/tex] é a quarta parte da diferença entre a área [tex]\textcolor{#6699FF}{A_{circ}}[/tex] do círculo externo e a área do quadrado [tex]ABCD\,.[/tex]
    Logo:
    [tex]\qquad \textcolor{#00CC00}{S_2}=\dfrac{\textcolor{#6699FF}{2\,\pi}-4}{4}\textcolor{#00CC00}{=\dfrac{\pi-2}{2}\,cm^2}[/tex].

    Observe que [tex] \textcolor{#00CC00}{S_2}[/tex] é também a área da região limitada pelo segmento [tex]\overline{CB}[/tex] e pelo arco [tex]\stackrel{\frown}{CB}.[/tex]

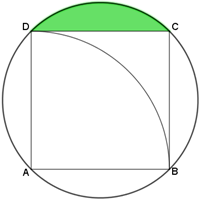
Finalmente, veja que a área [tex]S[/tex] da região colorida de amarelo é a soma da área [tex] \textcolor{#FF9900}{S_1}[/tex] com duas vezes a área [tex] \textcolor{#00CC00}{S_2}[/tex]. Dessa forma:

[tex]\qquad S= \textcolor{#FF9900}{S_1}+2 \cdot \textcolor{#00CC00}{S_2}= \textcolor{#FF9900}{4-\pi}+2 \cdot \textcolor{#00CC00}{\dfrac{\pi-2}{2}}=4-\pi+\pi-2=2\,cm^2.[/tex]
Portanto, a área da região colorida de amarelo é [tex]~\fcolorbox{black}{#e8e8e8}{$2\,cm^2$}\, .[/tex]

Solução elaborada pelos Moderadores do Blog.

Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo.
Você pode abrir o arquivo diretamente no seu navegador (Chrome, Edge, Firefox, Safari, entre outros), mas também pode utilizar o software gratuito Adobe Acrobat Reader.
Caso o dispositivo que você está utilizando não tenha o Acrobat Reader instalado, é só clicar AQUI para fazer o download adequado ao seu dispositivo.

Link permanente para este artigo: http://clubes.obmep.org.br/blog/problema-para-ajudar-na-escola-uma-area-amarela/