✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
(FGV-SP, 2007 – Adaptado) No triângulo [tex]ABC[/tex] cujos lados [tex]\overline{AB}[/tex], [tex]\overline{BC}[/tex] e [tex]\overline{AC}[/tex] medem [tex]8~cm[/tex], [tex]7~cm[/tex], [tex]6~cm[/tex], respectivamente, o lado [tex]\overline{BC}[/tex] foi prolongado até o ponto [tex]D[/tex], de modo que os ângulos [tex]A\hat{B}C[/tex] e [tex]C\hat{A}D[/tex] ficassem com a mesma medida.
Determine o perímetro do triângulo [tex]ABD[/tex].
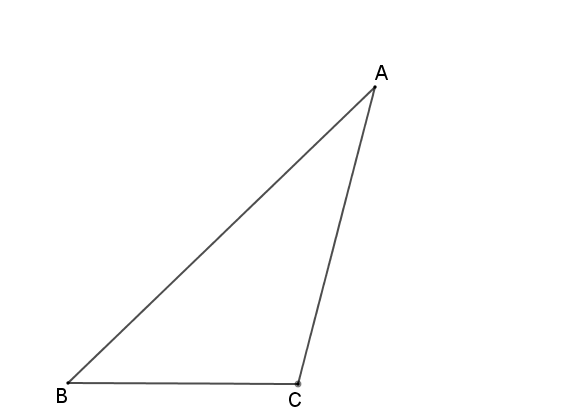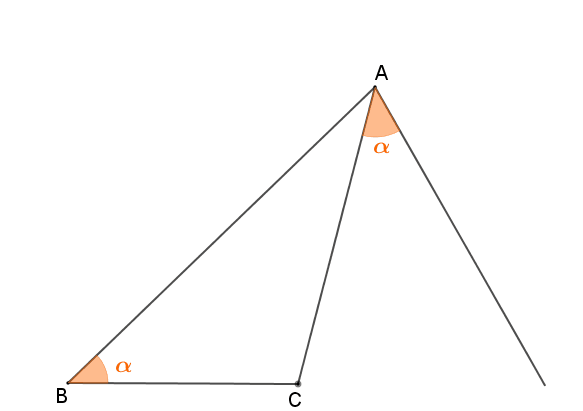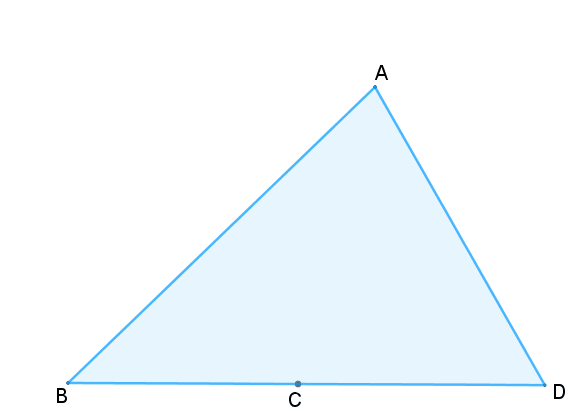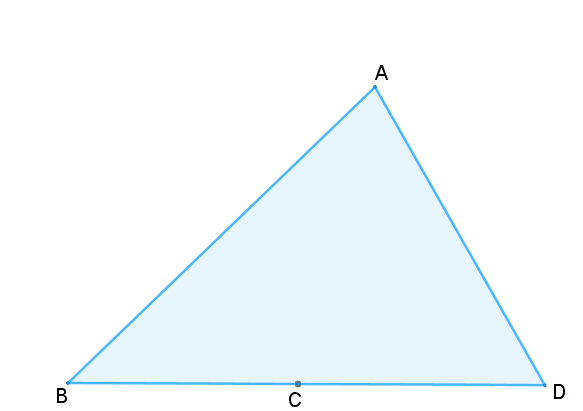Figura não proporcional aos dados do problema
Lembretes
(1) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
(2) Em triângulos semelhantes, os lados correspondentes são proporcionais.
(Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog!)
(3) Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY.[/tex]
Solução
Vamos supor que:
- [tex]a\;[/tex] e [tex]\;c[/tex] sejam as medidas, em centímetros, dos segmentos [tex]\overline{CD}\;[/tex] e [tex]\; \overline{AD}[/tex] e
- [tex]\alpha[/tex] seja a medida dos ângulos [tex]A\hat{B}C[/tex] e [tex]C\hat{A}D\,.[/tex]
Assim, ficamos com a figura mostrada a seguir.
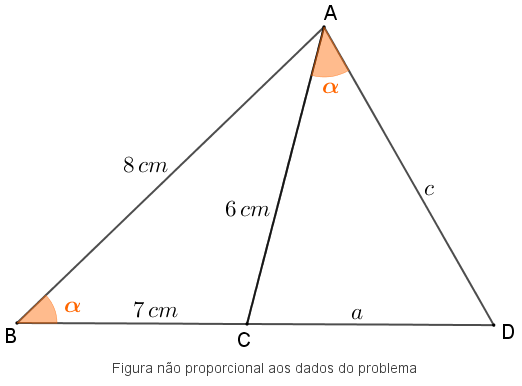
Vamos olhar para os triângulos [tex] DAB[/tex] e [tex]DCA[/tex]: vemos que os ângulos [tex]A \widehat{B}C[/tex] e [tex]C \widehat{A}D[/tex] têm a mesma medida e o ângulo de vértice [tex]D[/tex] é comum aos dois triângulos. Logo [tex]DAB\;[/tex] e [tex]\;DCA[/tex] são triângulos semelhantes, segundo o Lembrete (1) .
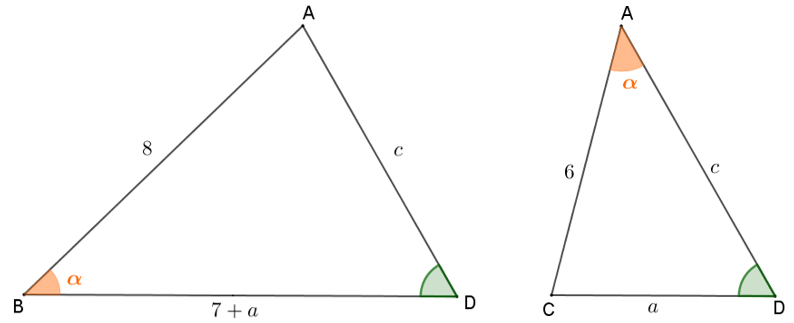
Dessa forma, pelo Lembrete (2) , temos que [tex]\boxed{\dfrac{c}{a}=\dfrac{8}{6}=\dfrac{7+a}{c}}\,[/tex], donde podemos concluir que:
|
[tex]\qquad \dfrac{c}{a}=\dfrac{8}{6}\\ \qquad \dfrac{c}{a}=\dfrac{4}{3}\\ \qquad c=\dfrac{4}{3}\cdot a\;.\qquad \textcolor{#800000}{(i)}[/tex] |
[tex]\qquad \qquad\dfrac{8}{6}=\dfrac{7+a}{c}\\ \qquad \qquad \dfrac{4}{3}=\dfrac{7+a}{c}\\ \qquad \qquad 4c=21+3a\,.\qquad \textcolor{#800000}{(ii)}[/tex] |
Agora:
|
Substituindo [tex] \textcolor{#800000}{(i)}[/tex] em [tex] \textcolor{#800000}{(ii)}[/tex], segue que: [tex]\qquad \qquad 4\cdot \dfrac{4}{3}\cdot a=21+3a [/tex] [tex]\qquad \qquad 16a=63+9a [/tex] [tex]\qquad \qquad 7a=63 [/tex] [tex]\qquad \qquad \boxed{a=9\,cm}\;. [/tex] |
Substituindo [tex]\boxed{a=9}\; [/tex] em [tex] \textcolor{#800000}{(i)}[/tex], concluímos que: [tex] \qquad \qquad c=\dfrac{4}{3}\cdot 9 [/tex] [tex] \qquad \qquad \boxed{c=12\,cm}\,. [/tex] |
Finalmente, observando que os lados do triângulo [tex]ABD[/tex] medem [tex]8\,cm[/tex], [tex]16\,cm\,[/tex] e [tex]\,12\,cm[/tex], o perímetro desse triângulo é a soma dessas três medidas, ou seja, [tex]\, \fcolorbox{black}{#eee0e5}{$8+16+12=36\,cm $}\,. [/tex]
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |