.Problema para ajudar na escola: Um retângulo ABCD e um quadrilátero MPQD

Problema
(A partir da 1ª série do E. M.) (Nível: Médio)

---

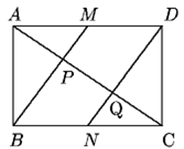
No retângulo [tex]ABCD[/tex] da figura,

• [tex]M[/tex] e [tex]N[/tex] são os pontos médios dos segmentos [tex]\overline{AD}[/tex] e [tex]\overline{BC}[/tex], respectivamente,
• [tex]P[/tex] e [tex]Q[/tex] são as respectivas interseções de [tex]\overline{AC}[/tex] com [tex]\overline{BM}[/tex] e com [tex]\overline{ND}[/tex].

Sabendo que a medida de [tex]\overline{AD}[/tex] é [tex]5 \, cm[/tex] e a de [tex]\overline{AB}[/tex] é [tex]3 \, cm[/tex], qual a área do quadrilátero [tex]MPQD?[/tex]

Solução

---

[tex]\textcolor{#800000}{(a)}[/tex] De maneira rápida poderíamos resolver o problema observando que os triângulos [tex]ABM[/tex] e [tex]DNC[/tex] são congruentes e cada um tem área igual a [tex] \, \dfrac{2,5 \times 3}{2} \, cm^2[/tex].
Por outro lado, os segmentos [tex]\overline{BM}[/tex] e [tex]\overline{ND}[/tex] são paralelos e a área do quadrilátero [tex] MPQD[/tex] é a metade da área que sobra do retângulo maior [tex]ABCD[/tex], quando eliminamos as áreas dos triângulos [tex]ABM[/tex] e [tex]DNC[/tex], que juntas valem [tex]2,5 \times 3 \, cm^2[/tex].
Assim, a área solicitada no problema é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{5 \times 3-(2,5 \times 3)}{2}=3,75 \, cm^2$} \, .[/tex]

---

---

[tex]\textcolor{#800000}{(b)}[/tex] Alguns de vocês que leram a solução acima devem ter ficado com muitíssimas dúvidas, não é?
Então, vamos fazer uma solução mais detalhada, para tentar ajudar no entendimento da solução “taquigrafada”.

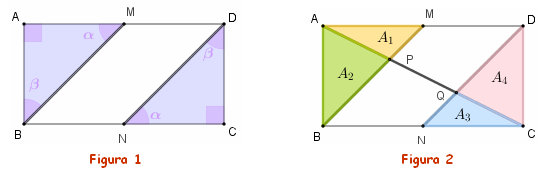
• Como os triângulos [tex]ABM[/tex] e [tex]CDN[/tex] são congruentes (são triângulos retângulos com catetos correspondentes congruentes), seus ângulos correspondentes têm as mesmas medidas, conforme indicamos na Figura 1.
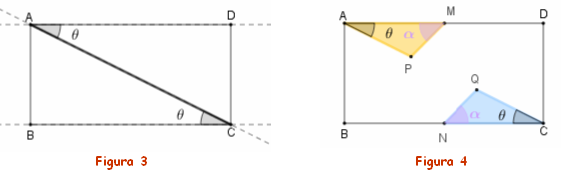
  Observe, também, que esses dois triângulos têm a mesma área; logo, temos as áreas indicadas na Figura 2 assim relacionadas: [tex]A_1+A_2=A_3+A_4[/tex]. [tex]\quad \textcolor{#800000}{(i)}[/tex]



• Observe com auxílio da Figura 3 que os ângulos [tex]B\hat{C}A[/tex] e [tex]C\hat{A}D[/tex] são alternos internos; logo, são congruentes (Se você não sabe o que são ângulos alternos internos, clique AQUI). Por outro lado, sabemos que os segmentos [tex]\overline{AM}[/tex] e [tex]\overline{NC}[/tex] têm a mesma medida.
  Dessa forma, os triângulos [tex]APM[/tex] e [tex]CQN[/tex], mostrados na Figura 4, são congruentes (caso ALA) e, portanto, as áreas [tex]A_1[/tex] e [tex]A_3[/tex] são iguais.
  Segue, então, de [tex]\textcolor{#800000}{(i)}[/tex], que [tex]A_2=A_4[/tex]. [tex]\quad \textcolor{#800000}{(ii)}[/tex]



• Observe, finalmente, que os triângulos retângulos [tex]ABC[/tex] e [tex]CDA[/tex] são também congruentes (caso [tex]LLL[/tex]) e, portanto, têm a mesma área. Dessa forma, [tex]A_1+A_6+A_4=A_2+A_5+A_3[/tex].
  Mas [tex]A_2=A_4[/tex] e [tex]A_1=A_3[/tex]; logo, [tex]A_6=A_5[/tex].

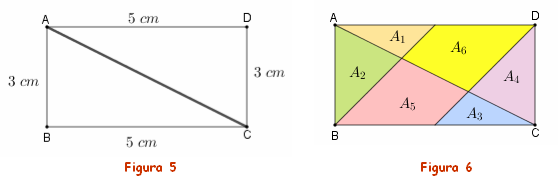
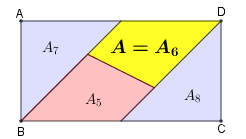
A área do retângulo [tex]ABCD[/tex] pode ser decomposta como soma das áreas [tex]A_5, \, A_6, \, A_7, \, A_8[/tex], conforme mostra a figura ao lado, sendo [tex]A=A_6[/tex] a área solicitada no problema.
Mas sabemos que:

• a área do retângulo [tex]ABCD[/tex] é [tex]3 \times 5=15 \, cm^2[/tex];
• as áreas [tex]A_7 \, [/tex] e [tex] \, A_8[/tex] são iguais a [tex]\dfrac{2,5 \times 3}{2}[/tex];

logo:
[tex]\qquad 15=A_5+A_6+A_7+A_8[/tex]
[tex]\qquad 15=A_5+A+\dfrac{2,5 \times 3}{2}+\dfrac{2,5 \times 3}{2}[/tex]
[tex]\qquad 15=A+A+2,5 \times 3[/tex]
[tex]\qquad 2A=15-2,5 \times 3[/tex]
[tex]\qquad 2A=15-7,5[/tex]
[tex]\qquad A=\dfrac{7,5}{2}[/tex]
[tex]\qquad A=3,75[/tex]
e, assim, a área solicitada no problema é [tex] \, \fcolorbox{black}{#eee0e5}{$3,75 \, cm^2$} \, .[/tex]

---

Soluções elaboradas pelos Moderadores do Blog.