✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
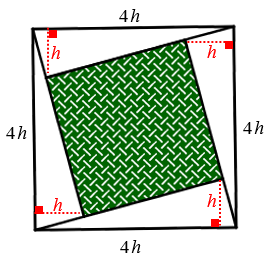
No interior de um quadrado, desenhamos quatro triângulos retângulos cujas hipotenusas são os lados do quadrado, conforme mostra a figura. Se as hipotenusas medem o quádruplo das respectivas alturas relativas a elas, determinar o quociente entre o comprimento do lado do quadrado colorido resultante da construção e o comprimento do lado do quadrado inicial.

Solução
Vamos observar os quatro triângulos retângulos construídos no interior do quadrado inicial.
Sabemos que as hipotenusas desses triângulos medem o quádruplo das respectivas alturas relativas a elas; assim, se as alturas tiverem comprimento [tex]h[/tex], as hipotenusas, que são os lados do quadrado maior, medirão [tex]4h.[/tex] Dessa forma, cada triângulo terá área [tex]\dfrac{4h\cdot h}{2}= 2h^2[/tex].
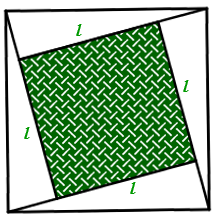
Por outro lado, a área do quadrado externo é a soma das áreas dos quatro triângulos com a área do quadrado interno. Assim, se [tex] \, l \, [/tex] for o comprimento de cada lado do quadrado interno, teremos [tex]\boxed{\left(4h\right)^2= 4\cdot 2h^2+l^2} \, .[/tex]
Então, segue que:
[tex]\quad \left(4h\right)^2= 4\cdot 2h^2+l^2[/tex]
[tex]\quad 16h^2= 8h^2+l^2 \, [/tex]
[tex]\quad 16h^2-8h^2= l^2 \, [/tex]
[tex]\quad 8h^2= l^2[/tex]
[tex]\quad \sqrt{8h^2}=\sqrt{ l^2} \, [/tex],
e como [tex]h \gt 0 \, [/tex] e [tex] \, l \gt 0[/tex], temos ainda que
[tex]\qquad \sqrt{8}\,h= l[/tex]
[tex]\qquad \boxed{l= 2\sqrt{2}\,h} \, .\quad \qquad \textcolor{#800000}{(i)}[/tex]
Dessa forma, a razão entre o comprimento do lado do quadrado colorido resultante da construção e o comprimento do lado do quadrado inicial pode ser assim calculada:
[tex]\qquad \dfrac{\text{comprimento do lado do quadrado colorido }}{\text{comprimento do lado do quadrado inicial}}=\dfrac{l}{4h}\stackrel{\textcolor{#800000}{(i)}}{=}\dfrac{2\sqrt{2}\,\cancel{h}}{4\cancel{h}}=\dfrac{\cancel{2}\sqrt{2}}{\cancel{4}}=\dfrac{\sqrt{2}}{2} \, .[/tex]
Portanto, o quociente entre o comprimento do lado do quadrado colorido resultante da construção e o comprimento do lado do quadrado inicial é [tex]\fcolorbox{black}{#eee0e5}{$ \dfrac{\sqrt{2}}{2}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
