✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.) (Nível: Muito Difícil)
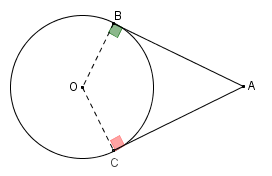
(UFMG) Observe a figura.
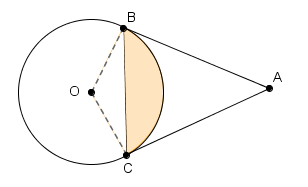
Nessa figura, [tex]OA=4\sqrt{3}[/tex], [tex]OB=2\sqrt{3} \, [/tex] e [tex] \, \overline{AB} \, [/tex] e [tex] \, \overline{AC} \, [/tex] tangenciam a circunferência de centro [tex]O[/tex] em [tex]B \, [/tex] e [tex] \, C[/tex].
Qual a área da região colorida?
Para ajudar . . .
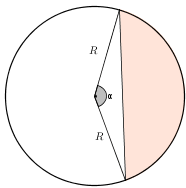
✐ Área de um segmento circular de raio [tex]R[/tex] e [tex]\alpha[/tex] radianos
[tex]\qquad \qquad \boxed{A_{segm}=\dfrac{R^{ \, 2}}{2}\left(\alpha-sen \, \alpha\right)}[/tex]
✐ Toda tangente a uma circunferência é perpendicular ao raio no ponto de tangência.
✐ Dois triângulos retângulos que tenham ordenadamente congruentes um cateto e a hipotenusa são congruentes
Solução
Observe que a região colorida da qual calcularemos a área é um segmento circular; assim, como já conhecemos o raio do círculo que define esse segmento circular, será necessário apenas determinar a medida do ângulo central [tex]\alpha[/tex] que o define.
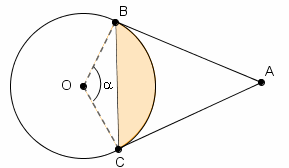
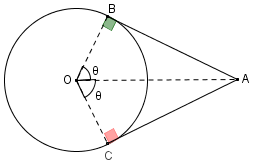
Para isso, observe inicialmente que, como “toda reta tangente à uma circunferência é perpendicular ao raio no ponto de tangência”:
- o ângulo [tex]O\widehat{B}A[/tex] é um ângulo reto;
- o ângulo [tex]O\widehat{C}A[/tex] é um ângulo reto.
Dessa forma, os triângulos [tex]ABO[/tex] e [tex]ACO[/tex] são triângulos retângulos com hipotenusas congruentes (a hipotenusa é comum aos dois) e dois catetos congruentes (cada um tem um raio como cateto); portanto [tex]ABO[/tex] e [tex]ACO[/tex] são triângulos congruentes.
|
|
Assim, para calcular [tex]\alpha[/tex], basta calcular a medida [tex]\theta[/tex] destaca na figura ao lado, já que [tex]\alpha=2\theta[/tex].
[tex]\qquad \qquad cos \, \theta=\dfrac{OB}{OA}=\dfrac{2\sqrt{3}}{4\sqrt{3}}=\dfrac{1}{2}[/tex].
Então, [tex]\theta=\dfrac{\pi}{3} \, rad[/tex] e, portanto, [tex]\boxed{\alpha=\dfrac{2\pi}{3} \, rad}[/tex]. |
Finalmente, podemos calcular a área do segmento circular determinado pela corda BC:
[tex]\qquad \begin{align*} A_{segm}&=\dfrac{R^{ \, 2}}{2}\left(\alpha-sen \, \alpha\right)\\
&=\dfrac{\left(2\sqrt{3}\right)^2}{2}\left(\dfrac{2\pi}{3}-sen \, \dfrac{2\pi}{3}\right)\\
&=6\left(\dfrac{4\pi-3\sqrt{3}}{6}\right)\\
&=4\pi-3\sqrt{3}.
\end{align*}[/tex]
Portanto, a área da região colorida é [tex]\boxed{4\pi-3\sqrt{3}}[/tex].
É comum a confusão entre dois objetos geométricos distintos: setor circular e segmento circular. Ambos dependem de uma circunferência e de um ângulo central, eles têm certa relação entre si, mas são objetos distintos.
Se você não se lembra desses dois objetos, clique no botão abaixo e aprenda um pouco mais.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |