Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
Determinar todos os valores reais de [tex]~x~[/tex] que satisfazem a seguinte condição: [tex]|4x-1|\lt |2-x|~.[/tex]

Lembretes
(1) Se [tex]a[/tex] e [tex]b[/tex] são números reais não negativos, então as afirmações [tex]\;\boxed{a \lt b}\;[/tex] e [tex]\;\boxed{a^2 \lt b^2}\;[/tex]são equivalentes:
Em símbolos: [tex]a \lt b \,\, \iff \; a^2 \lt b^2.[/tex]
(2) Se [tex]a[/tex] é um número real, então [tex]a^2=|a|^2\,.[/tex]
Solução
Como por definição de valor absoluto de um número real sabemos que [tex]|4x-1|\geqslant 0\;[/tex] e [tex]\; |2-x|\geqslant 0[/tex], o Lembrete (1) nos garante que:
[tex]\qquad \qquad |4x-1|\lt |2-x| \; \iff \; |4x-1|^2\lt |2-x|^2.\qquad \textcolor{#800000}{(i)}[/tex]
Por outro lado, sendo [tex]x[/tex] um número real, temos que [tex]4x-1\;[/tex] e [tex]\;2-x\;[/tex] são números reais. Logo, pelo Lembrete (2), temos que:
[tex]\qquad \qquad |4x-1|^2=\left(4x-1\right)^2\qquad [/tex] e [tex]\qquad |2-x|^2=\left(2-x\right)^2.\qquad \textcolor{#800000}{(ii)}[/tex]
Assim, por [tex]\textcolor{#800000}{(i)}[/tex] e [tex] \textcolor{#800000}{(ii)}[/tex] segue que
[tex]|4x-1|\lt |2-x| \; \iff \; |4x-1|^2\lt |2-x|^2 \; \iff \; \left(4x-1\right)^2\lt \left(2-x\right)^2[/tex],
e, portanto, podemos resolver a desigualdade [tex]|4x-1|\lt |2-x| [/tex], resolvendo a desigualdade [tex] \left(4x-1\right)^2\lt \left(2-x\right)^2.[/tex]
Vamos lá!
De [tex]\left(4x-1\right)^2\lt \left(2-x\right)^2[/tex] segue que:
[tex]\qquad 16x^2-8x+1\lt 4-4x+x^2[/tex]
[tex]\qquad 15x^2-4x-3\lt 0[/tex],
assim, estamos procurando números reais [tex]x[/tex] que tornem a expressão [tex] 15x^2-4x-3[/tex] negativa. Vamos, então, fazer a análise da variação de sinal dessa expressão.
Uma maneira rápida de estudarmos o sinal dessa expressão é observarmos o gráfico da função [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x)=15x^2-4x-3[/tex]. Em um plano cartesiano [tex]xOy[/tex] esse gráfico é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex] e concavidade voltada para cima. Para traçar o gráfico de [tex]\, f[/tex] e analisar a variação de sinal, vamos precisar das raízes da equação de segundo grau [tex]15x^2-4x-3=0[/tex]; são elas:
[tex]\qquad \qquad x=\dfrac{-(-4)\pm\sqrt{(-4)^2-4\cdot 15\cdot (-3)}}{2\cdot 15} [/tex]
[tex]\qquad\qquad x=\dfrac{4\pm\sqrt{196}}{30} [/tex]
[tex]\qquad\qquad x=\dfrac{4 \pm 14}{30} [/tex]
[tex]\qquad\qquad x_1=\dfrac{4+14}{30}=\dfrac{18}{30}\, \, [/tex] e [tex]\, \, x_2=\dfrac{4-14}{30}=\dfrac{-10}{30} [/tex]
[tex]\qquad\qquad \boxed{x_1=\dfrac{3}{5}}\, \, [/tex] e [tex]\, \, \boxed{x_2=-\,\dfrac{1}{3}}\,.[/tex]
Mesmo sem as coordenadas do vértice da parábola, somente sabendo que essa parábola tem concavidade voltada para cima, já temos condições de analisar a variação de sinal da expressão [tex]15x^2-4x-3=0[/tex]; observe:
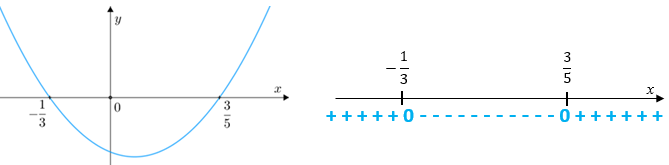
Observando os valores de [tex]x[/tex] para os quais a função [tex]f[/tex] é negativa, concluímos que a desigualdade [tex]\, |4x-1|\lt |2-x|\,[/tex] é satisfeita para valores reais de [tex]x[/tex] entre [tex]-\dfrac{1}{3}\,[/tex] e [tex]\,\dfrac{3}{5}[/tex], ou seja, [tex] \, \fcolorbox{black}{#eee0e5}{$x \in \left]-\dfrac{1}{3} \,, \,\dfrac{3}{5}\right[\,$}\,.[/tex]
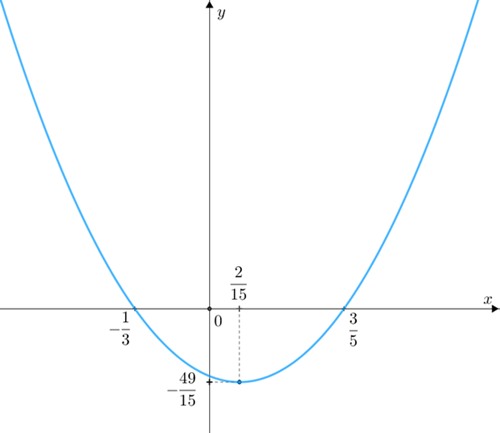
Embora não necessário, vamos calcular as coordenadas do vértice da parábola para obter um esboço melhor do gráfico da função [tex]f[/tex]. Sabemos que, se [tex](x_v,y_v)[/tex] são essas coordenadas, então:
- [tex]x_v[/tex] é a média aritmética de [tex]x_1[/tex] e [tex]x_2[/tex] e
- [tex]y_v=f(x_v)[/tex], ou ainda, [tex]y_v=\dfrac{-\left(4^2-4\cdot 15 \cdot (-3)\right)}{2\cdot 15}=-\dfrac{196}{60}=\dfrac{49}{15}[/tex].
Assim, no nosso caso:
- [tex]x_v=\dfrac{\dfrac{3}{5}-\dfrac{1}{3}}{2}=\dfrac{\dfrac{4}{15}}{2}=\dfrac{2}{15}\quad[/tex] , [tex] \quad y_v=f\left(\dfrac{2}{15}\right)=-\dfrac{49}{15}\,[/tex]
e, portanto, o vértice da parábola é o ponto [tex]V=\left(\dfrac{2}{15},-\dfrac{49}{15}\right)\,.[/tex]
Com isso, conseguimos um esboço melhorzinho do gráfico da função [tex]f\, .[/tex]
(…E o módulo nem atrapalhou muito, não é?)
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
