✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
(XX OPM, 2001 – Adaptado) No interior de um retângulo, foram desenhados dois triângulos e uma circunferência, conforme mostra a figura.
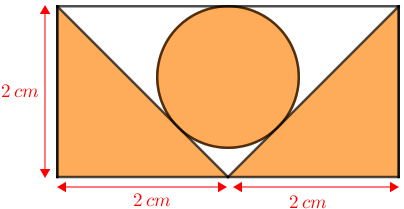
Sabendo que a circunferência tangencia os três segmentos nos quais se apoia, quanto mede a área da região colorida?
Solução
Para facilitar a solução, vamos nomear o retângulo de [tex]ABCD[/tex], o centro da circunferência de [tex]O[/tex], seu raio de [tex]r[/tex] e os seus pontos de tangência com relação aos segmentos nos quais ela se apoia de [tex]F[/tex], [tex]G[/tex] e [tex]H[/tex], conforme indica a figura abaixo.
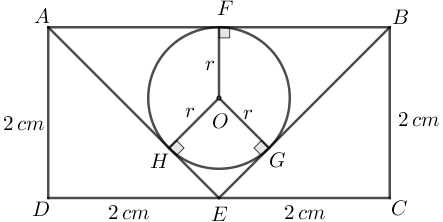
A área da região colorida é a soma de três áreas: as áreas dos triângulos [tex]AED[/tex] e [tex]BEC[/tex] e a área do círculo de centro em [tex]O[/tex] e raio [tex]r.[/tex]
► Áreas dos triângulos [tex]AED[/tex] e [tex]BEC[/tex]
As áreas dos triângulos são iguais e podem ser calculadas sem muita complicação, já que os triângulos em questão são triângulos retângulos e, portanto, seus catetos podem ser considerados como base e altura. Assim:
- [tex]A_{ADE}=A_{BEC}=\dfrac{2 \times 2}{2}=2 \, cm^2 \, .\qquad \textcolor{#800000}{(i)}[/tex]
► Área do círculo
Aqui teremos um pouco mais de trabalho…
- Observe, inicialmente, que [tex]H\hat EG[/tex] é um ângulo reto.
- Observe também que o quadrilátero [tex]OGEH[/tex] é um quadrado.
Com efeito, note que os triângulos retângulos [tex]AED[/tex] e [tex]BEC[/tex] são isósceles; logo, os ângulos das respectivas bases medem [tex]45^\circ[/tex] cada. Com isso, a medida do ângulo [tex]A\hat EB[/tex] é [tex]\boxed{180^\circ-45^\circ-45^\circ=90^\circ} \, .[/tex]
Com efeito, note que os ângulos [tex]O\hat GE[/tex], [tex]G\hat EH[/tex] e [tex]E\hat HO[/tex] medem [tex]90^\circ[/tex] cada; logo, o quarto ângulo interno do quadrilátero, [tex]H\hat {O}G[/tex], também mede [tex]90^\circ[/tex] e, portanto, o quadrilátero [tex]OGEH[/tex] é um retângulo. Mas é um retângulo com dois lados adjacentes com o mesmo comprimento [tex]r[/tex]; logo, é um quadrado, de fato.
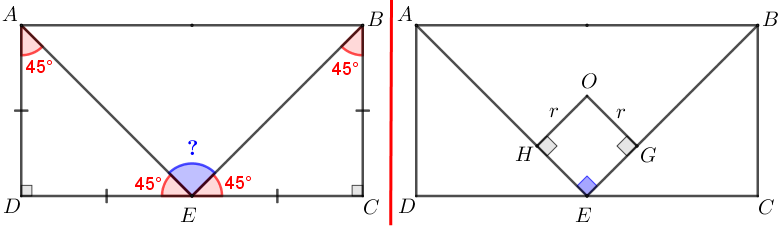
Podemos então fazer um desenho mais completo da figura fornecida pelo problema e obter o valor de [tex]r[/tex], que permitirá obtermos a área do círculo que compõe a região colorida.
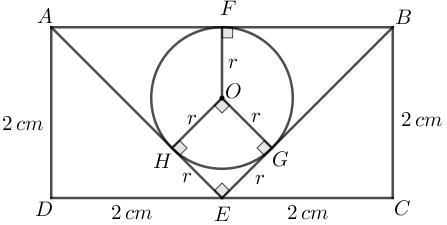
Vamos aplicar o Teorema de Pitágoras ao triângulo retângulo [tex]OGE.[/tex] Para isso, observe que o comprimento em [tex] \, cm[/tex] do segmento [tex]OE[/tex], hipotenusa do triângulo, é [tex]2-r[/tex] e assim:
[tex]\qquad \left(2-r\right)^2=r^2+r^2[/tex]
[tex]\qquad 4-4r+r^2=2r^2[/tex]
[tex]\qquad r^2+4r-4=0. \qquad \textcolor{#800000}{(ii)}[/tex]
Resolvendo a equação do segundo grau [tex]\textcolor{#800000}{(ii)}[/tex] obtemos que:
[tex]\qquad r=\dfrac{-4\pm\sqrt{16+16}}{2}=\dfrac{-4\pm\sqrt{32}}{2}[/tex]
[tex]\qquad r=\dfrac{-4\pm 4\sqrt{2}}{2}=-2\pm 2\sqrt{2}.[/tex]
Mas [tex]r[/tex] é o comprimento de um segmento e, portanto, maior do que zero. Assim, [tex]r= 2\sqrt{2}-2 \, \, cm.[/tex]
Dessa forma, a área do círculo de centro em [tex]O[/tex] e raio [tex]r[/tex] é
- [tex]A_{circ}=\pi \left( 2\sqrt{2}-2 \right)^2=\pi \left( 8-8\sqrt{2}+4\right)=\pi \left( 12-8\sqrt{2}\right) \, cm^2.\qquad \textcolor{#800000}{(iii)}[/tex]
► Área da região colorida
Por [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], temos que a área da região colorida pode ser assim calculada:
[tex]\qquad A_{\textcolor{#FF8C00}{ \, colorida}}=A_{ADE}+A_{BEC}+A_{circ}[/tex]
[tex]\qquad A_{\textcolor{#FF8C00}{ \, colorida}}=2+2+\pi \left( 12-8\sqrt{2}\right)[/tex]
[tex]\qquad A_{\textcolor{#FF8C00}{ \, colorida}}=4+\pi \left( 12-8\sqrt{2}\right).[/tex]
Portanto, a área da região colorida é [tex] \, \fcolorbox{black}{#eee0e5}{$ \, 4+\pi \left( 12-8\sqrt{2}\right) \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
