✏ Link do problema para dispositivos da Apple.
Problema
(XII Concurso de Primavera de Matemáticas – 2008) Na figura, vemos um cata-vento formado por quatro triângulos retângulos isósceles e um quadrado. Esse cata-vento foi desenhado no interior de um octógono cuja área mede [tex]56~cm^2[/tex], de modo que ele e o octógono ficaram com quatro vértices em comum.
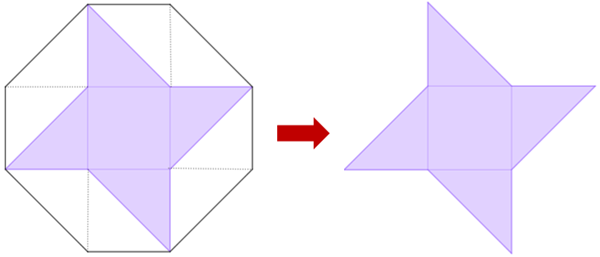
Quanto mede a área do cata-vento?
Solução 1
(Indicada a partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Inicialmente, observe que o octógono dentro do qual o cata-vento foi desenhado NÃO É REGULAR!
Como o único dado numérico é a área desse octógono, vamos decompô-lo em figuras cujas áreas nós conhecemos. Por exemplo, denotando o comprimento em centímetros de cada lado do quadrado central por [tex]l[/tex], podemos decompor o octógono em cinco quadrados de lados com comprimentos [tex]l[/tex] e quatro triângulos retângulos isósceles cujos catetos medem [tex]l[/tex] também.
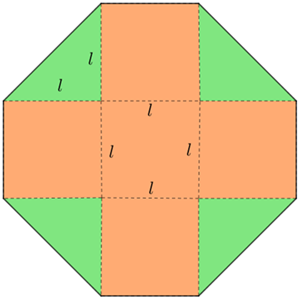 Agora, observe que:
Agora, observe que:
- a medida da área de cada quadrado é [tex]\textcolor{#FF6600}{A_q=l^2\;cm^2}[/tex];
- a medida da área de cada triângulo é [tex]\textcolor{#00CC00}{A_t=\dfrac{l^2}{2};cm^2}[/tex].
Como a área do octógono mede [tex]56~cm^2[/tex], segue que:
[tex]\qquad \qquad 56= 5 \cdot \textcolor{#FF6600}{A_q}+4\cdot \textcolor{#00CC00}{A_t} [/tex]
[tex]\qquad \qquad 56= 5 \cdot \textcolor{#FF6600}{l^2}+4\cdot \textcolor{#00CC00}{\dfrac{l^2}{2}} [/tex]
[tex]\qquad \qquad 56= 5 \cdot l^2+2\cdot l^2 [/tex]
[tex]\qquad \qquad 56= 7 \cdot l^2 [/tex]
[tex]\qquad \qquad \boxed{8= l^2} \qquad \textcolor{#800000}{(i)}[/tex]
[tex]\qquad \qquad \boxed{l= \sqrt{8}\, cm}\;. [/tex]
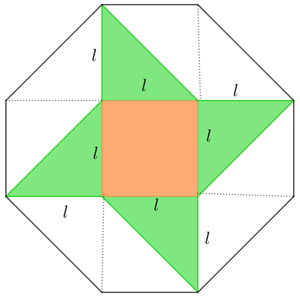
Observe agora que podemos decompor o cata-vento em um quadrado de lados com comprimentos [tex]l[/tex] e quatro triângulos retângulos isósceles cujos catetos medem [tex]l[/tex]; dessa forma, a medida [tex]\textcolor{#7D7DFF}{A_c}[/tex] da área do cata-vento pode ser assim calculada:
[tex]\qquad \qquad \textcolor{#7D7DFF}{A_c}=4\cdot\textcolor{#00CC00}{A_t}+\textcolor{#FF6600}{A_q} [/tex]
[tex]\qquad \qquad \textcolor{#7D7DFF}{A_c}=4\cdot\textcolor{#00CC00}{\dfrac{l^2}{2}}+\textcolor{#FF6600}{l^2} [/tex]
[tex]\qquad \qquad \textcolor{#7D7DFF}{A_c}=2\cdot l^2+l^2[/tex]
[tex]\qquad \qquad \textcolor{#7D7DFF}{A_c}\stackrel{\textcolor{#800000}{(i)}}{=}3\cdot 8[/tex]
[tex]\qquad \qquad \textcolor{#7D7DFF}{A_c=24\, cm^2}\,.[/tex]
Portanto, a medida da área do cata-vento é [tex]\, \fcolorbox{black}{#e3e3ff}{$\, 24\, cm^2\,$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
(Indicada a partir do 8º ano do E. F. – Nível de dificuldade: Médio)
Nesta segunda solução, vamos decompor o octógono em quatorze triângulos retângulos isósceles com catetos medido [tex]l\, cm[/tex] cada. Observe que, neste caso, a área do cata-vento corresponde à área de seis triângulos.
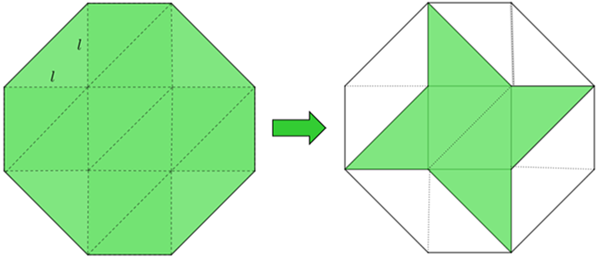
Dessa forma, se denotarmos por [tex]A_o[/tex], [tex]A_c[/tex] e [tex]A_t[/tex] as medidas das áreas do octógono, do cata-vento e de um triângulo, respectivamente, temos que [tex]\dfrac{A_c}{A_o}=\dfrac{6\cdot A_t}{14 \cdot A_t}=\dfrac{3}{7}[/tex], ou seja, a medida da área do triângulo corresponde a três sétimos da medida da área do octógono. Assim:
[tex]\qquad A_c=\dfrac{3}{7}\cdot {A_o}[/tex]
[tex]\qquad A_c=\dfrac{3}{7}\cdot 56[/tex]
[tex]\qquad A_c=3\cdot 8=24.[/tex]
Logo, a medida da área do cata-vento é [tex]\, \fcolorbox{black}{#dfd}{$\, 24\, cm^2\,$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
