✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
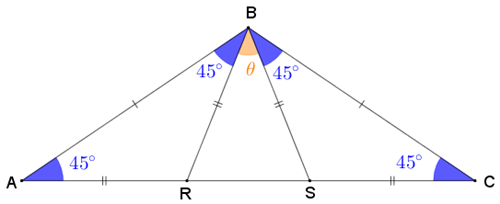
A partir de três triângulos isósceles queremos construir um grande triângulo isósceles conforme mostrado na figura.
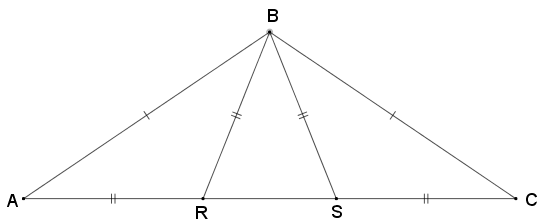
(a) Se [tex]\alpha=38^\circ[/tex], qual será o valor, em graus, de [tex]\theta[/tex]?
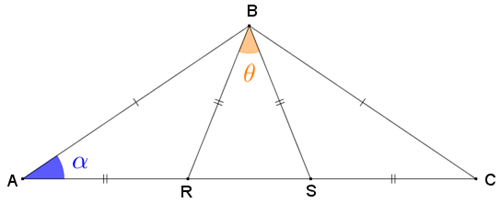
(b) A construção é possível com [tex]\alpha=45^\circ[/tex]?
(c) E com [tex]\alpha=48^\circ[/tex]?

Lembretes
(1) Os ângulos da base de um triângulo isósceles têm a mesma medida. (Se precisar, veja o finalzinho desta página.)
(2) A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex]. (Se precisar, visite esta página.)
Solução
(a) Observe, inicialmente, que o triângulo [tex]ABR[/tex] é isósceles. Como [tex]\alpha=38^\circ[/tex], utilizando os Lembretes (1) e (2), nesta ordem, obtemos que:
- a medida do ângulo [tex]A\hat{B}R[/tex] é [tex]38^\circ[/tex]
- e a medida do ângulo [tex]B\hat{R}A[/tex] é dada por [tex]180^\circ-38^\circ-38^\circ=104^\circ.[/tex]
Observe, agora, o triângulo [tex]ABC[/tex] e veja que ele é isósceles. Assim, utilizando o Lembrete (1), segue que:
- a medida do ângulo [tex]B\hat{C}S[/tex] é [tex]38^\circ.[/tex]
Observe, também, que o triângulo [tex]BSC[/tex] é isósceles; portanto, utilizando os Lembretes (1) e (2), nesta ordem, vem que:
- a medida do ângulo [tex]C\hat{B}S[/tex] é [tex]38^\circ[/tex]
- e a medida do ângulo [tex]C\hat{S}B[/tex] é dada por [tex]180^\circ-38^\circ-38^\circ=104^\circ.[/tex]
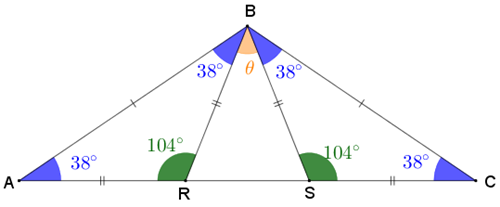
Finalmente, observe o triângulo [tex]BSR[/tex] e veja que:
- os ângulos [tex]B\hat{R}S[/tex] e [tex]B\hat{S}R[/tex] são suplementares de [tex]104^\circ[/tex]; logo, a medida de cada um é [tex]180^\circ-104^\circ=76^\circ.[/tex]
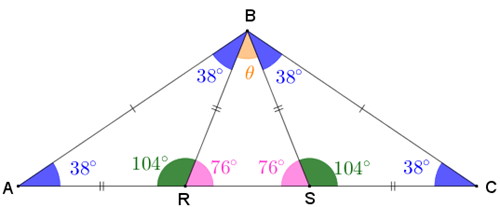
Dessa forma, utilizando uma vez mais o Lembrete (2), obtemos que [tex] \, \fcolorbox{black}{#FFE4B5}{$\theta=180^\circ-76^\circ-76^\circ=28^\circ$} \, .[/tex]
(b) Para este item, como [tex]\alpha=45^\circ[/tex] e o triângulo [tex]ABC[/tex] é isósceles, podemos utilizar o Lembrete (1) e concluir que:
- a medida do ângulo [tex]B\hat{C}A[/tex] é [tex]45^\circ.[/tex]
Observe agora que, como os triângulos [tex]ABR[/tex] e [tex]CBS[/tex] são isósceles, utilizando novamente o Lembrete (1), segue que:
- os ângulos [tex]A\hat{B}R[/tex] e [tex]C\hat{B}S[/tex] têm medidas [tex]45^\circ.[/tex]
Mas o Lembrete (2) aplicado no triângulo [tex]ABC[/tex] implica que
- [tex]4\times 45^\circ+\theta=180^\circ \, [/tex],
e com isso [tex]\theta=0^\circ \, [/tex] ou seja os pontos [tex]R \, [/tex] e [tex] \, S[/tex] são iguais e não temos, portanto, o terceiro triângulo interno [tex]RSB \, .[/tex]
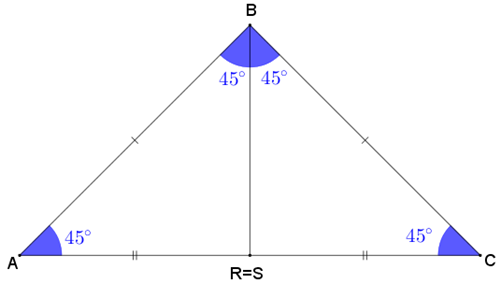
Assim, se [tex]\alpha=45^\circ[/tex], a construção de um triângulo isósceles grande a partir de três triângulos também isósceles não é possível.
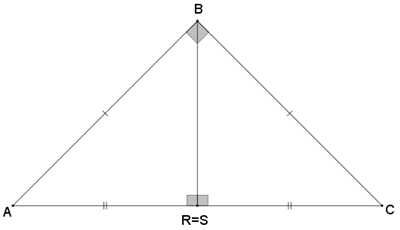
Observe que, no caso do triângulo isósceles externo formado por apenas dois triângulos isósceles, particularmente teremos os três triângulos retângulos.
(c) Neste item, temos [tex]\alpha=48^\circ[/tex]. Como os triângulos [tex]ABC[/tex], [tex]ABR[/tex] e [tex]CBS[/tex] são isósceles, podemos utilizar o Lembrete (1) e concluir que:
- a medida do ângulo [tex]B\hat{C}A[/tex] é [tex]48^\circ.[/tex]
- os ângulos [tex]A\hat{B}R[/tex] e [tex]C\hat{B}S[/tex] têm medidas [tex]48^\circ.[/tex]
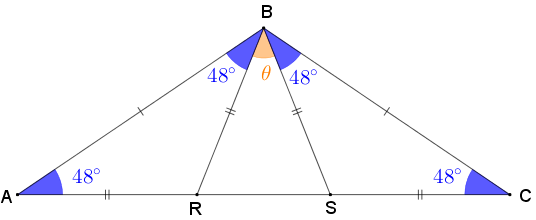
Veja que o Lembrete (2) aplicado no triângulo [tex]ABC[/tex] implica que
- [tex]180^\circ \, =4\times 48^\circ+\theta=192^\circ+\theta[/tex],
o que é impossível, já que [tex]\theta\gt 0^\circ[/tex].
Assim, sequer conseguimos definir o triângulo [tex]ABC[/tex] e, portanto, a construção proposta não é possível, se [tex]\alpha=48^\circ.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
