✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M.- Nível de dificuldade: Muito Difícil)
(ITA, 2007) Os conjuntos de números reais [tex]A, B\,[/tex] e [tex]\,C[/tex] são assim definidos:
[tex]\quad A \cup B \cup C =\left\{x \in \mathbb{R} \text{ tais que } x^2+x \geqslant 2 \right\};[/tex]
[tex]\quad \qquad A \cup B =\left\{x \in \mathbb{R} \text{ tais que } 8^{-x}-3\cdot 4^{-x}-2^{2-x} \gt 0\right\};[/tex]
[tex] \quad \qquad A \cap C =\left\{x \in \mathbb{R} \text{ tais que } log\left(x+4 \right)\leqslant 0\right\};[/tex]
[tex]\quad \qquad B \cap C =\left\{x \in \mathbb{R} \text{ tais que } 0 \leqslant 2x+7 \lt 2 \right\}.[/tex]
Determine [tex]\,C[/tex] .
Solução
Inicialmente, observe que não temos uma definição direta do conjunto [tex]\,C[/tex], precisaremos utilizar os conjuntos definidos no problema e obter [tex]\,C[/tex] a partir de operações entre conjuntos.
Observando o diagrama de Venn abaixo, vemos que
- [tex] \left[\left(A \cup B \cup C\right)-\left(A \cup B\right)\right]\cup \left[ \left(A \cap C\right) \cup \left( B \cap C\right)\right]=C[/tex].
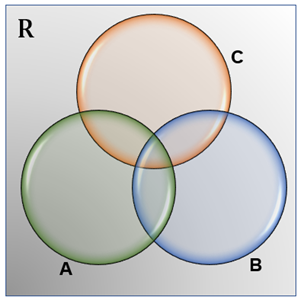
Ingenuamente podemos entender essa igualdade observando que ao fazermos a diferença [tex]\left(A \cup B \cup C\right)-\left(A \cup B\right)[/tex], apagamos de [tex]C[/tex] os elementos que também pertencem a [tex]A[/tex] e a [tex]B[/tex]; mas com a união das interseções [tex] A \cap C[/tex] e [tex]B \cap C[/tex] trouxemos de volta para [tex]C[/tex] os elementos de [tex]A[/tex] que pertencem a [tex]C[/tex] e também os elementos de [tex]B[/tex] que pertencem a [tex]C.[/tex]
Dessa forma, precisamos determinar, de fato, os conjuntos [tex]A \cup B \cup C[/tex], [tex]A \cup B[/tex], [tex] A \cap C[/tex] e [tex]B \cap C[/tex]; e, para isso, vamos, a princípio, analisar separadamente as desigualdades que os definem.
-
[tex] \textcolor{#800000}{(i)}\;\boxed{x^2+x \geqslant 2} [/tex]
Note que a desigualdade [tex] \boxed{x^2+x \geqslant 2} [/tex] é equivalente à desigualdade [tex] \boxed{x^2+x-2 \geqslant 0} [/tex] e para resolver esta segunda desigualdade em [tex]\mathbb{R}[/tex] precisamos procurar números reais [tex]x[/tex] que tornem a expressão [tex] x^2+x-2[/tex] não negativa. Para tal vamos fazer a análise da variação de sinal dessa expressão.
Uma maneira rápida de estudarmos o sinal dessa expressão é observarmos o gráfico da função [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x)=x^2+x-2[/tex]. Em um plano cartesiano [tex]xOy[/tex] esse gráfico é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex] e concavidade voltada para cima. Para traçar o gráfico de [tex]\, f[/tex] e analisar a variação de sinal, vamos precisar das raízes da equação de segundo grau [tex]x^2+x-2=0[/tex]; são elas:
[tex]\qquad \qquad x=\dfrac{-1\pm\sqrt{1^2-4\cdot 1\cdot (-2)}}{2\cdot 1}=\dfrac{-1\pm\sqrt{9}}{2}=\dfrac{-1\pm3}{2}[/tex]
[tex]\qquad\qquad \boxed{x_1=\dfrac{2}{2}=1}\, \, [/tex] e [tex]\, \, \boxed{x_2=-\,\dfrac{4}{2}=-2}\,.[/tex]
Mesmo sem as coordenadas do vértice da parábola, somente sabendo que essa parábola tem concavidade voltada para cima, já temos condições de analisar a variação de sinal da expressão [tex]x^2+x-2[/tex]; observe:
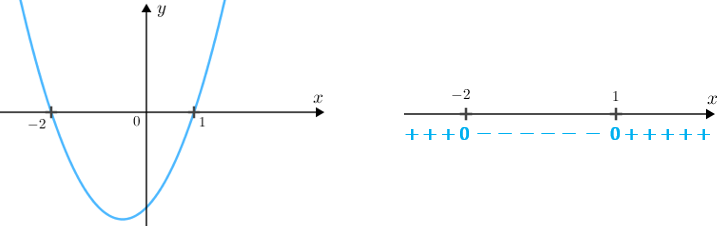
Observando os valores de [tex]x[/tex] para os quais a função [tex]f[/tex] é não negativa, concluímos que a desigualdade [tex]x^2+x \geqslant 2[/tex], e consequentemente [tex]x^2+x-2 \geqslant 0[/tex], é satisfeita para valores reais de [tex]x[/tex] tais que [tex]\, \fcolorbox{black}{#BEEDFF}{$ x\leqslant -2$}[/tex] ou [tex]\, \fcolorbox{black}{#BEEDFF}{$ x\geqslant 1$}\,.[/tex]
[tex] \textcolor{#800000}{(ii)}\;\boxed{8^{-x}-3\cdot 4^{-x}-2^{2-x} \gt 0}[/tex]
Iniciamos este caso, observando a seguinte sequência de desigualdades equivalentes:
[tex]\qquad 8^{-x}-3\cdot 4^{-x}-2^{2-x} \gt 0 \iff \left(2^3\right)^{-x}-3\cdot \left(2^2\right)^{-x}-2^2\cdot 2^{-x} \gt 0 \iff\\
\qquad \iff \left(2^{-x}\right)^3-3\cdot \left(2^{-x}\right)^2-2^2\cdot \left(2^{-x}\right) \gt 0 \iff \\
\qquad \iff \left(2^{-x}\right)\left[\left(2^{-x}\right)^2-3\cdot \left(2^{-x}\right)-4\right] \gt 0\,. [/tex]
Como [tex]\left(2^{-x}\right) \gt 0[/tex], a sequência de desigualdades finaliza assim:
[tex]\qquad 8^{-x}-3\cdot 4^{-x}-2^{2-x} \gt 0 \iff \cdots \iff\\
\qquad \iff \left(2^{-x}\right)\left[\left(2^{-x}\right)^2-3\cdot \left(2^{-x}\right)-4\right] \gt 0 \iff \left(2^{-x}\right)^2-3\cdot \left(2^{-x}\right)-4 \gt 0.[/tex]
Portanto, como as desigualdades [tex]\boxed{8^{-x}-3\cdot 4^{-x}-2^{2-x} \gt 0}[/tex] e [tex]\boxed{ \left(2^{-x}\right)^2-3\cdot \left(2^{-x}\right)-4 \gt 0}[/tex] são equivalentes, vamos resolver a segunda.
Perceba que se fizermos [tex]z= 2^{-x}[/tex] a desigualdade exponencial [tex] \left(2^{-x}\right)^2-3\cdot \left(2^{-x}\right)-4 \gt 0[/tex] se transforma na desigualdade do segundo grau [tex] z^2-3z-4 \gt 0[/tex], que pode ser resolvida fazendo-se a análise de sinal da expressão [tex] z^2-3z-4\,.[/tex]
Aqui vamos analisar a variação de sinal da função [tex]g:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]g(z)=z^2-3z-4 [/tex] para determinar para quais valores de [tex]z[/tex] a função [tex]g[/tex] é positiva. O gráfico de [tex]g[/tex] em um plano cartesiano [tex]zOy[/tex] é uma parábola com diretriz paralela ao eixo [tex]Oz[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex] e concavidade voltada para cima. Para traçar o gráfico de [tex]\,g[/tex] vamos encontrar as raízes da equação de segundo grau [tex]z^2-3z-4=0[/tex]:
[tex]\qquad \qquad z=\dfrac{-(-3)\pm\sqrt{(-3)^2-4\cdot 1\cdot (-4)}}{2\cdot 1}=\dfrac{3\pm\sqrt{25}}{2}=\dfrac{3\pm 5}{2}[/tex]
[tex]\qquad\qquad \boxed{z_1=\dfrac{8}{2}=4}\, \, [/tex] e [tex]\, \, \boxed{z_2=-\,\dfrac{2}{2}=-1}\,.[/tex]
Novamente, mesmo sem as coordenadas do vértice da parábola, somente sabendo que ela tem concavidade voltada para cima, já temos condições de analisar a variação de sinal da expressão [tex]z^2-3z-4[/tex]; observe:
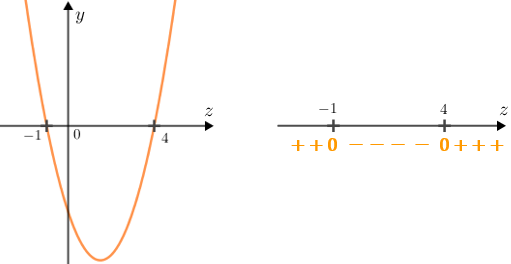
Observando os valores de [tex]z[/tex] para os quais a função [tex]g[/tex] é positiva, concluímos que a desigualdade [tex] z^2-3z-4 \gt 0[/tex] é satisfeita para valores reais de [tex]z[/tex] tais que [tex]\, z\lt -1[/tex] ou [tex]\, z\gt 4 \, .[/tex]
Mas [tex]z= 2^{-x}[/tex], assim as desigualdades equivalentes [tex]\boxed{8^{-x}-3\cdot 4^{-x}-2^{2-x} \gt 0}[/tex] e [tex]\boxed{ \left(2^{-x}\right)^2-3\cdot \left(2^{-x}\right)-4 \gt 0}[/tex] são satisfeitas para valores de [tex]x[/tex] tais que [tex]\, 2^{-x}\lt -1[/tex] ou [tex]\, 2^{-x}\gt 4 \, .[/tex]
Mas observe que [tex] 2^{-x} \gt 0[/tex], logo a condição[tex]\, 2^{-x}\lt -1 [/tex] não ocorre. Da segunda condição, segue que:
[tex]\qquad \qquad 2^{-x}\gt 4 \iff 2^{-x}\gt 2^2 \iff -x \gt 2 \iff x \lt -2[/tex],
e assim a desigualdade [tex]\boxed{8^{-x}-3\cdot 4^{-x}-2^{2-x} \gt 0}[/tex] é satisfeita para valores reais de [tex]x[/tex] tais que [tex]\, \fcolorbox{black}{#FFDA71}{$ x\lt-2$}\, .[/tex]
[tex] \textcolor{#800000}{(iii)}\;\boxed{ log\left(x+4 \right)\leqslant 0}[/tex]
Aqui, faremos [tex]x+4=t[/tex] e analisaremos a variação de sinal da função [tex]h:]0,+\infty [\rightarrow \mathbb{R}[/tex] dada por [tex]h(t)=log(t).[/tex]
O gráfico de [tex]h[/tex] aparece no lado esquerdo da figura abaixo e a variação de sinal da função [tex]h[/tex] aparece do lado direito.
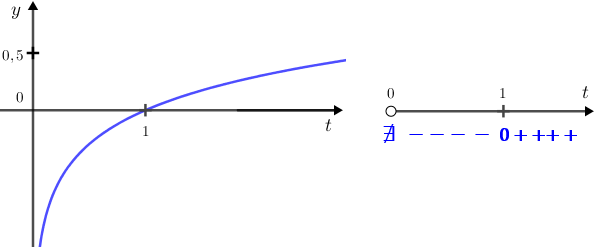
Observando os valores de [tex]t[/tex] para os quais a função [tex]h[/tex] é não positiva, concluímos que a desigualdade [tex]log(t) \leqslant 0[/tex] é satisfeita para valores reais de [tex]t[/tex] tais que [tex]0 \lt t\leqslant 1[/tex]. Assim, como [tex]t=x+4[/tex], concluímos que [tex] \boxed{ log\left(x+4 \right)\leqslant 0}[/tex] para valores reais de [tex]x[/tex] tais que [tex]0 \lt x+4 \leqslant 1[/tex], ou seja valores reais de [tex]x[/tex] tais que [tex]\, \fcolorbox{black}{#ddf}{$-4 \lt x \leqslant -3\,$}\,.[/tex]
[tex] \textcolor{#800000}{(iv)}\;\boxed{0 \leqslant 2x+7 \lt 2 }[/tex]
Para esta última desigualdade não faremos gráfico; apenas fazendo manipulações algébricas determinaremos os valores de [tex]x[/tex] que nos interessam. Observe esta sequência de desigualdades equivalentes:
[tex] \qquad \qquad 0 \leqslant 2x+7 \lt 2 \iff -7 \leqslant 2x \lt -5\iff -\dfrac{7}{2} \leqslant x \lt -\dfrac{5}{2}\,.[/tex]
Assim, vemos que [tex] \boxed{ 0 \leqslant 2x+7 \lt 2}[/tex] para valores reais de [tex]x[/tex] tais que [tex]\, \fcolorbox{black}{#d8dee4}{$-\dfrac{7}{2} \leqslant x \lt -\dfrac{5}{2} \,$}\,.[/tex]
Dessa forma, temos que:
[tex]\quad \textcolor{#0099ff}{A \cup B \cup C} =\left\{x \in \mathbb{R} \text{ tais que } \fcolorbox{black}{#BEEDFF}{$ x\leqslant -2$} \text{ ou } \fcolorbox{black}{#BEEDFF}{$ x\geqslant 1$} \right\};[/tex]
[tex]\quad \qquad \textcolor{#ff6600}{A \cup B} =\left\{x \in \mathbb{R} \text{ tais que } \fcolorbox{black}{#FFDA71}{$ x\lt-2$} \right\};[/tex]
[tex] \quad \qquad \textcolor{#0000ff}{A \cap C} =\left\{x \in \mathbb{R} \text{ tais que } \fcolorbox{black}{#ddf}{$-4 \lt x \leqslant -3\,$} \right\};[/tex]
[tex]\quad \qquad \textcolor{#6a8198}{B \cap C} =\left\{x \in \mathbb{R} \text{ tais que } \fcolorbox{black}{#d8dee4}{$-\frac{7}{2} \leqslant x \lt -\frac{5}{2} \,$} \right\}.[/tex]
Lembrando que [tex] \left[\left(A \cup B \cup C\right)-\left(A \cup B\right)\right]\cup \left[ \left(A \cap C\right) \cup \left( B \cap C\right)\right]=C[/tex], vamos visualizar juntos os quatro conjuntos.

Observe que:
- [tex] \left(A \cup B \cup C\right)-\left(A \cup B\right)=\left\{x \in \mathbb{R} \text{ tais que } x=-2 \text{ ou } x\geqslant 1 \right\}=\{-2\}\cup [1,+\infty[[/tex]
- [tex] \left(A \cap C\right) \cup \left( B \cap C\right)=\left\{x \in \mathbb{R} \text{ tais que } -4 \lt x \lt -\dfrac{5}{2} \right\}=\left]-4,-\dfrac{5}{2}\right[[/tex]


Fazendo a união desses dois conjuntos, concluímos, finalmente, que:
[tex] \qquad \qquad \fcolorbox{black}{#eee0e5}{$\,C=\left\{x \in \mathbb{R} \text{ tais que } -4 \lt x \lt -\dfrac{5}{2} \text{ ou } x=-2 \text{ ou } x\geqslant 1\right\}$}\,[/tex],
ou seja,
[tex] \qquad \qquad \fcolorbox{black}{#eee0e5}{$\,C=\left]-4,-\frac{5}{2}\right[ \cup \{-2\}\cup [1,+\infty[$}\,[/tex].

Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
